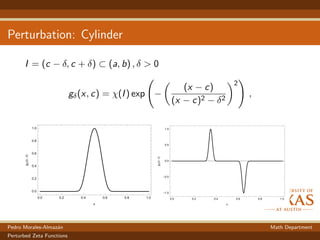
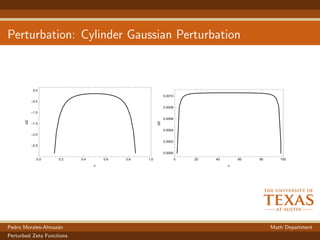
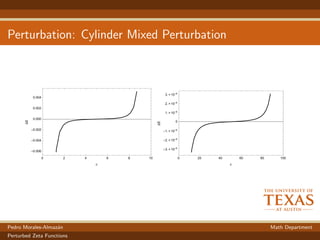
The document discusses the perturbation theory of zeta functions for surfaces of revolution, focusing on analytic continuations and their implications for Casimir energy. It examines how perturbations affect zeta functions and explores the mathematical formulation for ensuring well-defined quantities. The results indicate that Casimir energy remains unchanged by perturbations near the center while interactions at edges lead to predictable alterations in energy levels.

1. Zeta function for perturbed surfaces of revolution
Pedro Morales-Almaz´an
Department of Mathematics
The University of Texas at Austin
pmorales@math.utexas.edu
TexAMP 2016
Rice University, October 22, 2016
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

2. Zeta Function
P is a differential operator
M a d dimensional manifold
Spectral Zeta Function
ζ(s) =
λ∈σ
λ=0
λ−s
for (s) > d.
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

3. Surface of revolution
P = ∆ the
M surface of revolution y = f (x) > 0, x ∈ [a, b]
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

4. Zeta Function
Zeta Function
ζ(s) =
∞
k=−∞
1
2πi γk
dλ λ−2s d
dλ
log φk(λ; b) ,
for (s) > 1 and φk(λ; x) is a solution to the radial ODE with
initial conditions φk(λ; a) = 0 , φk(λ; a) = 1 .
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

5. Analytic Continuation
Plan
• Extend ζ(s) to the entire complex plane
• Integral representation is good for small λ (converge)
• Integral representation is bad for big λ (divergence)
• Analytic continuation (subtract the behavior for big λ)
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

6. Analytic Continuation
WKB asymptotics
ζ(s) =
sin(πs)
π
∞
0
dλ λ−2s d
dλ
log F(iλ) − ♣
+
sin(πs)
π
∞
0
dλ λ−2s d
dλ
♣
for (s) > n(♣).
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

7. Special values
Functional Determinant
Formally defined as exp(−ζ (0))Well defined since
Res ζ(0) = 0
Casimir Energy
The vacuum energy can be found by limh→0 ζ(−1/2 + h)
Not well defined!
Res ζ(−1/2) = −
1
256
f −1(a)f 2(a)
(1 + f 2(a))
+
f −1(b)f 2(b)
(1 + f 2(b))
−
1
32
f (a)
(1 + f 2(a))2
+
f (b)
(1 + f 2(b))2
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

8. Special Values: Casimir
Q: How do we find a well defined quantity? A: Perturbation
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

9. Perturbed Surface of Revolution
• Perturb the profile function
f (x) → f (x) + g(x)
• Substitute this into the previous formalism
• Calculate the variation due to the perturbation
d
d
ζ(s)
=0
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

10. Analytic Continuation
WKB asymptotics
ζ(s) =
sin(πs)
π
∞
0
dλ λ−2s d
dλ
log F(iλ) − ♣ (Finite)
+
sin(πs)
π
∞
0
dλ λ−2s d
dλ
♣ (Asymptotic)
Finite: Depend on f (x) and φk(λ; b) (More complex:???)
Asymptotic: Only depend on f (x) (Straightforward: Taylor Series)
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

11. Perturbation: Asymptotic terms
WKB asymptotics
ζ(s) =
sin(πs)
π
∞
0
dλ λ−2s d
dλ
log F(iλ) − ♣ (Finite)
+
sin(πs)
π
∞
0
dλ λ−2s d
dλ
♣ (Asymptotic)
• ♣ only depends on f (x), hence doing f (x) → f (x) + g(x)
• find terms up to O( 2)
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

12. Perturbation: Finite terms
WKB asymptotics
ζ(s) =
sin(πs)
π
∞
0
dλ λ−2s d
dλ
log F(iλ) − ♣ (Finite)
+
sin(πs)
π
∞
0
dλ λ−2s d
dλ
♣ (Asymptotic)
F +
f + g
f + g
−
(f + g ) (f + g )
1 + (f + g )2
F
+ 1 + f + g
2
λ2
−
k2
(f + g)2
F = 0 (O( 2
)) .
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

13. Perturbation: Finite terms
• F = φ + ˆφ (O( 2))
• ˆφ functional derivative
• φ satisfies the original radial equation
• ˆφ satisfies a non-homogeneous version of the radial equation
ˆφ +
f
f
−
(f ) (f )
1 + (f )2
ˆφ
+ 1 + f
2
λ2
−
k2
f 2
ˆφ = G .
• use variation of parameters
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

14. Perturbation: Zeta function
Zeta function
˜ζ(s) = ζ(s) + ˆζ(s) (O( 2
))
Effect of the perturbation
d
d
˜ζ(s)
=0
= ˆζ(s)
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

15. Perturbation: Casimir Energy
∆E =
d
d
ζ∆ (−1/2)
=0
= −
1
2π
b
a
dt
f (t)
(f (t)2 + 1)3/2
g(t)
−
ζR (−2)
π
b
a
dt
f (t)f (t) + 2f (t)2
+ 2
f (t)3 (f (t)2 + 1)3/2
g(t)
+
1
16
b
a
dt
2f (t)3
f (t)2
+ 1 + f (t)f (t) 5f (t)2
− 3 f (t)
f (t)3 (f (t)2 + 1)5
g(t)
−
1
π
1
0
dλ λ
d
dλ
ˆφ0(b; ıλ)
φ0(b; ıλ)
−
1
π
∞
1
dλ λ
d
dλ
ˆφ0(b; ıλ)
φ0(b; ıλ)
−
2
i=−1
λ−i
b
a
dt
∂
∂
si (t)
=0
−
2
π
∞
k=1
k
∞
0
du u
d
du
ˆφk (b; ıuk)
φk (b; ıuk)
−
2
i=−1
k−i
b
a
dt
∂
∂
wi (t)
=0
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

16. Perturbation: Cylinder
I = (c − δ, c + δ) ⊂ (a, b) , δ > 0
gδ(x, c) = χ(I) exp −
(x − c)
(x − c)2 − δ2
2
,
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

17. Perturbation: Cylinder Gaussian Perturbation
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

18. Perturbation: Cylinder Mixed Perturbation
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

19. Conclusions
• The Casimir doesn’t get affected by perturbations made near
the center
• The interaction between an edge and a positive (negative)
perturbation results in a negative (positive) change of the
Casimir Energy
• The results agree with the existing calculations for infinite
cylinders
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

20. References
• Thalia D Jeffres, Klaus Kirsten & Tianshi Lu (2012). Zeta
function on surfaces of revolution. Journal of Physics A:
Mathematical and Theoretical, 45, 345201.
• M-A., P. (2016). Casimir energy for perturbed surfaces of
revolution. International Journal of Modern Physics A, 31,
1650044.
• Fucci, G. & M-A., P. Perturbed zeta functions on warped
manifolds, Coming soon!
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions

21. Questions
email: pmorales@math.utexas.edu
twitter: @p3d40
Pedro Morales-Almaz´an Math Department
Perturbed Zeta Functions