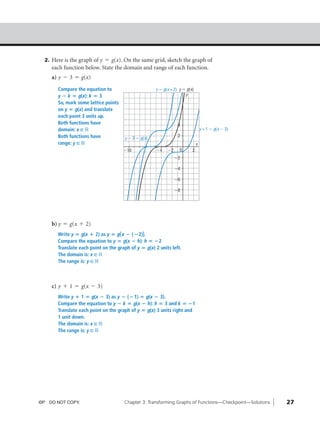
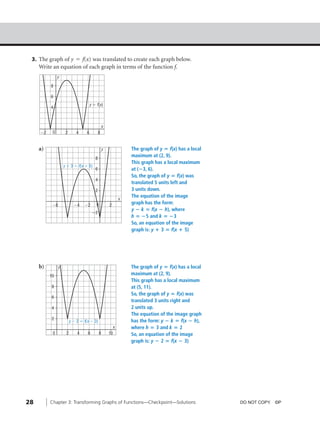
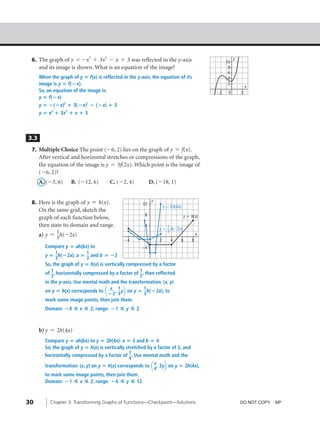
This document contains solutions to checkpoint questions about transforming graphs of functions. It includes examples of translating graphs by shifting them horizontally and vertically based on changes to the x and y variables in the function. It also contains an example of reflecting a graph across the x-axis. The questions require sketching the transformed graphs on grids and writing the equations of the transformed functions based on the given transformations.

1. 04_ch03a_pre-calculas12_wncp_solution.qxd 5/17/12 7:31 PM Page 26
Home Quit
Checkpoint: Assess Your Understanding, pages 213–218
3.1
1. Multiple Choice The graph of y ϭ Ϫ3x3 ϩ 4 is translated 4 units
right and 5 units down. What is an equation of the translation
image?
A. y = -3(x + 4)3 + 9 B. y = -3(x - 4)3 + 9
C. y = -3(x + 4)3 - 1 D. y = -3(x - 4)3 - 1
26 Chapter 3: Transforming Graphs of Functions—Checkpoint—Solutions DO NOT COPY. ©P

2. 04_ch03a_pre-calculas12_wncp_solution.qxd 5/17/12 7:31 PM Page 27
Home Quit
2. Here is the graph of y = g(x). On the same grid, sketch the graph of
each function below. State the domain and range of each function.
a) y - 3 = g(x)
Compare the equation to y ϭ g(x + 2) y ϭ g(x)
y ؊ k ‫ ؍‬g(x): k ‫3 ؍‬ y
So, mark some lattice points
on y ‫ ؍‬g(x) and translate
each point 3 units up.
Both functions have
domain: x ç ‫ޒ‬
4
y + 1 ϭ g(x Ϫ 3)
Both functions have 2
y Ϫ 3 ϭ g(x)
range: y ç ‫ޒ‬ x
Ϫ10 Ϫ4 Ϫ2 0 2
Ϫ2
Ϫ4
Ϫ6
Ϫ8
b) y = g(x + 2)
Write y ‫ ؍‬g(x ؉ 2) as y ‫ ؍‬g( x ؊ (؊2)).
Compare the equation to y ‫ ؍‬g(x ؊ h): h ‫2؊ ؍‬
Translate each point on the graph of y ‫ ؍‬g(x) 2 units left.
The domain is: x ç ‫ޒ‬
The range is: y ç ‫ޒ‬
c) y + 1 = g(x - 3)
Write y ؉ 1 ‫ ؍‬g(x ؊ 3) as y ؊ (؊1) ‫ ؍‬g(x ؊ 3).
Compare the equation to y ؊ k ‫ ؍‬g(x ؊ h): h ‫ 3 ؍‬and k ‫1؊ ؍‬
Translate each point on the graph of y ‫ ؍‬g(x) 3 units right and
1 unit down.
The domain is: x ç ‫ޒ‬
The range is: y ç ‫ޒ‬
©P DO NOT COPY. Chapter 3: Transforming Graphs of Functions—Checkpoint—Solutions 27

3. 04_ch03a_pre-calculas12_wncp_solution.qxd 5/17/12 7:31 PM Page 28
Home Quit
3. The graph of y = f(x) was translated to create each graph below.
Write an equation of each graph in terms of the function f.
y
8
6
y ϭ f(x)
4
x
Ϫ2 0 2 4 6 8
a) y The graph of y ‫ ؍‬f(x) has a local
maximum at (2, 9).
8
This graph has a local maximum
y ϩ 3 ϭ f(x ϩ 5)
6 at (؊3, 6).
So, the graph of y ‫ ؍‬f(x) was
4
translated 5 units left and
2 3 units down.
The equation of the image
x
Ϫ8 Ϫ4 Ϫ2 0 2
graph has the form:
y ؊ k ‫ ؍‬f(x ؊ h), where
Ϫ2
h ‫ 5؊ ؍‬and k ‫3؊ ؍‬
So, an equation of the image
graph is: y ؉ 3 ‫ ؍‬f(x ؉ 5)
b) y The graph of y ‫ ؍‬f(x) has a local
10 maximum at (2, 9).
This graph has a local maximum
8 at (5, 11).
So, the graph of y ‫ ؍‬f(x) was
6
translated 3 units right and
4 2 units up.
The equation of the image graph
2
y Ϫ 2 ϭ f(x Ϫ 3) has the form: y ؊ k ‫ ؍‬f(x ؊ h),
x where h ‫ 3 ؍‬and k ‫2 ؍‬
0 2 4 6 8 10 So, an equation of the image
graph is: y ؊ 2 ‫ ؍‬f(x ؊ 3)
28 Chapter 3: Transforming Graphs of Functions—Checkpoint—Solutions DO NOT COPY. ©P

4. 04_ch03a_pre-calculas12_wncp_solution.qxd 5/17/12 7:31 PM Page 29
Home Quit
3.2
4. Multiple Choice The graph of y = f(x) was y
reflected in the x-axis. Which graph below 4
y ϭ f(x)
is its reflection image?
2
x
0 2
A. y B. y
x
4
Ϫ2 0 2 4
Ϫ2
x
Ϫ2 0
C. y D. y
x
4
0 4
Ϫ2 2
x
Ϫ4
Ϫ4 Ϫ2
5. Here is the graph of y = k(x). On the same y
grid, sketch and label the graph of each 4
function below, then state its domain and
2
range. y ϭ k(Ϫx) y ϭ k(x)
x
a) y = -k(x) Ϫ4 0 4
y ϭ Ϫk(x)
The graph of y ‫؊ ؍‬k(x) is the image of the Ϫ2
graph of y ‫ ؍‬k(x) after a reflection in
Ϫ4
the x-axis.
Mark some lattice points on y ‫ ؍‬k(x),
then reflect them in the x-axis. Mark these image points, then join them.
Domain: x ç ‫ޒ‬
Range: y ◊ ؊2
b) y = k(-x)
The graph of y ‫ ؍‬k(؊x) is the image of the graph of y ‫ ؍‬k(x) after a
reflection in the y-axis.
Mark some lattice points on y ‫ ؍‬k(x), then reflect them in the y-axis.
Mark these image points, then join them.
Domain: x ç ‫ޒ‬
Range: y » 2
©P DO NOT COPY. Chapter 3: Transforming Graphs of Functions—Checkpoint—Solutions 29

5. 04_ch03a_pre-calculas12_wncp_solution.qxd 5/17/12 7:31 PM Page 30
Home Quit
6. The graph of y = -x3 + 3x2 - x + 3 was reflected in the y-axis 10
y
and its image is shown. What is an equation of the image? 8
6
When the graph of y ‫ ؍‬f(x) is reflected in the y-axis, the equation of its 4
image is y ‫ ؍‬f(؊x). 2
x
So, an equation of the image is: Ϫ2 0 2
y ‫ ؍‬f(؊x)
y ‫؊(؊ ؍‬x)3 ؉ 3(؊x)2 ؊ (؊x) ؉ 3
y ‫ ؍‬x3 ؉ 3x 2 ؉ x ؉ 3
3.3
7. Multiple Choice The point (Ϫ6, 2) lies on the graph of y = f(x).
After vertical and horizontal stretches or compressions of the graph,
the equation of the image is y = 3f(2x). Which point is the image of
(Ϫ6, 2)?
A. (Ϫ3, 6) B. (Ϫ12, 6) C. (Ϫ2, 4) D. (Ϫ18, 1)
8. Here is the graph of y = h(x). y
12
y ϭ 2h(4x)
On the same grid, sketch the
8 y ϭ h(x)
graph of each function below,
then state its domain and range. 4 1
yϭ h(Ϫ2x)
1 3
a) y = 3h(-2x) x
Ϫ4 2 4 6 8
Compare y ‫ ؍‬ah(bx) to Ϫ4
1 1
y ‫ ؍‬h( ؊2x): a ‫؍‬ and b ‫2؊ ؍‬
3 3
So, the graph of y ‫ ؍‬h(x) is vertically compressed by a factor
1 1
of , horizontally compressed by a factor of , then reflected
3 2
in the y-axis. Use mental math and the transformation: (x, y)
on y ‫ ؍‬h(x) corresponds to a , yb on y ‫ ؍‬h(؊2x), to
x 1 1
؊2 3 3
mark some image points, then join them.
Domain: ؊4 ◊ x ◊ 2; range: ؊1 ◊ y ◊ 2
b) y = 2h(4x)
Compare y ‫ ؍‬ah(bx) to y ‫2 ؍‬h(4x): a ‫ 2 ؍‬and b ‫4 ؍‬
So, the graph of y ‫ ؍‬h(x) is vertically stretched by a factor of 2, and
1
horizontally compressed by a factor of . Use mental math and the
4
transformation: (x, y) on y ‫ ؍‬h(x) corresponds to a , 2yb on y ‫2 ؍‬h(4x),
x
4
to mark some image points, then join them.
Domain: ؊1 ◊ x ◊ 2; range: ؊6 ◊ y ◊ 12
30 Chapter 3: Transforming Graphs of Functions—Checkpoint—Solutions DO NOT COPY. ©P

6. 04_ch03a_pre-calculas12_wncp_solution.qxd 5/17/12 7:31 PM Page 31
Home Quit
9. The graph of y = g(x) is the image of 4
y y ϭ f(x)
B
A
the graph of y = f(x) after a vertical
x
and/or horizontal stretch and/or 0 4 8 12 16
reflection. Corresponding points are Ϫ4
AЈ
labelled. Write an equation of the image
Ϫ8 y ϭ g(x)
graph in terms of the function f. BЈ
Point A(4, 2) on y ‫ ؍‬f(x) corresponds to point A؅(8, ؊6) on y ‫ ؍‬g(x).
An equation for the image graph after a vertical or horizontal stretch or
compression can be written in the form y ‫ ؍‬af(bx).
A point (x, y) on y ‫ ؍‬f(x) corresponds to the point a , ayb on y ‫ ؍‬af(bx).
x
b
The image of A(4, 2) is a , a(2)b , which is A؅(8, ؊6).
4
b
1
Equate the x-coordinates: b ‫؍‬
2
Equate the y-coordinates: a ‫3؊ ؍‬
So, an equation of y ‫ ؍‬g(x) is: y ‫3؊ ؍‬f a xb
1
2
I used the coordinates of B and B؅, and mental math to verify the equation.
©P DO NOT COPY. Chapter 3: Transforming Graphs of Functions—Checkpoint—Solutions 31