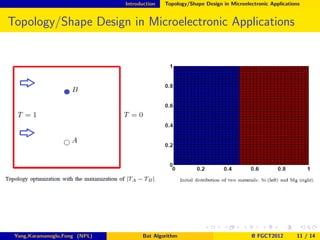
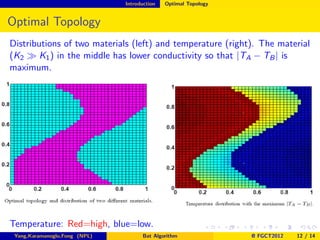
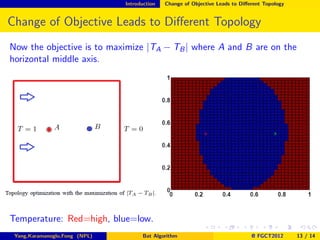
The document discusses the bat algorithm, developed by Xin-She Yang in 2010, for topology optimization in microelectronic applications, focusing on material distribution to optimize heat transfer. It outlines the algorithm's advantages, variants, applications, and presents an example of its use in optimizing a speed reducer design. The document also explores how changing objectives can affect the optimal topology in heat transfer scenarios.

1. Bat Algorithm for Topology Optimization
in Microelectronic Applications
Xin-She Yang, Mehmet Karamanoglu and Simon Fong
@ FGCT2012
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 1 / 14

2. Introduction Topology/Shape Design
Topology/Shape Design
Given a geometry (say, a rectangle), how to distribute two different
materials, with thermal conductivities K1 and K2 , respectively, so as to
meet a specific design problem for heat transfer applications?
To maximize |TA − TB |?
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 2 / 14

3. Introduction Should we use different methods for different problems?
Should we use different methods for different problems?
Changing the landscape:
Space mapping, surrogate, trust-region, dimension reduction ...
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 3 / 14

4. Introduction Bat Algorithm, Developed by Xin-She Yang (in 2010)
Bat Algorithm, Developed by Xin-She Yang (in 2010)
BBC Video
Microbats use echolocation for hunting
Ultrasonic short pulses as loud as 110dB with a short period of 5 to
20 ms. Frequencies of 25 kHz to 100 kHz.
Speed up the pulse-emission rate, and increase loudness, when
homing at a prey.
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 4 / 14

5. Introduction Bat Algorithm (Yang 2010)
Bat Algorithm (Yang 2010)
Acoustics of bat echolocation
v
λ = ∼ 2 mm to 14 mm.
f
Rules used in the bat algorithm:
fi = fmin + (fmax − fmin )β, β ∈ [0, 1],
vt+1 = vit + (xt − x∗ )fi ,
i i xt+1 = xt + vt .
i i i
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 5 / 14

6. Introduction Bat Algorithm (Yang 2010)
Bat Algorithm (Yang 2010)
Acoustics of bat echolocation
v
λ = ∼ 2 mm to 14 mm.
f
Rules used in the bat algorithm:
fi = fmin + (fmax − fmin )β, β ∈ [0, 1],
vt+1 = vit + (xt − x∗ )fi ,
i i xt+1 = xt + vt .
i i i
Variations of Loudness and Pulse Rate
At+1 ← αAt ,
i i α ∈ (0, 1],
rit+1 = ri0 [1 − exp(−γt)].
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 5 / 14

7. Introduction Advantages
Advantages
Dynamic exploration and exploitation
Simple to implement, and it searches for optimality using frequency
tuning.
Initially, BA focuses on more explorative moves, and then switch to
more exploitation when optimality is approaching.
Balance between exploration and exploitation is not static, it is
dynamic!
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 6 / 14

8. Introduction Variants and Applications
Variants and Applications
Continuous optimization
Binary bat algorithm for image processing and classifications
Spam filtering
Training neural networks
Multobjective bat algorithm
Clustering ...
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 7 / 14

9. Introduction Speed Reducer/Gear Box Design
Speed Reducer/Gear Box Design
Mixed-Integer Programming:
Continuous variables and integers.
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 8 / 14

10. Introduction
2 2
f (x1 , x2 , x3 , x4 , x5 , x6 , x7 ) = 0.7854x1 x2 (3.3333x3 + 14.9334x3 − 43.0934)
2 2 3 3 2 2
−1.508x1 (x6 + x7 ) + 7.4777(x6 + x7 ) + 0.7854(x4 x6 + x5 x7 ),
subject to
27 397.5
g1 = 2
x1 x2 x3
− 1 ≤ 0, g2 = 2 2
x1 x2 x3
− 1 ≤ 0,
1.93x 3 1.93x5 3
g3 = x x d44 − 1 ≤ 0, g4 = 4
x2 x3 d2
− 1 ≤ 0,
2 3 1
g5 = 110x 3 ( 745x4 )2 + 16.9 × 106 − 1 ≤ 0,
1
hx3
6
1 745x5 2
g6 = 85x 3 ( hx3 ) + 157.5 × 106 − 1 ≤ 0,
7
g7 = x403 − 1 ≤ 0,
2x
g8 = 5x12 − 1 ≤ 0,
x
x1
g9 = 12x2 − 1 ≤ 0, g10 = 1.5xx4
6 +1.9
− 1 ≤ 0,
g11 = 1.1xx57 +1.9
− 1 ≤ 0.
Simple bounds are 2.6 ≤ x1 ≤ 3.6, 0.7 ≤ h ≤ 0.8, 17 ≤ x3 ≤ 28,
7.3 ≤ x4 ≤ 8.3, 7.8 ≤ x5 ≤ 8.3, 2.9 ≤ x6 ≤ 3.9, and 5.0 ≤ x7 ≤ 5.5. z
must be integers.
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 9 / 14

11. Introduction
The best solution obtained by BA is
fmin = 2993.7495888,
with
x∗ = (3.5, 0.7, 17, 7.3, 7.8, 3.34446445, 5.285350625),
which is better than the solution in the literature (Cagnina et al., 2008)
f∗ = 2996.348165.
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 10 / 14

12. Introduction Topology/Shape Design in Microelectronic Applications
Topology/Shape Design in Microelectronic Applications
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 11 / 14

13. Introduction Optimal Topology
Optimal Topology
Distributions of two materials (left) and temperature (right). The material
(K2 K1 ) in the middle has lower conductivity so that |TA − TB | is
maximum.
Temperature: Red=high, blue=low.
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 12 / 14

14. Introduction Change of Objective Leads to Different Topology
Change of Objective Leads to Different Topology
Now the objective is to maximize |TA − TB | where A and B are on the
horizontal middle axis.
Temperature: Red=high, blue=low.
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 13 / 14

15. Introduction Bibliography
Bibliography
A. Evgrafov, K. Maute, R. G. Yang and M. L. Dunn, Topology optimization
for nano-scale heat transfer, Int. J. Num. Methods in Engrg., 77 (2),
285-300 (2009).
X. S. Yang, A New Metaheuristic Bat-Inspired Algorithm, in: Nature
Inspired Cooperative Strategies for Optimization (NISCO 2010) (Eds. J. R.
Gonzalez et al.), Studies in Computational Intelligence, Springer Berlin, 284,
Springer, 65-74 (2010).
X. S. Yang, bat algorithm for multi-objective optimisation, Int. J.
Bio-Inspired Computation, Vol. 3, 267-274 (2011).
X. S. Yang, Engineering Optimization: An Introduction With Metaheuristic
Applications, John Wiley and Sons, USA, (2010).
V. V. Zhirnov, R. K. Cavin, J. A. Hutchby, G. I. Bourianoff, Limits to binary
logic switch scaling - a gedanken model, Proc. of the IEEE, 91(11),
1934-1939 (2003).
Thank you very much :)
Yang,Karamanoglu,Fong (NPL) Bat Algorithm @ FGCT2012 14 / 14