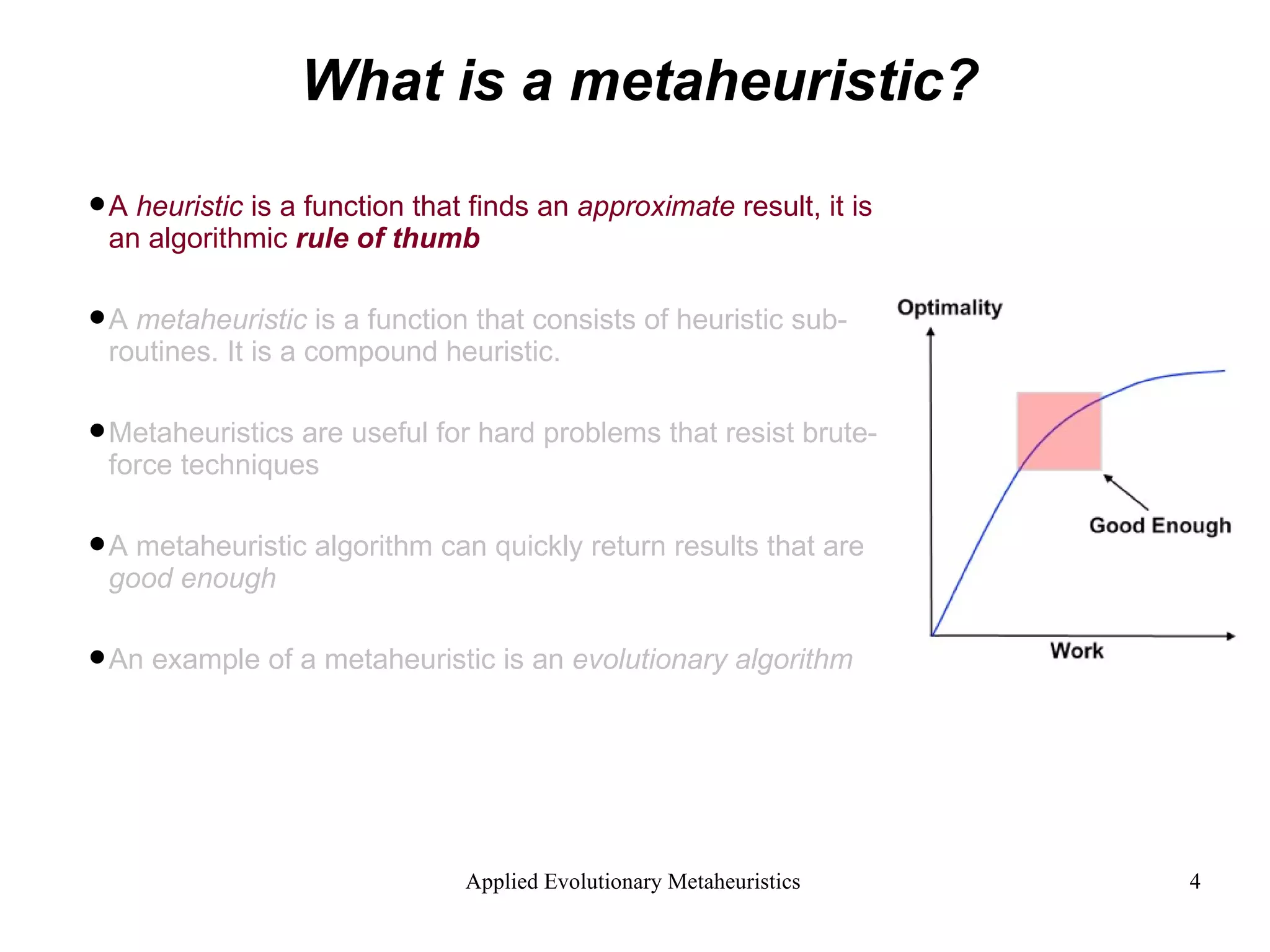
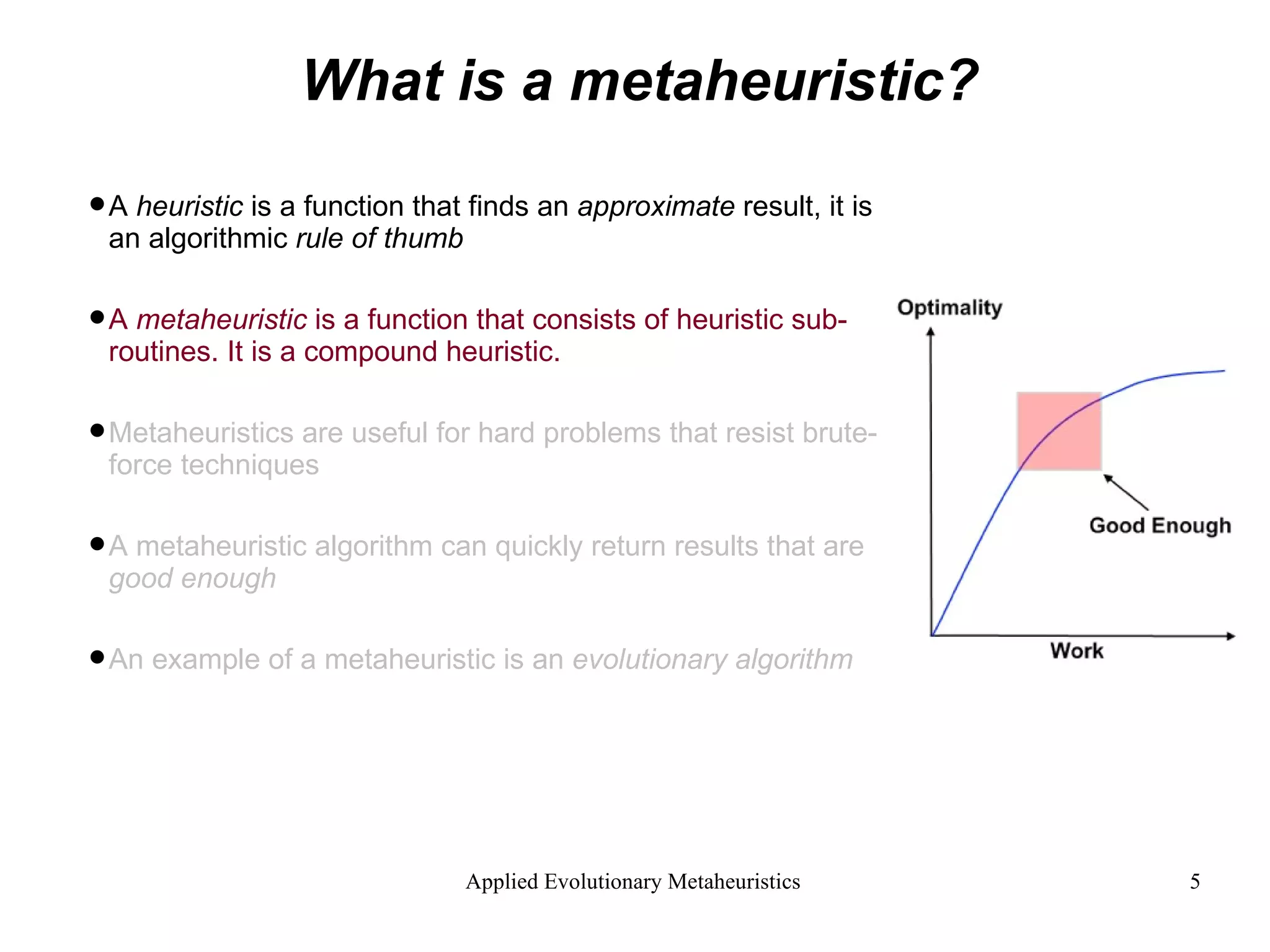
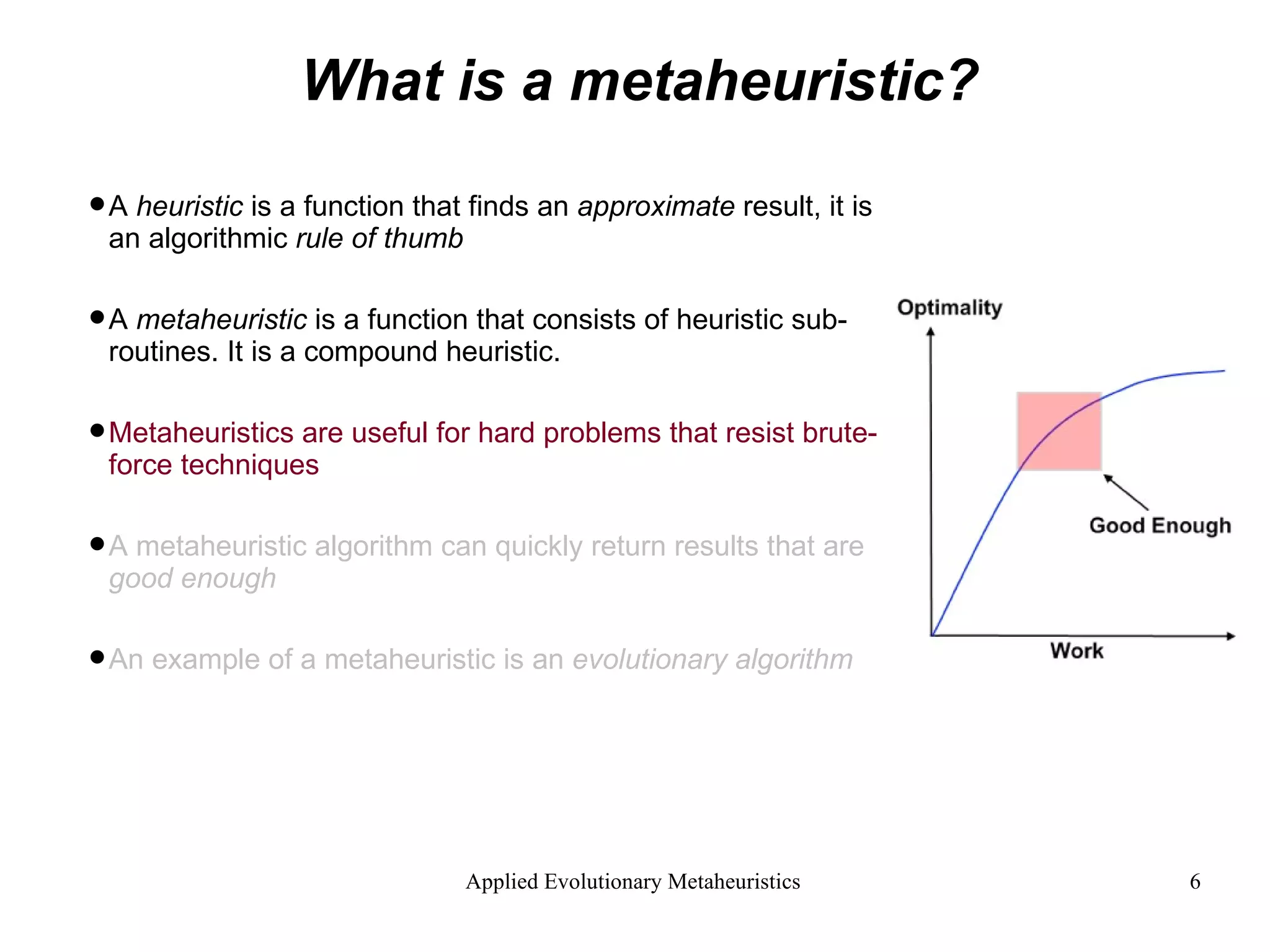
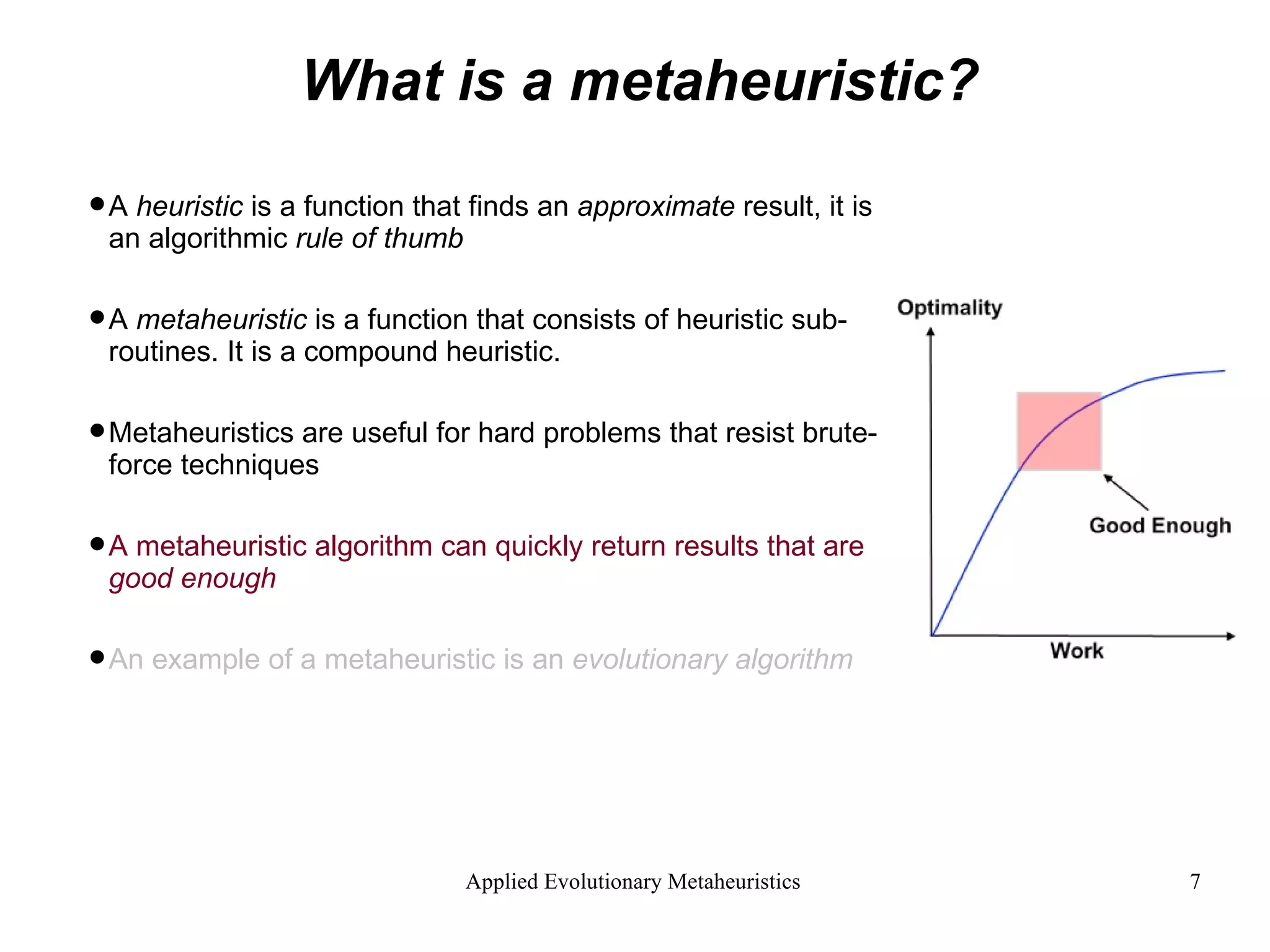
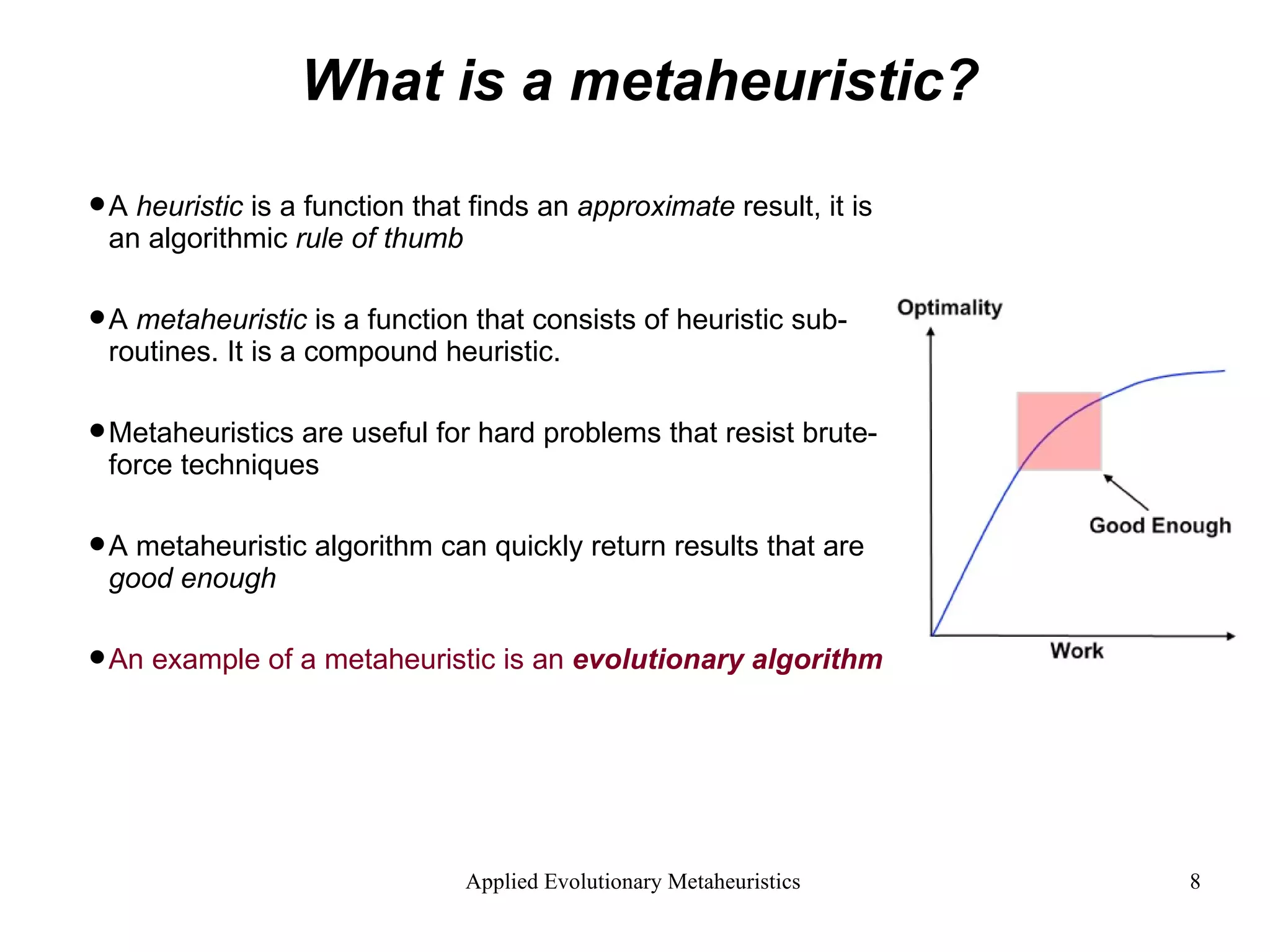
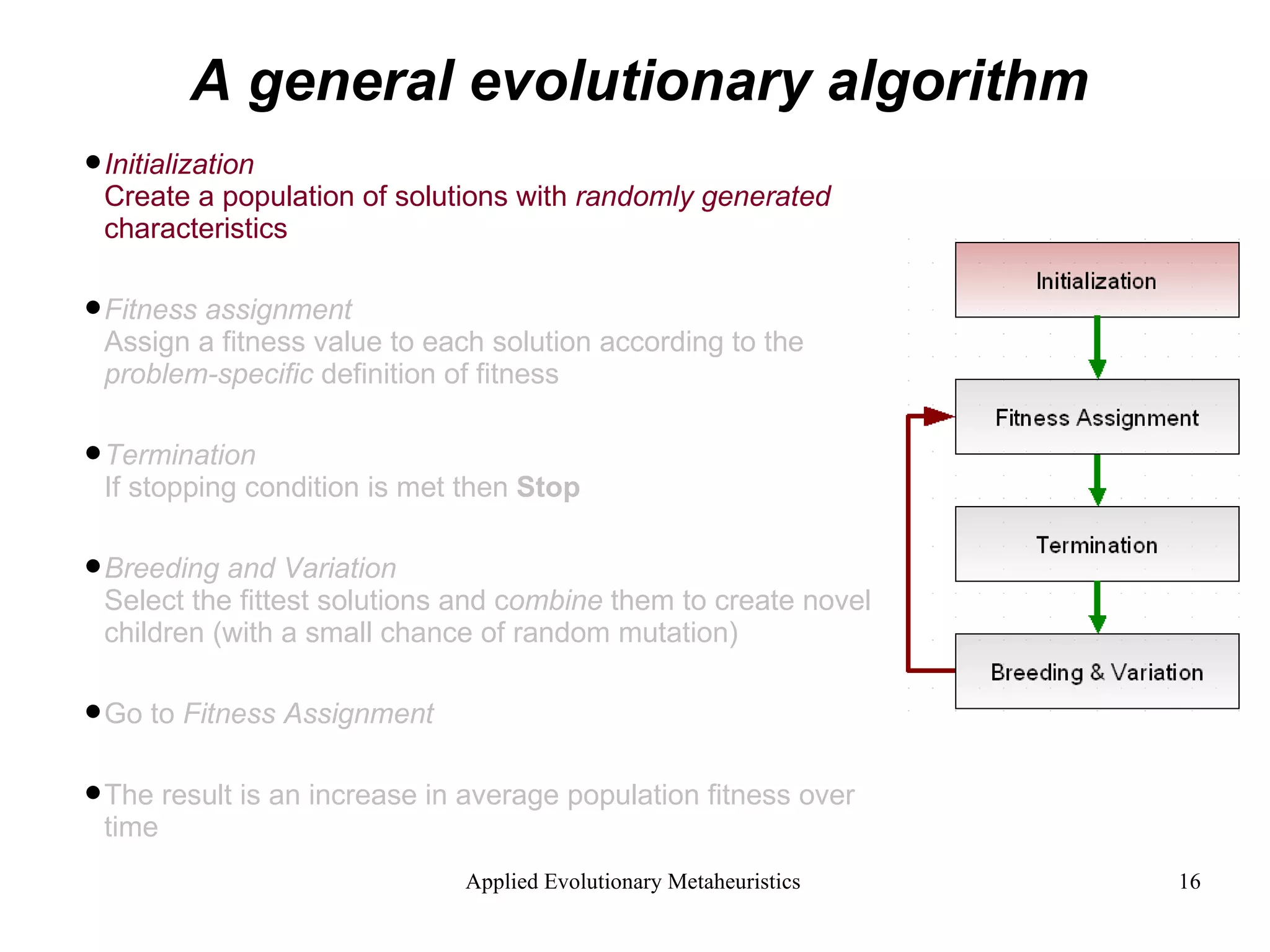
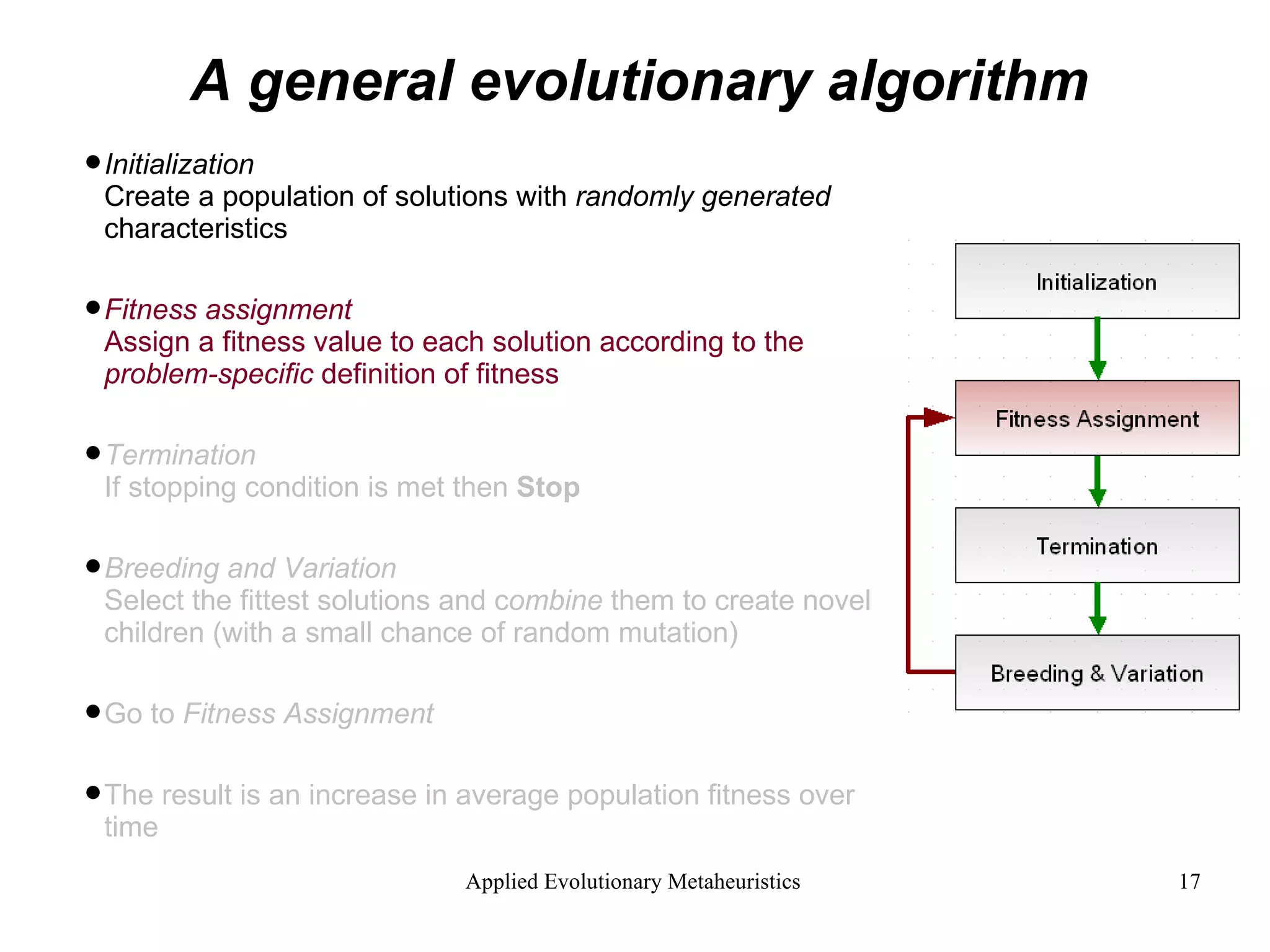
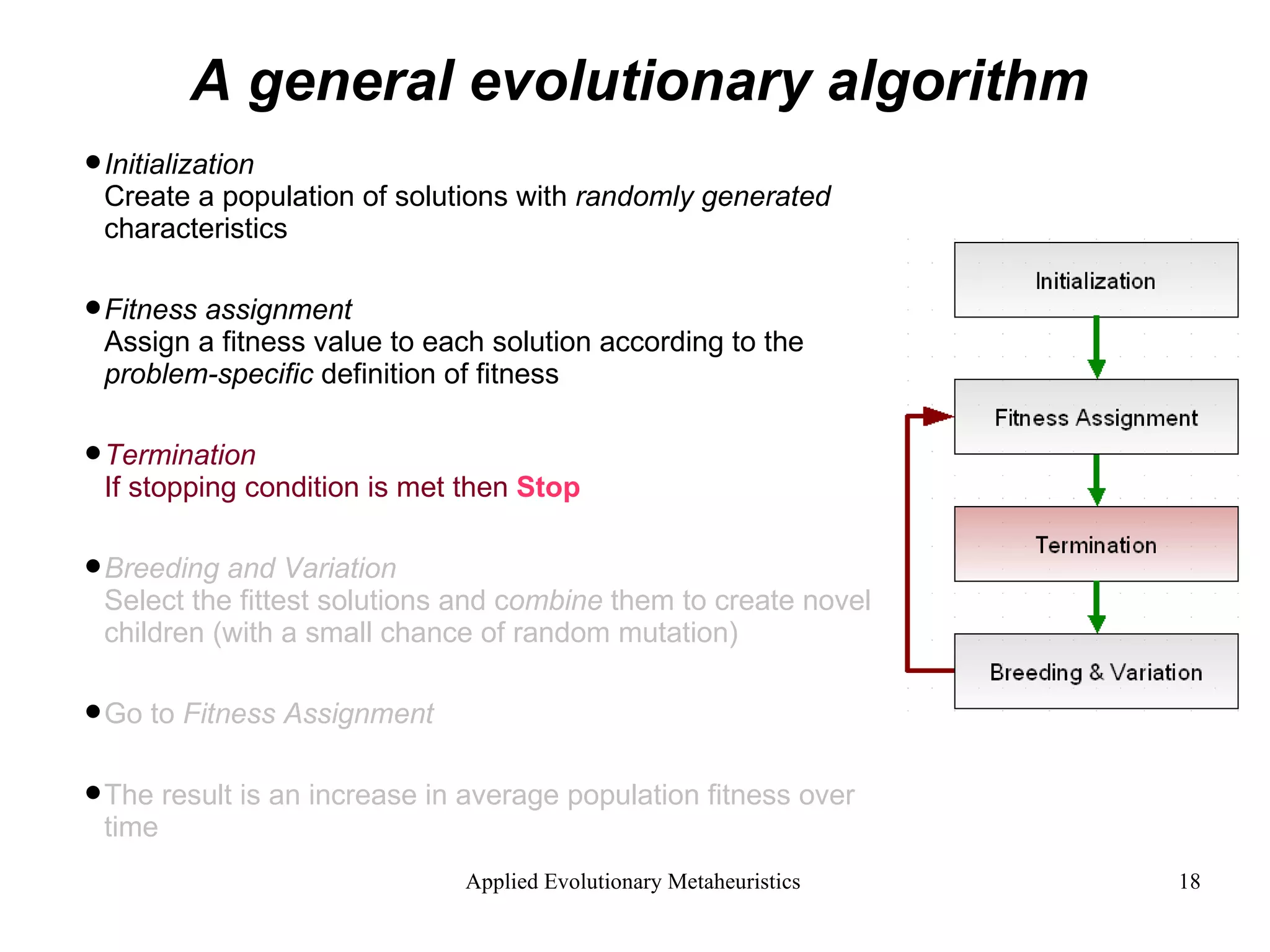
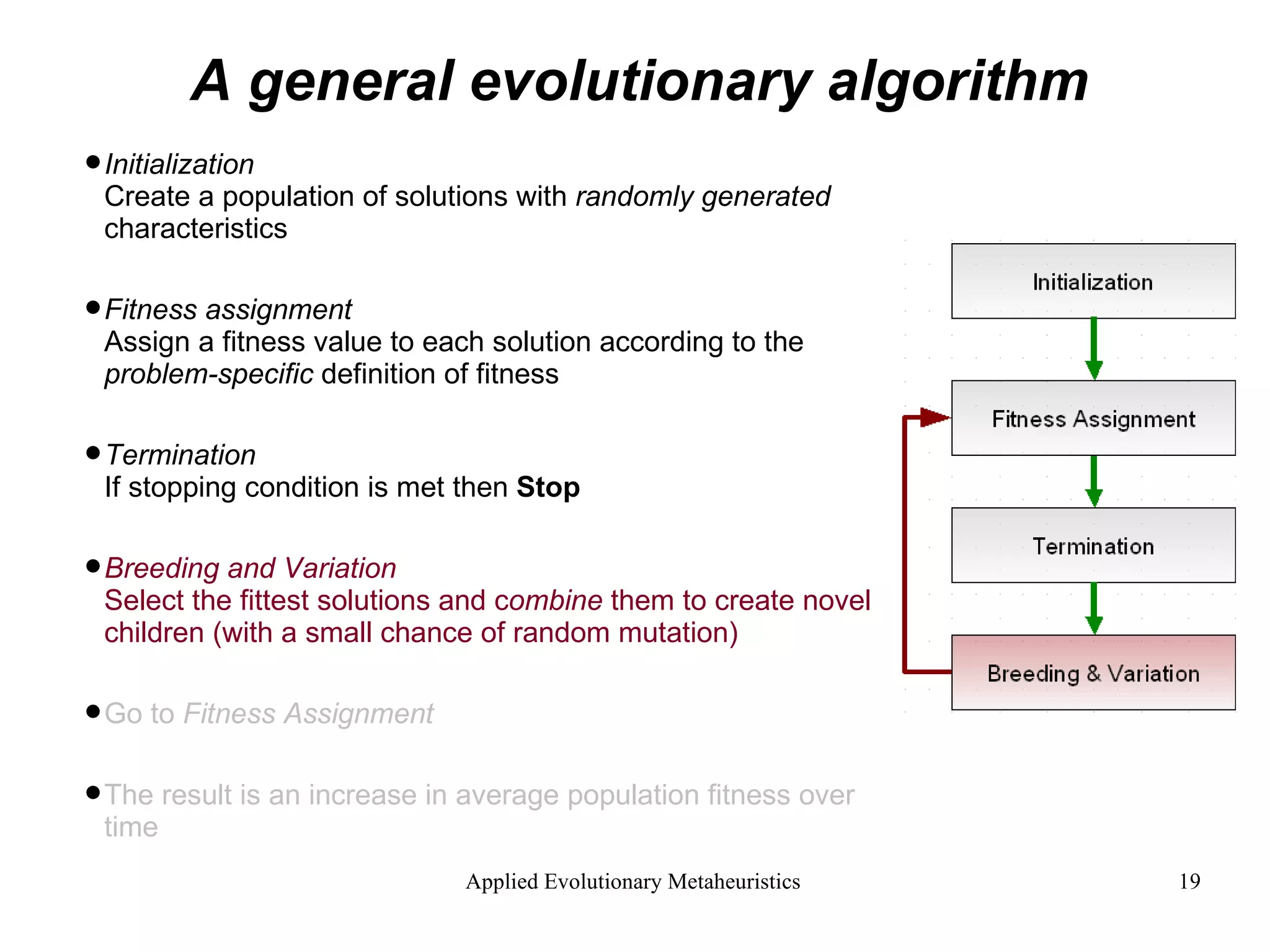
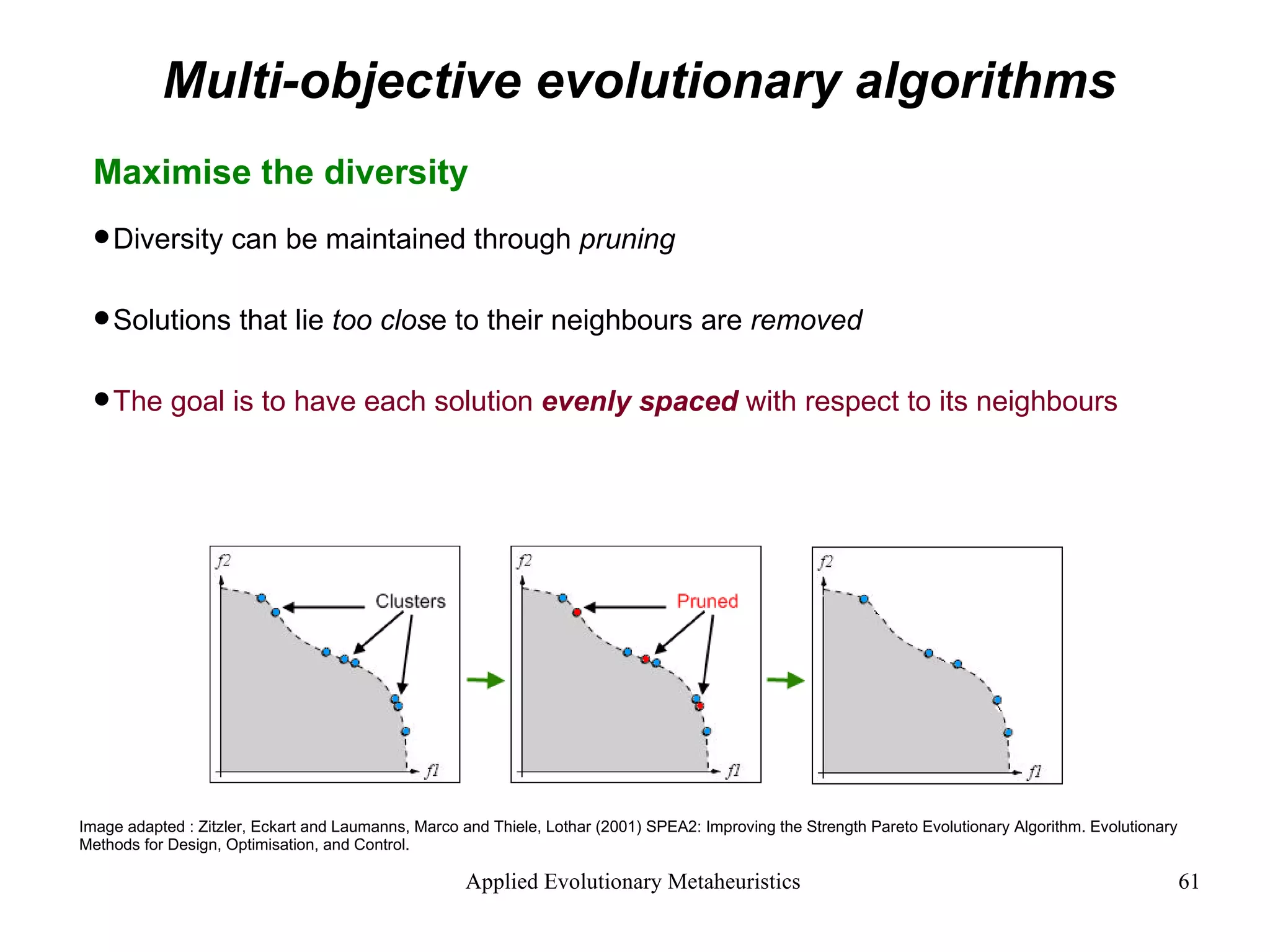
The document introduces applied evolutionary metaheuristics, defining metaheuristics as compound heuristics useful for solving complex problems through algorithms. It describes evolutionary algorithms that mimic natural selection to find solutions, highlighting their ability to handle large state-spaces via implicit parallelism. Additionally, it differentiates between single-objective and multi-objective evolutionary algorithms, demonstrating their application in problems like the traveling salesperson problem and the concept of Pareto optimality in multi-objective scenarios.

















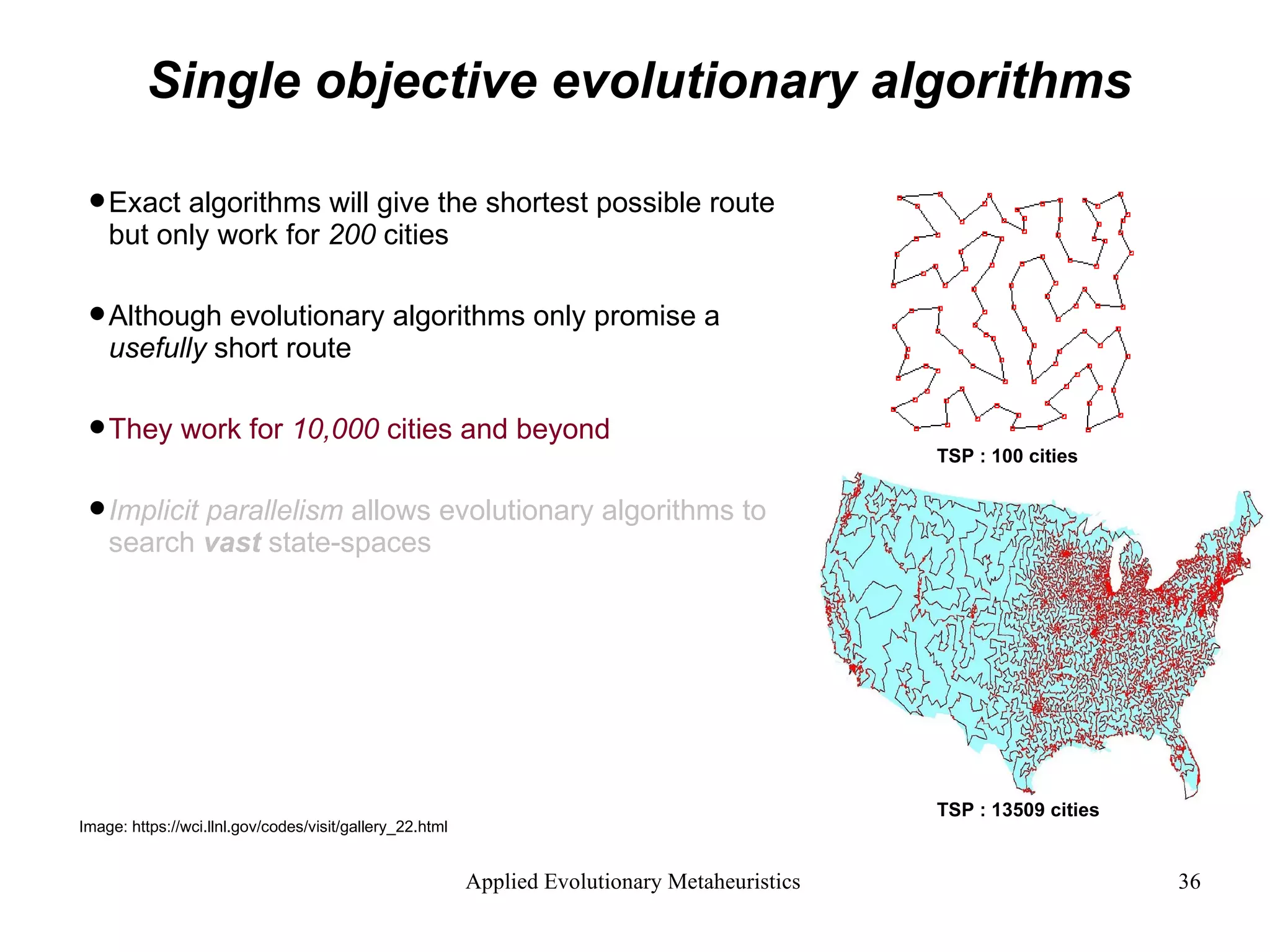
![Single objective evolutionary algorithms A single objective evolutionary algorithm exists to solve single objective problems A standard single objective problem is the Travelling Salesperson Problem or TSP. This states: Given a number of cities and the distance from any city to any other city. What is the shortest round-trip route that visits each city exactly once and then returns to the starting city? Objective = [minimise route length] Image: http://www.cs.princeton.edu/courses/archive/spr05/cos126/assignments/tsp.html TSP : 1000 Cities](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-29-2048.jpg)
![Single objective evolutionary algorithms A single objective evolutionary algorithm exists to solve single objective problems A standard single objective problem is the Travelling Salesperson Problem or TSP. This states: Given a number of cities and the distance from any city to any other city. What is the shortest round-trip route that visits each city exactly once and then returns to the starting city? Objective = [minimise route length] Image: http://www.cs.princeton.edu/courses/archive/spr05/cos126/assignments/tsp.html TSP : 1000 Cities](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-30-2048.jpg)
![Single objective evolutionary algorithms A single objective evolutionary algorithm exists to solve single objective problems A standard single objective problem is the Travelling Salesperson Problem or TSP. This states: Given a number of cities and the distance from any city to any other city. What is the shortest round-trip route that visits each city exactly once and then returns to the starting city? Objective = [minimise route length] Image: http://www.cs.princeton.edu/courses/archive/spr05/cos126/assignments/tsp.html TSP : 1000 Cities](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-31-2048.jpg)
![Single objective evolutionary algorithms A single objective evolutionary algorithm exists to solve single objective problems A standard single objective problem is the Travelling Salesperson Problem or TSP. This states: Given a number of cities and the distance from any city to any other city. What is the shortest round-trip route that visits each city exactly once and then returns to the starting city? Objective = [minimise route length] Image: http://www.cs.princeton.edu/courses/archive/spr05/cos126/assignments/tsp.html TSP : 1000 Cities](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-32-2048.jpg)
![Single objective evolutionary algorithms A single objective evolutionary algorithm exists to solve single objective problems A standard single objective problem is the Travelling Salesperson Problem or TSP. This states: Given a number of cities and the distance from any city to any other city. What is the shortest round-trip route that visits each city exactly once and then returns to the starting city? Objective = [ minimise route length ] Image: http://www.cs.princeton.edu/courses/archive/spr05/cos126/assignments/tsp.html TSP : 1000 Cities](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-33-2048.jpg)








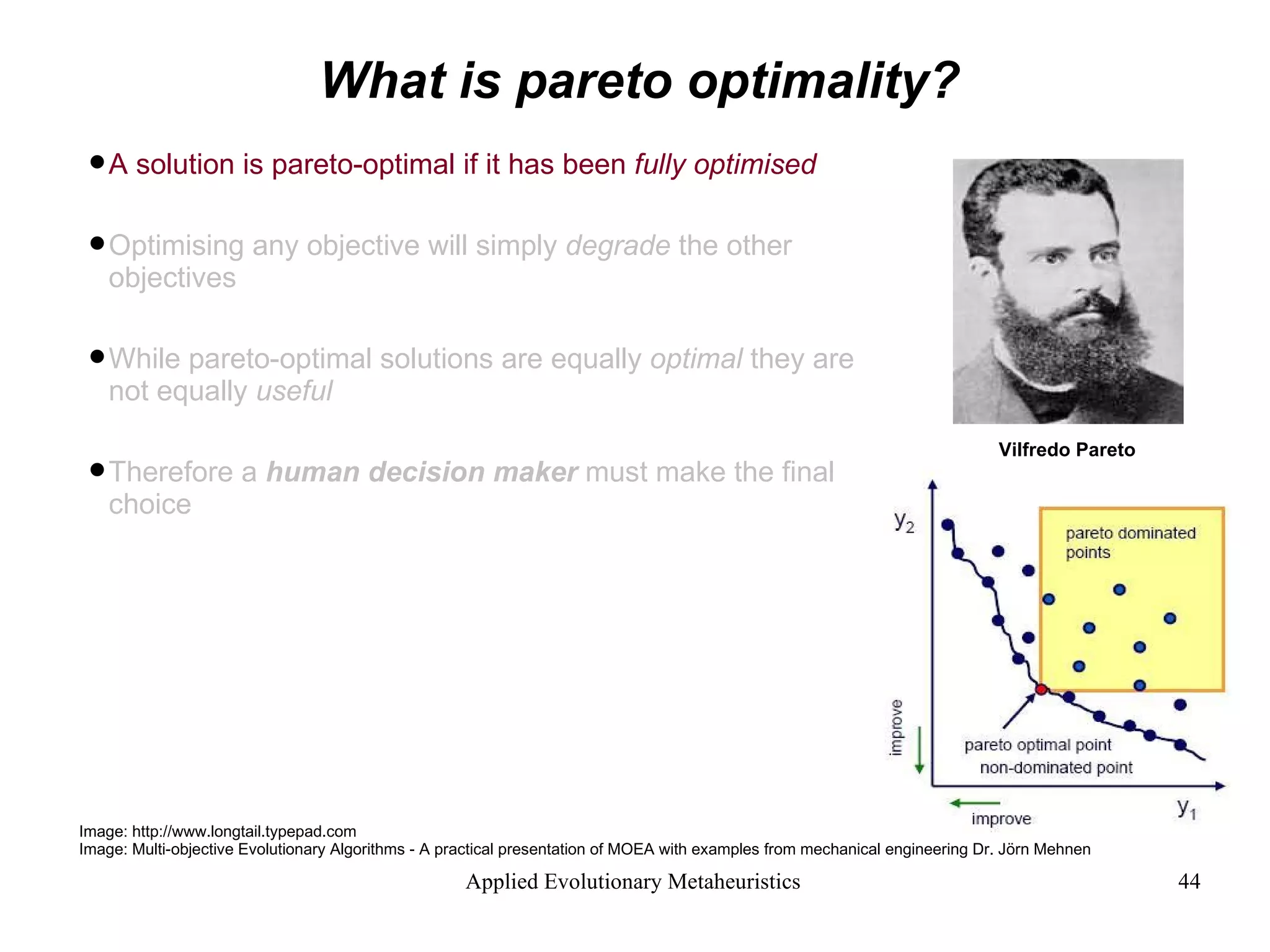
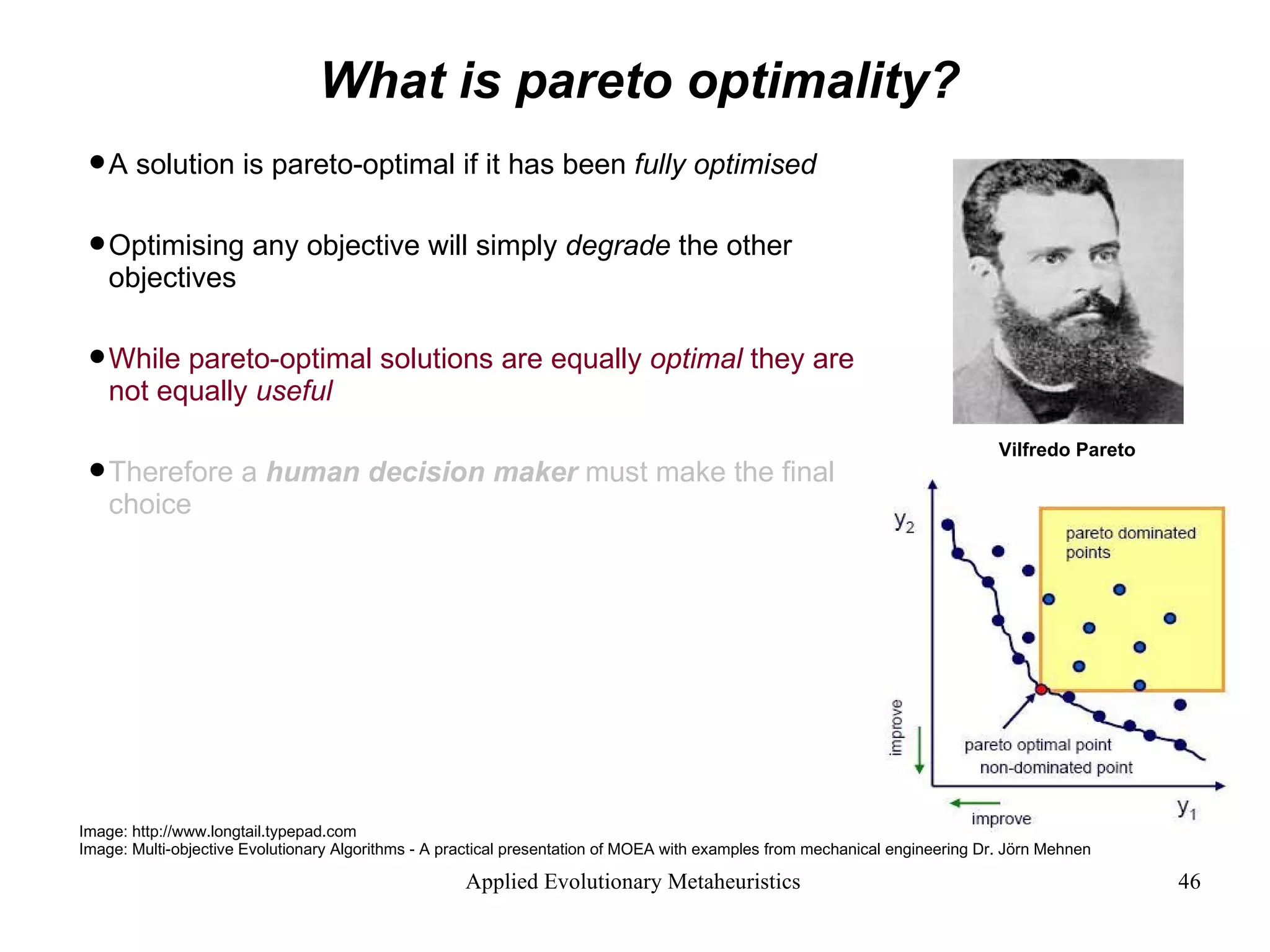
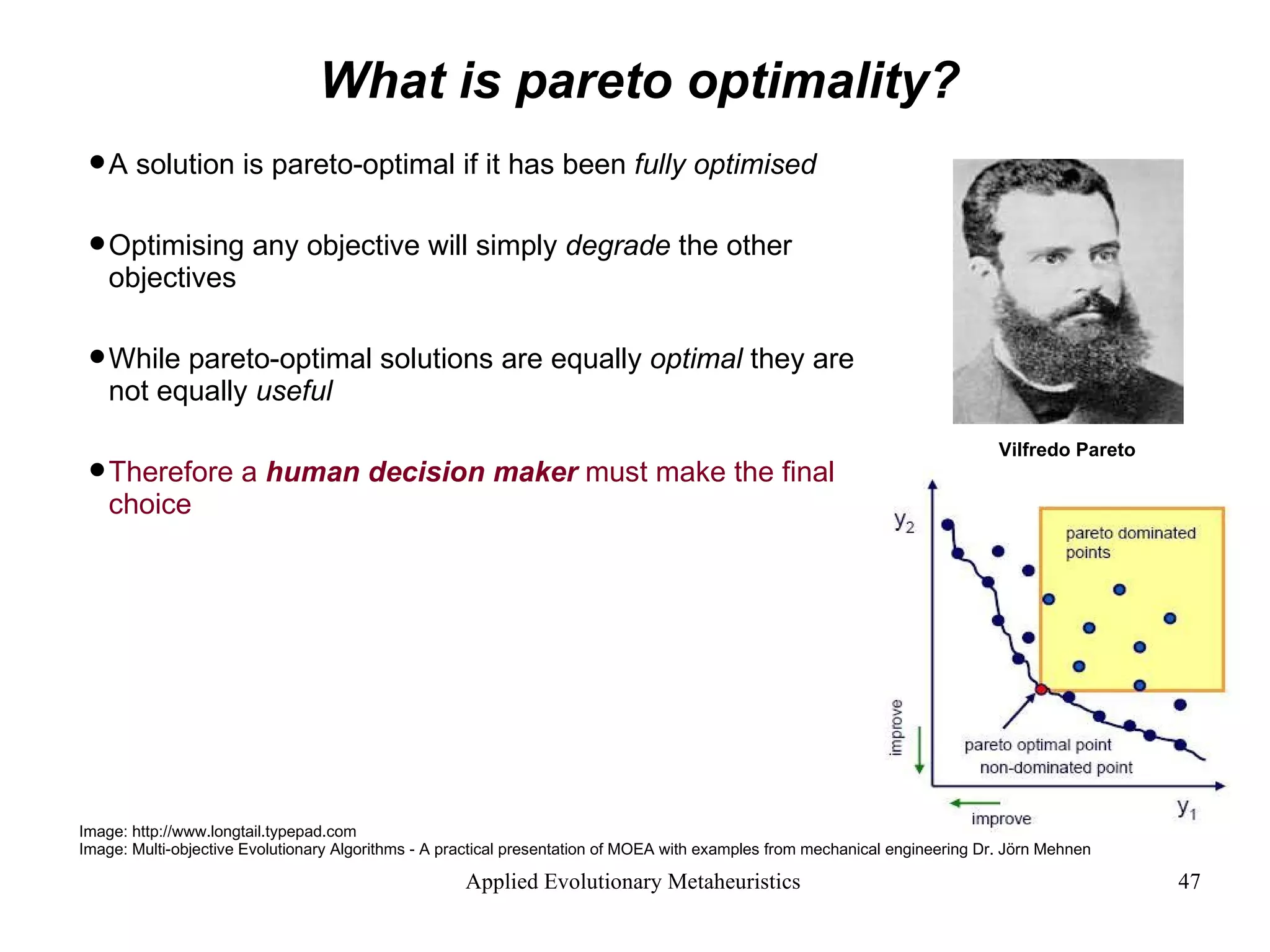
![What is pareto optimality? [pa-rih-toe]](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-43-2048.jpg)

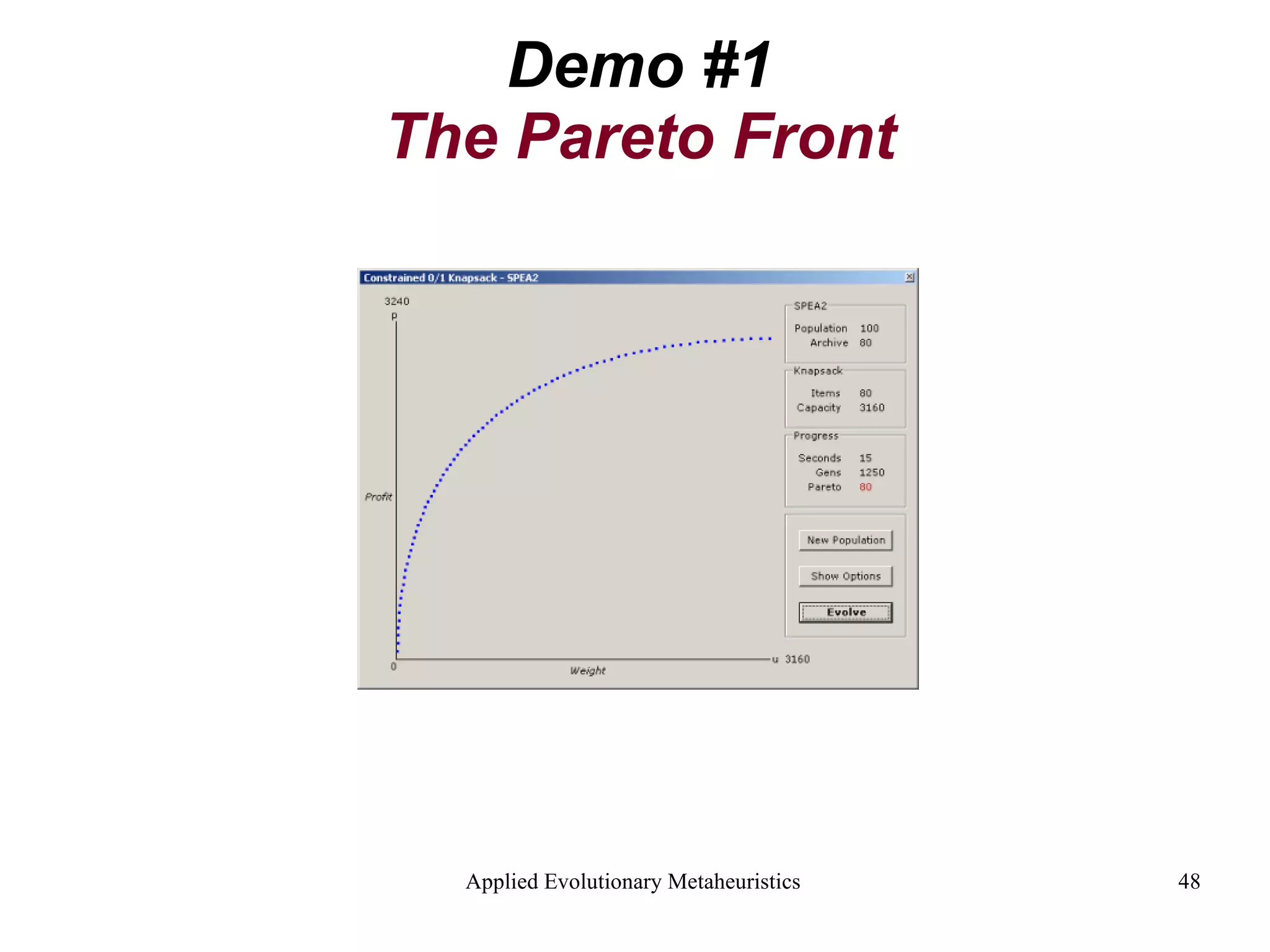














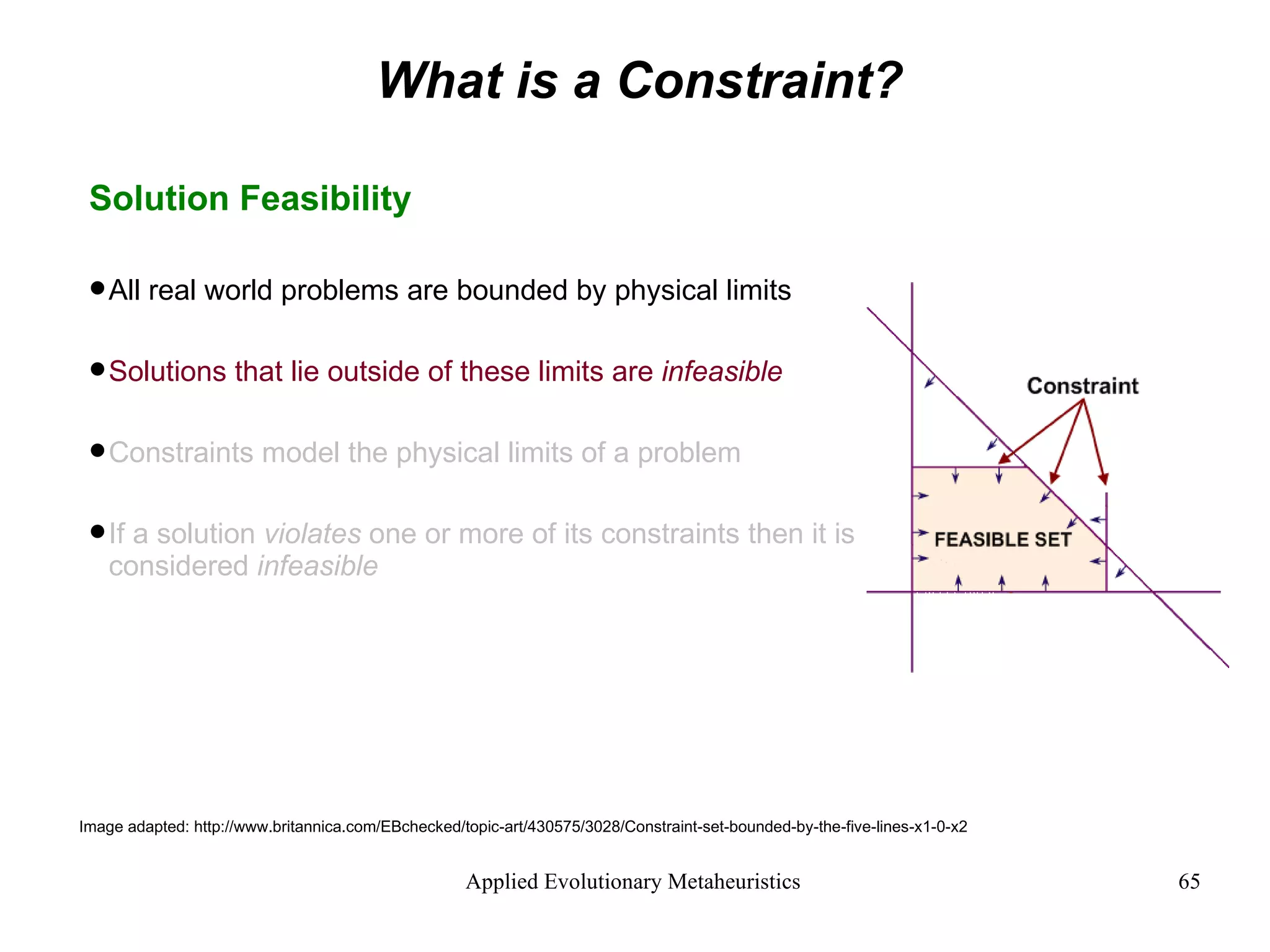
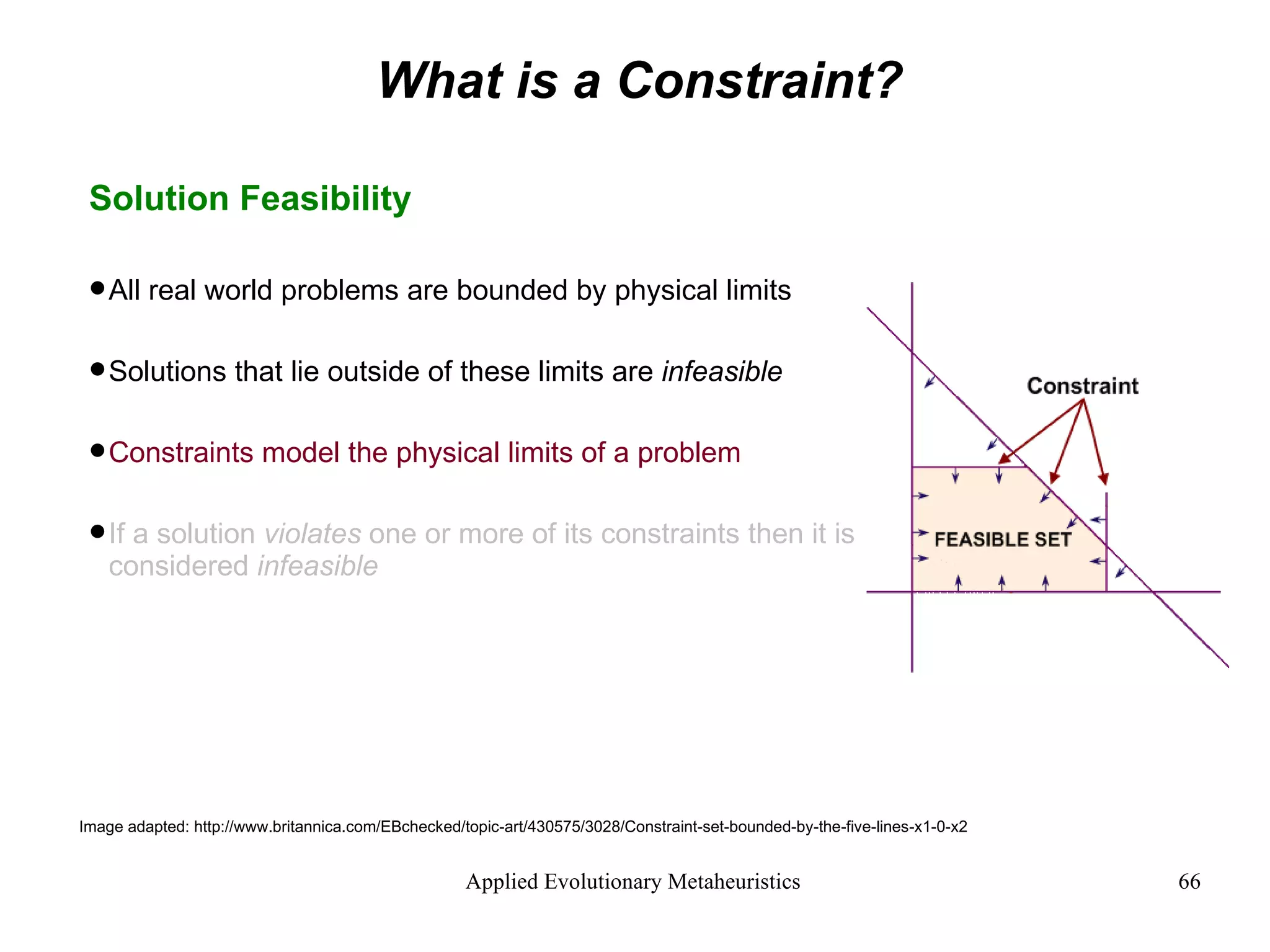
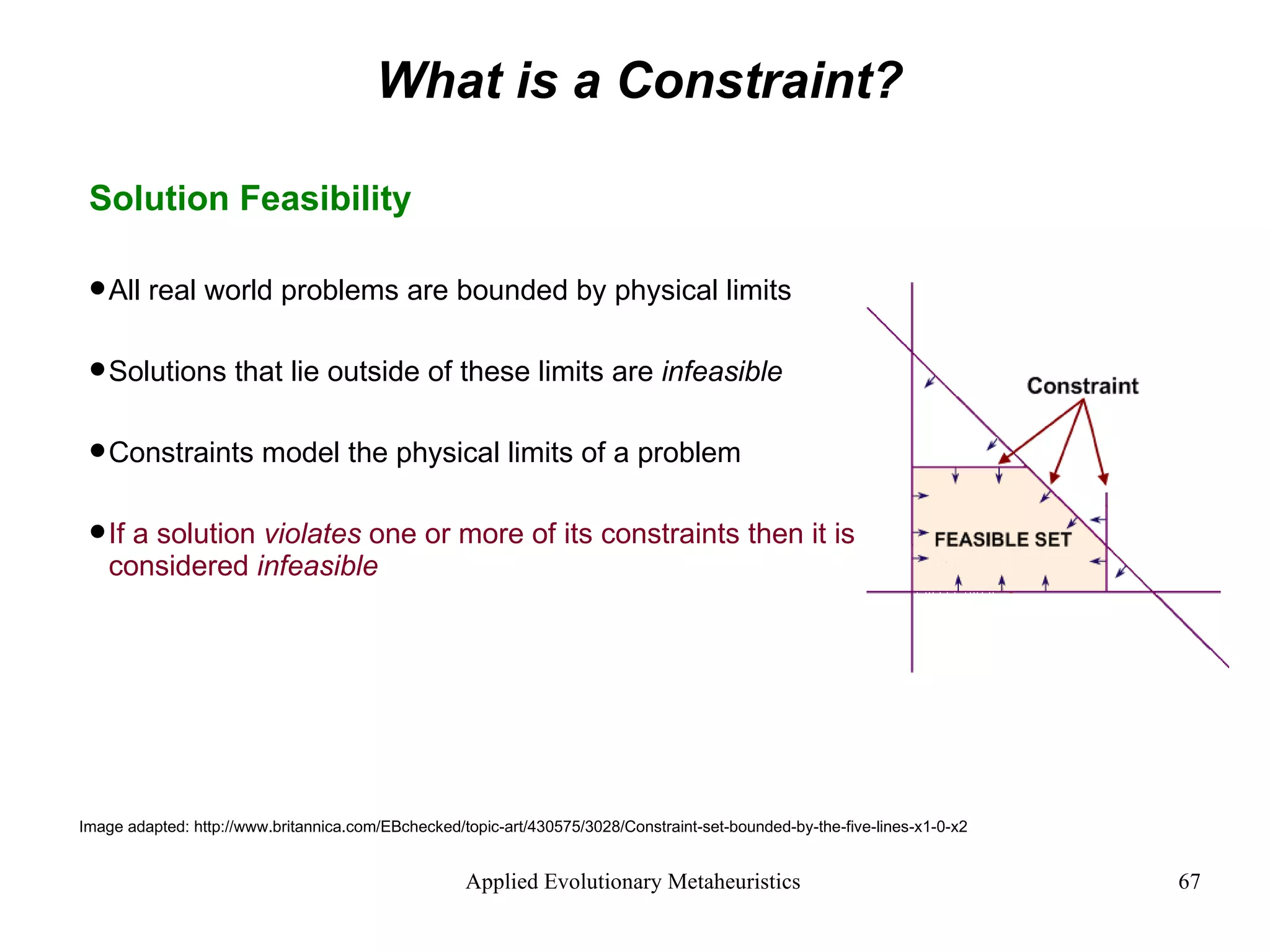
![What is a Constraint? The Problem with Constraints It is hard to randomly search for an initial population of feasible solutions Better to generate an infeasible population and evolve it towards feasibility This is done by adding a new infeasibility objective to the multi-objective problem: Infeasibility Objective = [minimise population infeasibility] Image: http://en.wikipedia.org/wiki/Image:Random_walk_in2D_closeup.png Image: http://www.outbacksoftware.com/mathematica/mathematica-intro.html Random walk - 3D Random walk - 2D](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-68-2048.jpg)
![What is a Constraint? The Problem with Constraints It is hard to randomly search for an initial population of feasible solutions Better to generate an infeasible population and evolve it towards feasibility This is done by adding a new infeasibility objective to the multi-objective problem: Infeasibility Objective = [minimise population infeasibility] Image: http://en.wikipedia.org/wiki/Image:Random_walk_in2D_closeup.png Image: http://www.outbacksoftware.com/mathematica/mathematica-intro.html Random walk - 3D Random walk - 2D](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-69-2048.jpg)
![What is a Constraint? The Problem with Constraints It is hard to randomly search for an initial population of feasible solutions Better to generate an infeasible population and evolve it towards feasibility This is done by adding a new infeasibility objective to the multi-objective problem: Infeasibility Objective = [ minimise population infeasibility ] Image: http://en.wikipedia.org/wiki/Image:Random_walk_in2D_closeup.png Image: http://www.outbacksoftware.com/mathematica/mathematica-intro.html Random walk - 3D Random walk - 2D](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-70-2048.jpg)














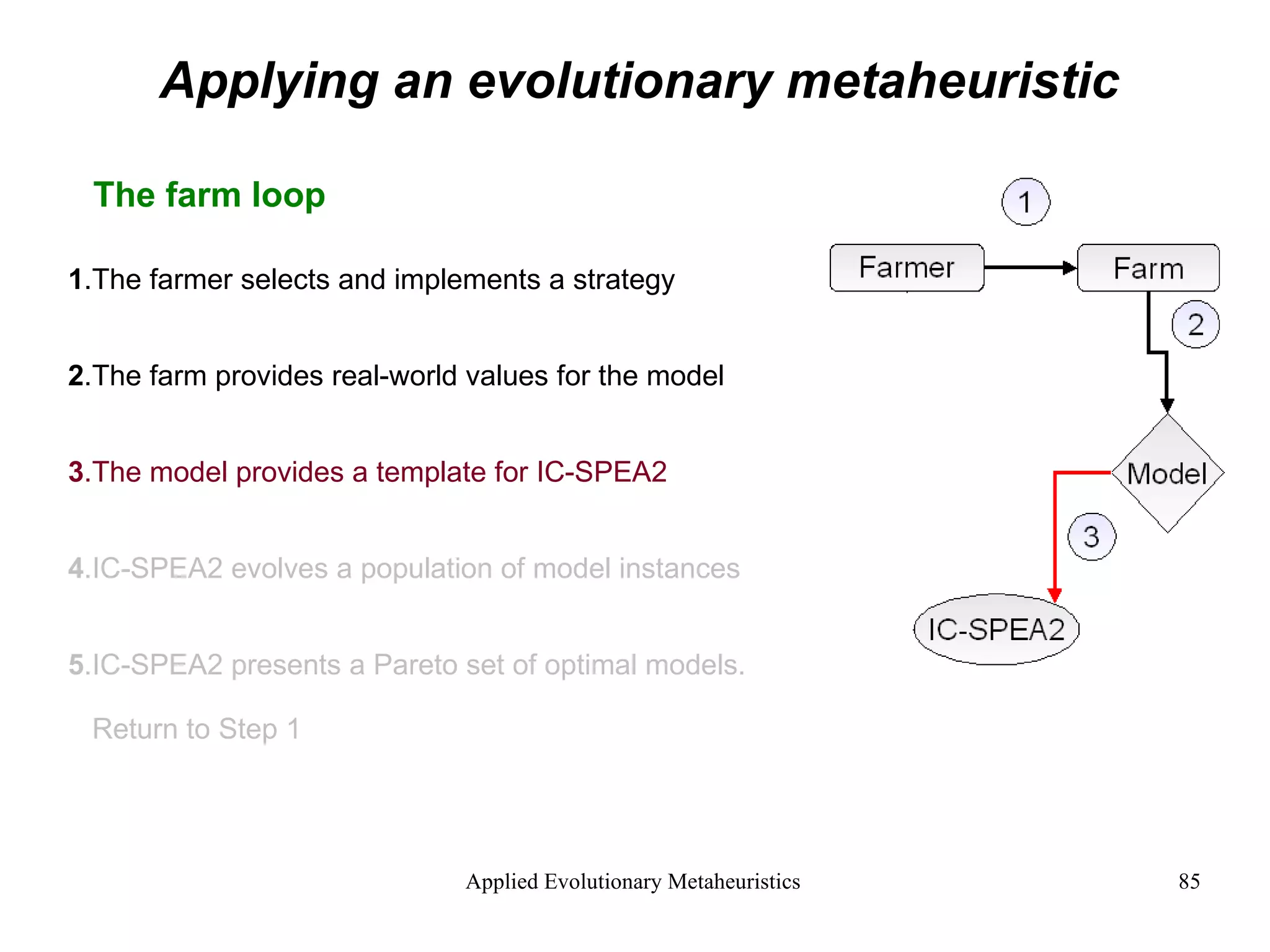











![Applying an evolutionary metaheuristic Discovering counter intuitive solutions As expected IC-SPEA2 returned multiple, pareto-optimal strategies Two solutions were of particular interest 1. The feeding strategy that maximised net revenue. 2. The feeding strategy that maximised live weight gain . Intuition suggests that heavy animals should sell for more money [maximum live weight gain] = [maximum net revenue] Yet IC-SPEA2 found a way to maximise net revenue while delivering lighter animals This counter-intuitive result has potential implications for farm sustainability](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-97-2048.jpg)
![Applying an evolutionary metaheuristic Discovering counter intuitive solutions As expected IC-SPEA2 returned multiple, pareto-optimal strategies Two solutions were of particular interest 1. The feeding strategy that maximised net revenue. 2. The feeding strategy that maximised live weight gain . Intuition suggests that heavy animals should sell for more money [maximum live weight gain] = [maximum net revenue] Yet IC-SPEA2 found a way to maximise net revenue while delivering lighter animals This counter-intuitive result has potential implications for farm sustainability](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-98-2048.jpg)
![Applying an evolutionary metaheuristic Discovering counter intuitive solutions As expected IC-SPEA2 returned multiple, pareto-optimal strategies Two solutions were of particular interest 1. The feeding strategy that maximised net revenue. 2. The feeding strategy that maximised live weight gain . Intuition suggests that heavy animals should sell for more money [maximum live weight gain] = [maximum net revenue] Yet IC-SPEA2 found a way to maximise net revenue while delivering lighter animals This counter-intuitive result has potential implications for farm sustainability](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-99-2048.jpg)
![Applying an evolutionary metaheuristic Discovering counter intuitive solutions As expected IC-SPEA2 returned multiple, pareto-optimal strategies Two solutions were of particular interest 1. The feeding strategy that maximised net revenue. 2. The feeding strategy that maximised live weight gain . Intuition suggests that heavy animals should sell for more money [ maximum live weight gain ] = [ maximum net revenue ] Yet IC-SPEA2 found a way to maximise net revenue while delivering lighter animals This counter-intuitive result has potential implications for farm sustainability](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-100-2048.jpg)
![Applying an evolutionary metaheuristic Discovering counter intuitive solutions As expected IC-SPEA2 returned multiple, pareto-optimal strategies Two solutions were of particular interest 1. The feeding strategy that maximised net revenue. 2. The feeding strategy that maximised live weight gain . Intuition suggests that heavy animals should sell for more money [maximum live weight gain] = [maximum net revenue] Yet IC-SPEA2 found a way to maximise net revenue while delivering lighter animals This counter-intuitive result has potential implications for farm sustainability](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-101-2048.jpg)
![Applying an evolutionary metaheuristic Discovering counter intuitive solutions As expected IC-SPEA2 returned multiple, pareto-optimal strategies Two solutions were of particular interest 1. The feeding strategy that maximised net revenue. 2. The feeding strategy that maximised live weight gain . Intuition suggests that heavy animals should sell for more money [maximum live weight gain] = [maximum net revenue] Yet IC-SPEA2 found a way to maximise net revenue while delivering lighter animals This counter-intuitive result has potential implications for farm sustainability](https://image.slidesharecdn.com/AnIntroductiontoAppliedEvolutionaryMetaheuristics-122710192792-phpapp03/75/An-Introduction-To-Applied-Evolutionary-Meta-Heuristics-102-2048.jpg)










