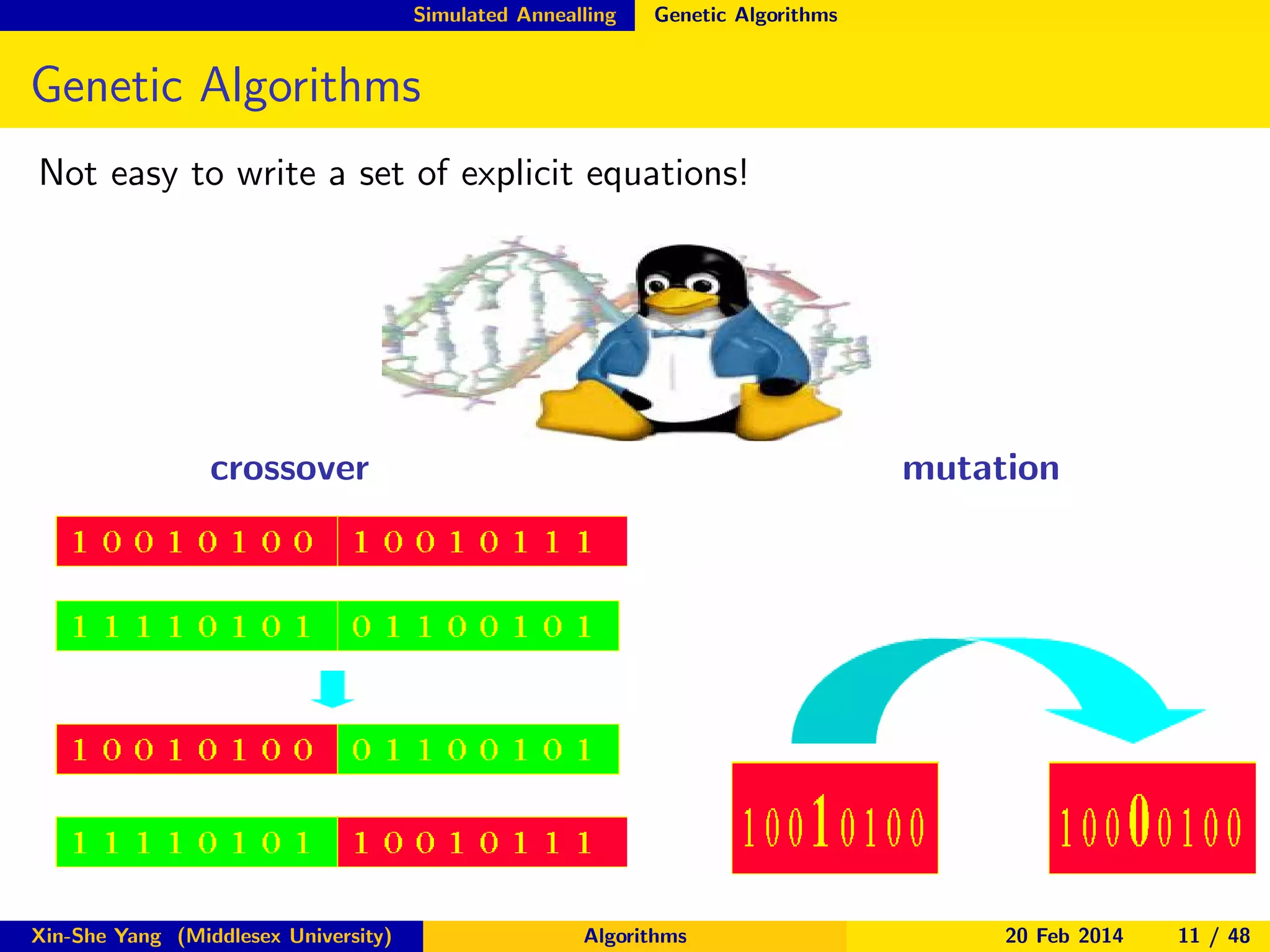
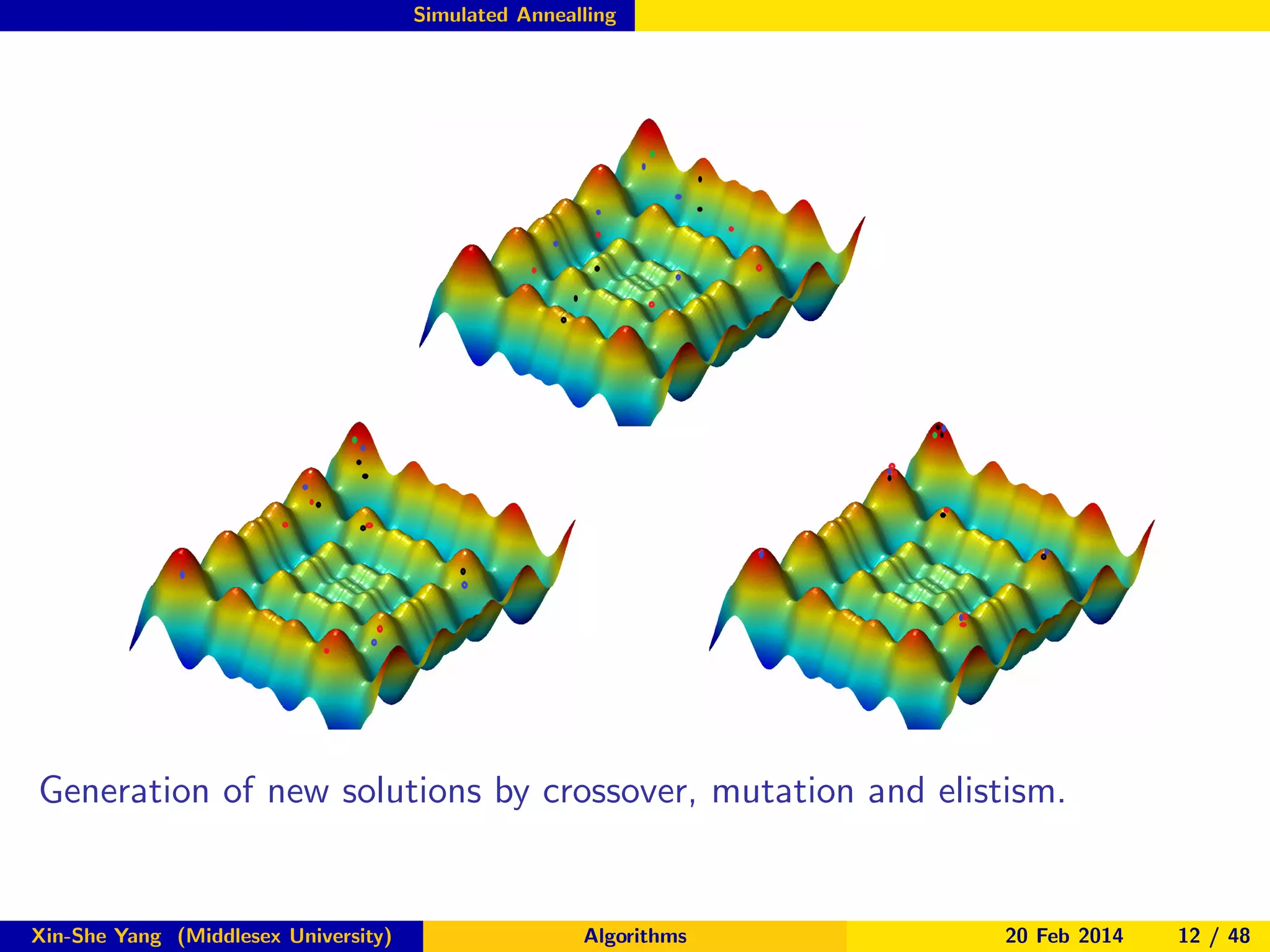
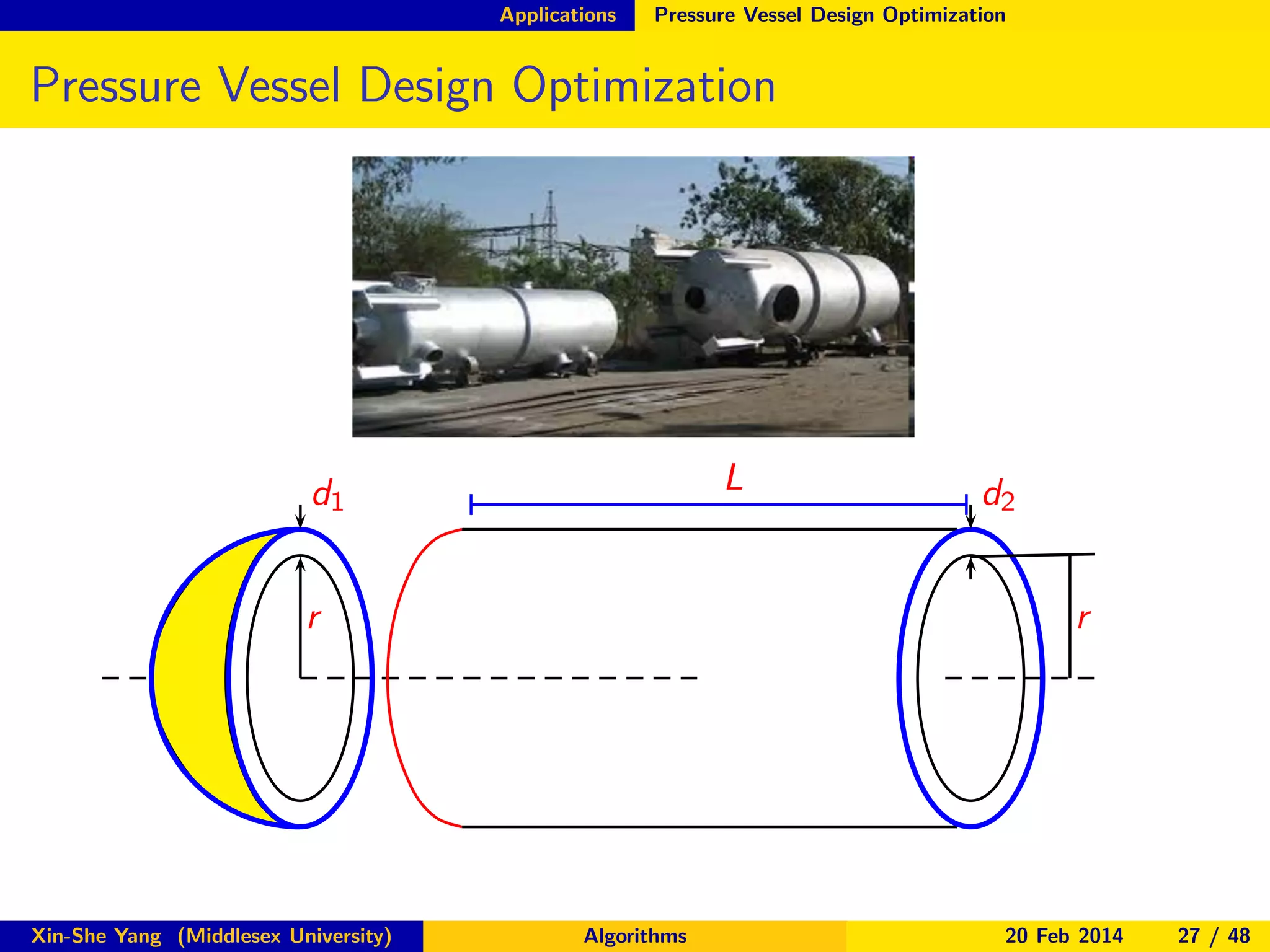
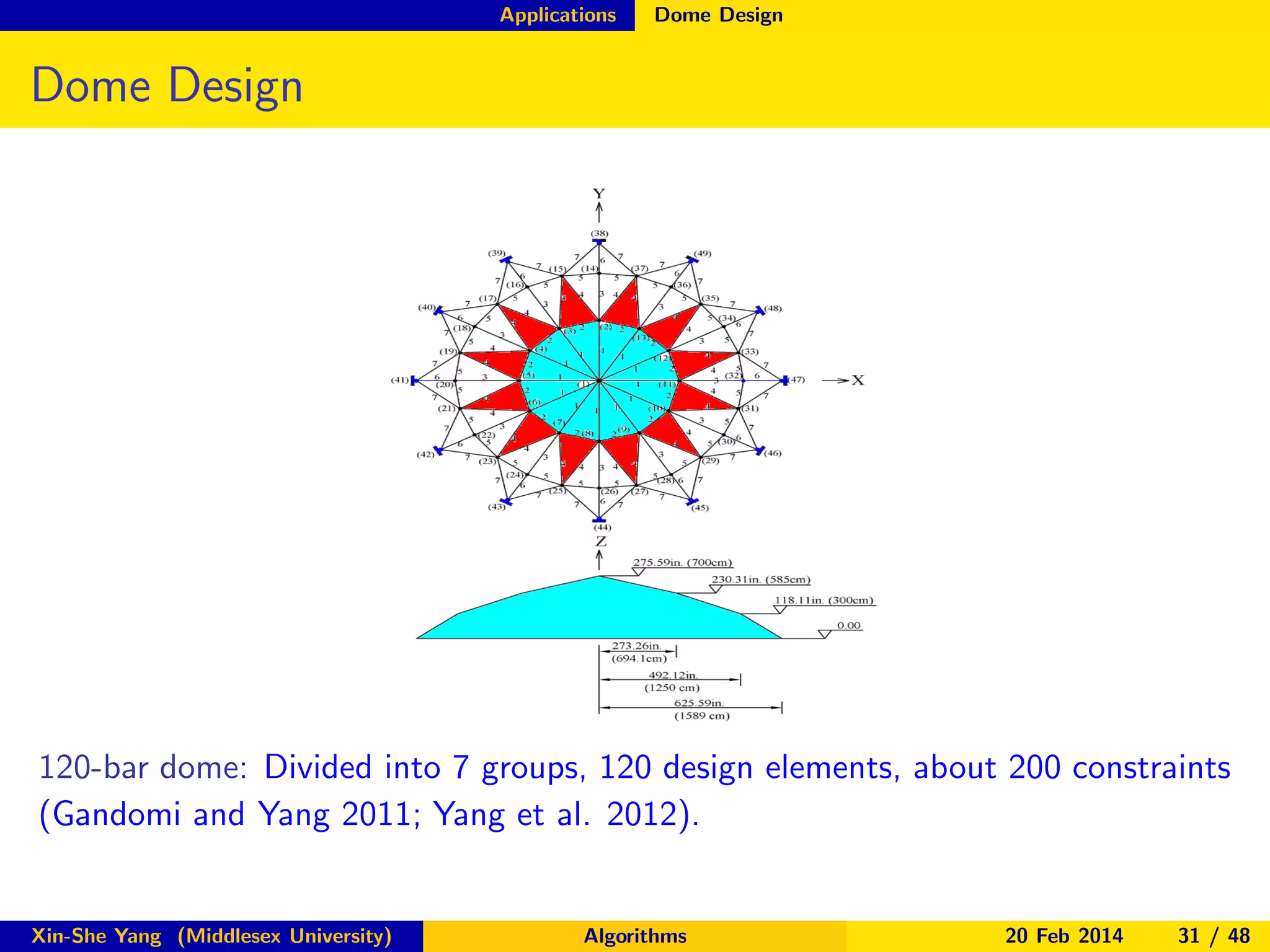
The document discusses nature-inspired optimization algorithms, detailing various types such as genetic algorithms, particle swarm optimization, and simulated annealing. It highlights their applications in engineering design and optimization across multiple disciplines. The seminar covers both theoretical foundations and practical implementations, showcasing how these algorithms improve complex problem-solving through mimicking natural processes.

1. Analysis of Nature-Inspired Optimization Algorithms
Xin-She Yang
School of Science and Technology
Middlesex University
Seminar at Department of Mathematical Sciences
University of Essex
20 Feb 2014
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
1 / 48

2. Overview
Overview
Overview
Introduction
What is an Algorithm?
Nature-Inspired Optimization Algorithms
Applications in Engineering Design
Self-Organization and Optimization Algorithms
Conclusions
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
2 / 48

3. The Essence of an Algorithm
The Essence of an Algorithm
The Essence of an Algorithm
Essence of an Optimization Algorithm
To move to a new, better point x(t+1) from an existing location x(t) .
x(t)
?
x2
x(t+1)
x1
Population-based algorithms use multiple, interacting paths.
Different algorithms
Different strategies/approaches in generating these moves!
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
3 / 48

4. The Essence of an Algorithm
Optimization Algorithms
Optimization Algorithms
Deterministic
Newton’s method (1669, published in 1711), Newton-Raphson
(1690), hill-climbing/steepest descent (Cauchy 1847), least-squares
(Gauss 1795),
linear programming (Dantzig 1947), conjugate gradient (Lanczos et
al. 1952), interior-point method (Karmarkar 1984), etc.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
4 / 48

5. The Essence of an Algorithm
Steepest Descent/Hill Climbing
Steepest Descent/Hill Climbing
Gradient-Based Methods
Use gradient/derivative information – very efficient for local search.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
5 / 48

6. The Essence of an Algorithm
Newton’s Method

xt+1 = xt − H−1 ∇f ,

H=

∂2f
∂x1 2
.
.
.
∂2f
∂xd ∂x1
···
..
.
···
∂2f
∂x1 ∂xd
.
.
.
∂2f
∂xd 2


.

Quasi-Newton
If H is replaced by I, we have
xt+1 = xt − αI∇f (xt ).
Here α controls the step length.
Generation of new moves by gradient.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
6 / 48

7. The Essence of an Algorithm
The Essence of an Algorithm
The Essence of an Algorithm
In essence, an algorithm can be written (mathematically) as
xt+1 = A(xt , α),
For any given xt , the algorithm will generate a new solution xt+1 .
Functional or a Dynamical System?
We can view the above equation as
a functional,
or a dynamical system,
or a Markov chain,
or a self-organizing system.
The behavoir of the system (algorithm) can be controlled by A and its
parameter α.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
7 / 48

8. Nature-Inspired Algorithms
Stochastic/Metaheuristic Algorithms
Stochastic/Metaheuristic Algorithms
Genetic algorithms (1960s/1970s), evolutionary strategy (Rechenberg
& Swefel 1960s), evolutionary programming (Fogel et al. 1960s).
Simulated annealing (Kirkpatrick et al. 1983), Tabu search (Glover
1980s), ant colony optimization (Dorigo 1992), genetic programming
(Koza 1992), particle swarm optimization (Kennedy & Eberhart
1995), differential evolution (Storn & Price 1996/1997), harmony
search (Geem et al. 2001), honeybee algorithm (Nakrani & Tovey
2004), artificial bee colony (Karaboga, 2005).
Firefly algorithm (Yang 2008), cuckoo search (Yang & Deb 2009), bat
algorithm (Yang, 2010), ...
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
8 / 48

9. Simulated Annealling
Simulated Annealling
Simulated Annealling
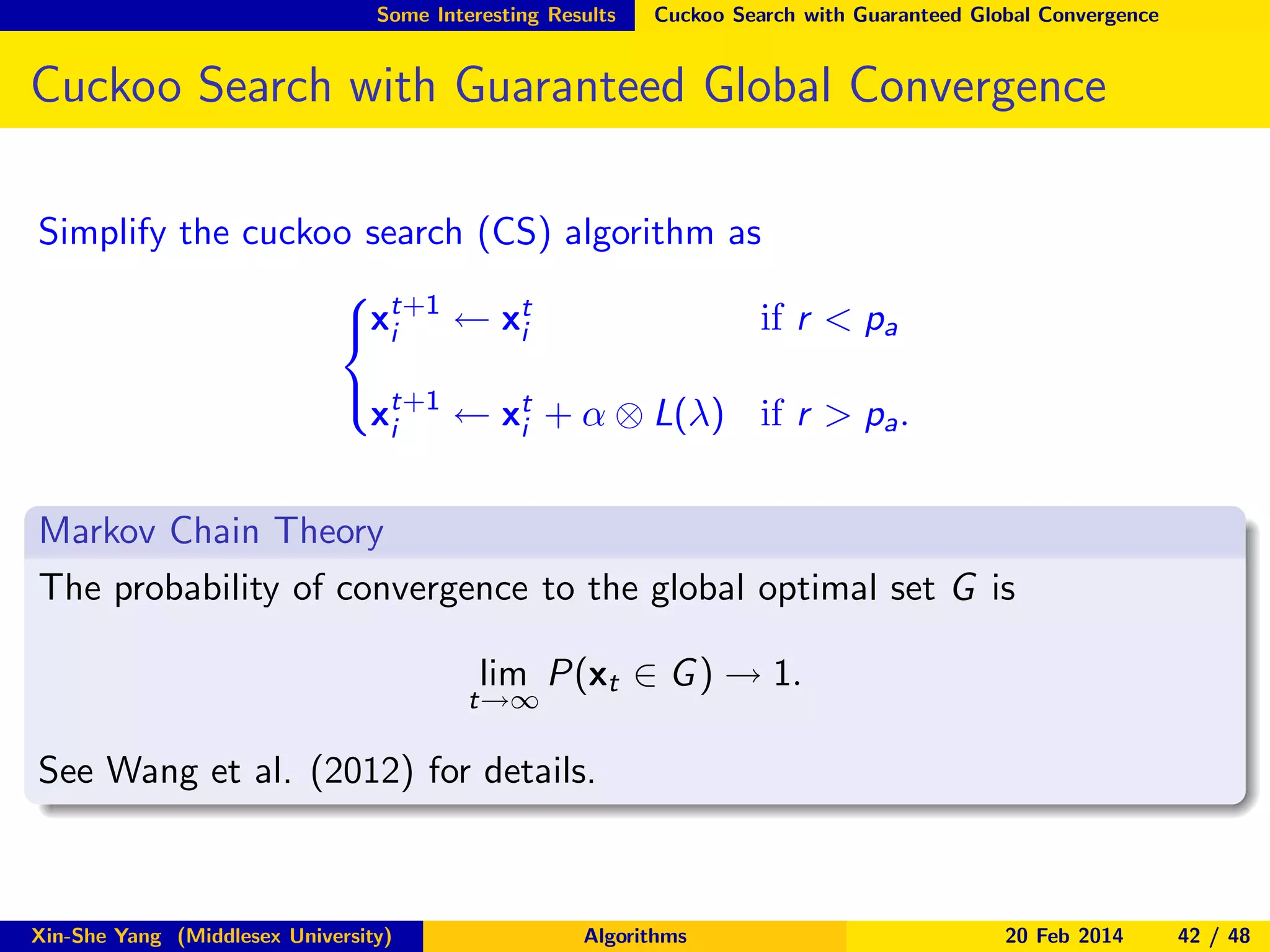
Metal annealing to increase strength =⇒ simulated annealing.
Probabilistic Move: p ∝ exp[−E /kB T ].
kB =Boltzmann constant (e.g., kB = 1), T =temperature, E =energy.
E ∝ f (x), T = T0 αt (cooling schedule) , (0 < α < 1).
T → 0 =⇒ p → 0, =⇒ hill climbing.
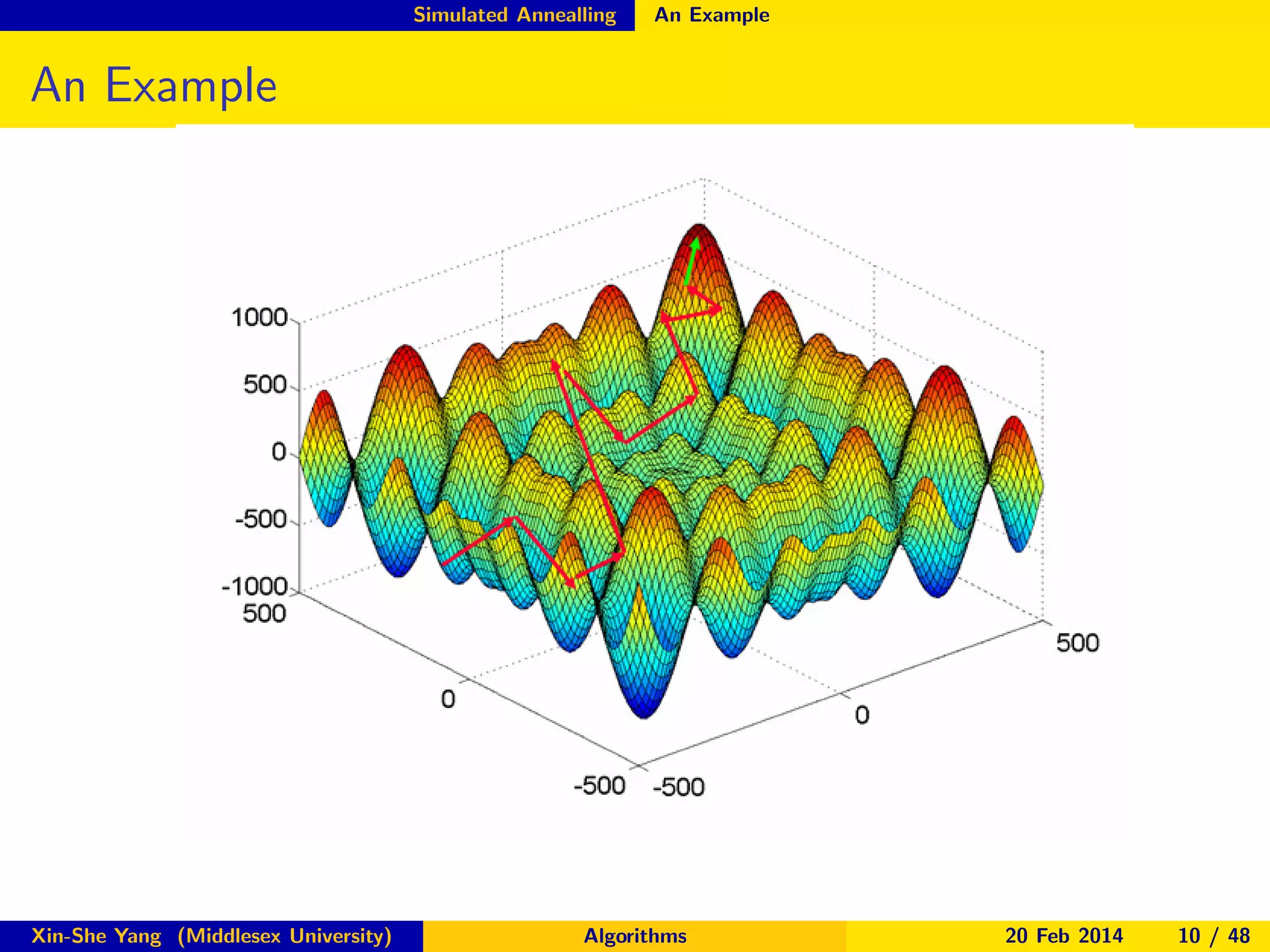
This is equivalent to a random walk
xt+1 = xt + p(xt , α).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
9 / 48

10. Simulated Annealling
An Example
An Example
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
10 / 48

11. Simulated Annealling
Genetic Algorithms
Genetic Algorithms
Not easy to write a set of explicit equations!
crossover
Xin-She Yang (Middlesex University)
mutation
Algorithms
20 Feb 2014
11 / 48

12. Simulated Annealling
Generation of new solutions by crossover, mutation and elistism.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
12 / 48

13. Swarm Intelligence
Swarm Intelligence
Ants, bees, birds, fish ... Simple rules lead to complex behaviour.
Swarming Starlings
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
13 / 48

14. Swarm Intelligence
PSO
PSO
Particle Swarm Optimization (Kennedy and Eberhart, 1995)
xj
g∗
xi
vt+1 = vt + αǫ1 (g∗ − xt ) + βǫ2 (x∗ − xt ),
i
i
i
i
i
xt+1 = xt + vt+1 .
i
i
i
α, β = learning parameters, ǫ1 , ǫ2 =random numbers.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
14 / 48

15. Swarm Intelligence
PSO Demo and Disadvantages
PSO Demo and Disadvantages


xi
vi
t+1


=
1
1
−(αǫ1 + βǫ2 ) 1
PSO Demo
Xin-She Yang (Middlesex University)


xi
vi
t

 +

0
αǫ1
g∗
+
βǫ2 x∗
i
.
Premature convergence
Algorithms
20 Feb 2014
15 / 48

16. Swarm Intelligence
Firefly Algorithm (Yang, 2008)
Firefly Algorithm (Yang, 2008)
Firefly Behaviour and Idealization
Fireflies are unisex and brightness varies with distance.
Less bright ones will be attracted to bright ones.
If no brighter firefly can be seen, a firefly will move randomly.
2
xt+1 = xt + β0 e −γrij (xj − xi ) + α ǫt .
i
i
i
Generation of new solutions by random walk and attraction.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
16 / 48

17. Swarm Intelligence
What is FA so efficient?
What is FA so efficient?
Advantages of Firefly Algorithm
Automatically subdivide the whole population into subgroups, and
each subgroup swarms around a local mode/optimum.
Control modes/ranges by varying γ.
Control randomization by tuning parameters such as α.
Suitable for multimodal, nonlinear, global optimization problems.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
17 / 48

18. Swarm Intelligence
Variants of Firefly Algorithm
Variants of Firefly Algorithm
About 1400 papers about firefly algorithm since 2008. Its literature is
dramatically expanding.
Variants for specific applications:
Continuous optimization, mixed integer programming, ...
Discrete firefly algorithm for scheduling, travelling-salesman problem,
combinatorial optimization ...
Image processing and compression ...
Clustering, classifications and feature selection ...
Chaotic firefly algorithm ...
Hybrid firefly algorithm with other algorithms ...
Multiobjective firefly algorithm.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
18 / 48

19. Swarm Intelligence
Cuckoo Breeding Behaviour
Cuckoo Breeding Behaviour
Evolutionary Advantages
Dumps eggs in the nests of host birds and let these host birds raise their
chicks.
Cuckoo Video (BBC)
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
19 / 48

20. Swarm Intelligence
Cuckoo Search (Yang and Deb, 2009)
Cuckoo Search (Yang and Deb, 2009)
Cuckoo Behaviour and Idealization
Each cuckoo lays one egg (solution) at a time, and dumps its egg in a
randomly chosen nest.
The best nests with high-quality eggs (solutions) will carry out to the
next generation.
The egg laid by a cuckoo can be discovered by the host bird with a
probability pa and a nest will then be built.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
20 / 48

21. Swarm Intelligence
Cuckoo Search
Cuckoo Search
Local random walk:
xt+1 = xt + s ⊗ H(pa − ǫ) ⊗ (xt − xt ).
k
i
j
i
[xi , xj , xk are 3 different solutions, H(u) is a Heaviside function, ǫ is a
random number drawn from a uniform distribution, and s is the step size.
Global random walk via L´vy flights:
e
xt+1 = xt + αL(s, λ),
i
i
L(s, λ) =
λΓ(λ) sin(πλ/2) 1
, (s ≫ s0 ).
π
s 1+λ
Generation of new moves by L´vy flights, random walk and elitism.
e
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
21 / 48

22. Swarm Intelligence
CS Demo: Highly Efficient!
CS Demo: Highly Efficient!
About 1000 papers about cuckoo search since 2009. Its literature is
dramatically expanding.
[See X. S. Yang, Cuckoo Search and Firefly Algorithm: Theory and Applications,
Springer, (2013).]
CS Demo
Xin-She Yang (Middlesex University)
Efficient search with a focus
Algorithms
20 Feb 2014
22 / 48

23. Swarm Intelligence
Bat Algorithm (Yang, 2010)
Bat Algorithm (Yang, 2010)
BBC Video
Microbats use echolocation for hunting
Ultrasonic short pulses as loud as 110dB with a short period of 5 to
20 ms. Frequencies of 25 kHz to 100 kHz.
Speed up pulse-emission rate and increase loudness when homing at a
prey.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
23 / 48

24. Swarm Intelligence
Bat Algorithm
Bat Algorithm
Acoustics of bat echolocation
v
λ = ∼ 2 mm to 14 mm.
f
Rules used in the bat algorithm:
fi = fmin + (fmax − fmin )β,
vt+1 = vit + (xt − x∗ )fi ,
i
i
β ∈ [0, 1],
xt+1 = xt + vt .
i
i
i
Variations of Loudness and Pulse Rate
At+1 ← αAt ,
i
i
α ∈ (0, 1],
rit+1 = ri0 [1 − exp(−γt)].
There are about 240 papers since 2010.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
24 / 48

25. Swarm Intelligence
Other Algorithms
Other Algorithms
Genetic algorithms
Differential evolution
Artificial immune system
Harmony search
Memetic algorithm
...
Reviews
Yang, X. S., Engineering Optimization: An Introduction with
Metaheuristic Applications, John Wiley & Sons, (2010).
Yang, X. S., Nature-Inspired Metaheuristic Algorithms, Luniver Press,
(2008).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
25 / 48

26. Applications
Applications
Applications
Design optimization: structural engineering, product design ...
Scheduling, routing and planning: often discrete, combinatorial
problems ...
Applications in almost all areas (e.g., finance, economics, engineering,
industry, ...)
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
26 / 48

27. Applications
Pressure Vessel Design Optimization
Pressure Vessel Design Optimization
L
d1
r
Xin-She Yang (Middlesex University)
d2
r
Algorithms
20 Feb 2014
27 / 48

28. Applications
Pressure Vessel Design
Pressure Vessel Design
This is a well-known test problem for optimization (e.g., see Cagnina et al.
2008) and it can be written as
2
2
minimize f (x) = 0.6224d1 rL + 1.7781d2 r 2 + 3.1661d1 L + 19.84d1 r ,

g1 (x) = −d1 + 0.0193r ≤ 0


g2 (x) = −d2 + 0.00954r ≤ 0
subject to
g3 (x) = −πr 2 L − 4π r 3 + 1296000 ≤ 0

3

g4 (x) = L − 240 ≤ 0.
The simple bounds are
0.0625 ≤ d1 , d2 ≤ 99 × 0.0625,
10.0 ≤ r ,
L ≤ 200.0.
The best solution (Yang, 2010; Gandomi and Yang, 2011)
f∗ = 6059.714,
Xin-She Yang (Middlesex University)
x∗ = (0.8125, 0.4375, 42.0984, 176.6366).
Algorithms
20 Feb 2014
28 / 48

29. Applications
Speed Reducer/Gear Box Design
Speed Reducer/Gear Box Design
Mixed-Integer Programming:
Continuous variables and integers.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
29 / 48

30. Applications
2
2
f (x1 , x2 , x3 , x4 , x5 , x6 , x7 ) = 0.7854x1 x2 (3.3333x3 + 14.9334x3 − 43.0934)
2
2
3
3
2
2
−1.508x1 (x6 + x7 ) + 7.4777(x6 + x7 ) + 0.7854(x4 x6 + x5 x7 ),
subject to
27
− 1 ≤ 0,
2
x1 x2 x3
3
1.93x
g3 = x x d4 − 1 ≤ 0,
4
2 3 1
1
g5 = 110x 3 ( 745x4 )2 + 16.9 × 106 − 1 ≤ 0,
hx3
6
745x5 2
1
g6 = 85x 3 ( hx3 ) + 157.5 × 106 − 1 ≤ 0,
7
2x
g7 = x403 − 1 ≤ 0,
x1
g9 = 12x2 − 1 ≤ 0,
7 +1.9
g11 = 1.1xx5
− 1 ≤ 0.
g1 =
g2 =
g4 =
397.5
2 2
x1 x2 x3
3
1.93x5
4
x2 x3 d2
− 1 ≤ 0,
− 1 ≤ 0,
g8 = 5x12 − 1 ≤ 0,
x
6 +1.9
g10 = 1.5xx4
− 1 ≤ 0,
Simple bounds are 2.6 ≤ x1 ≤ 3.6, 0.7 ≤ h ≤ 0.8, 17 ≤ x3 ≤ 28,
7.3 ≤ x4 ≤ 8.3, 7.8 ≤ x5 ≤ 8.3, 2.9 ≤ x6 ≤ 3.9, and 5.0 ≤ x7 ≤ 5.5. z
must be integers.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
30 / 48

31. Applications
Dome Design
Dome Design
120-bar dome: Divided into 7 groups, 120 design elements, about 200 constraints
(Gandomi and Yang 2011; Yang et al. 2012).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
31 / 48

32. Applications
Tower Design
Tower Design
26-storey tower: 942 design elements, 244 nodal links, 59 groups/types, > 4000
nonlinear constraints
(Yang et al. 2011; Gandomi & Yang 2012).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
32 / 48

33. Applications
Car Design
Car Design
Design better, safer and energy-efficient cars
Minimize weight, low crash deflection (< 32 mm), lower impact force (< 4
kN), .... Even a side barrier has 11 design variables!
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
33 / 48

34. The Essence of an Algorithm
The Essence of an Algorithm
The Essence of an Algorithm
In essence, an algorithm can be written (mathematically) as
xt+1 = A(xt , α),
For any given xt , the algorithm will generate a new solution xt+1 .
Functional or a Dynamical System?
We can view the above equation as
a functional,
or a dynamical system,
or a Markov chain,
or a self-organizing system.
The behavoir of the system (algorithm) can be controlled by A and its
parameter α.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
34 / 48

35. The Essence of an Algorithm
Self-Organization
Self-Organization
Self-organizing systems are everywhere,
physical, chemical, biological, social, artificial ...
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
35 / 48

36. The Essence of an Algorithm
Conditions for Self-Organization
Conditions for Self-Organization
Complex Systems:
Large size, a sufficient number of degrees of freedom,
a huge number of (possible) states S.
Allow the systems to evolve for a long time.
Enough diversity (perturbation, noise, edge of chaos,
far-from-equilibrium).
Selection (unchanging laws etc).
That is
α(t)
S(θ) −→ S(π).
S + α forms a larger system, so S is self-organizing, driven by α(t).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
36 / 48

37. The Essence of an Algorithm
Optimization Process
Optimization Process
Optimization is a process to find an optimal solution (state), from all
possible states of a problem objective g , carried out by an algorithm A and
driven by tuning some algorithm-dependent parameters p(t) = (p1 , ..., pk ).
An Algorithm = Iterative Procedure
xt+1 = A(xt , p(t)).
Optimization
A(t)
g (xt=0 ) −→ g (x∗ ).
An algorithm has to use information of problem states during iterations
(e.g., gradient information, selection of the fittest, best solutions etc).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
37 / 48

38. The Essence of an Algorithm
Similarities Between Self-Organization and Optimization
Similarities Between Self-Organization and Optimization
Self-organization:
Noise, perturbation =⇒ diversity.
Selection mechanism =⇒ structure.
Far-from-equilibrium and large perturbation =⇒ potentially faster to
re-organize.
Optimization Algorithms:
Randomization, stochastic components, exploration
=⇒ to escape local optima.
Selection and exploitation =⇒ convergence & optimal solutions.
High-degrees of randomization
=⇒ more likely to reach global optimality (but may be slow).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
38 / 48

39. The Essence of an Algorithm
But there are significant differences!
But there are significant differences!
Self-Organization:
Avenues to self-organization may be unclear.
Time may not be important.
Optimization (especially metaheuristics):
How to make an algorithm converge is very important.
Speed of convergence is crucial
(to reach truly global optimality with the minimum computing
efforts).
However, we lack good theories to understand either self-organization or
metaheuristic optimization.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
39 / 48

40. The Essence of an Algorithm
Multi-Agent System (Swarm Intelligence?)
Multi-Agent System (Swarm Intelligence?)
For a multi-agent system or a swarm, an algorithm can be considered as a
set of interacting Markov chain or a complex dynamical system
t+1
 t
x1
x1
 x2 
 x2 
 
 
= A[x1 , ..., xn ; ǫ1 , ..., ǫm ; p1 (t), ..., pk (t)] .  .
 . 
 . 
 . 
.
.

xn
xn
A population of solutions xt+1 (i = 1, ..., n) are generated from xt ,
i
i
controlled by k parameters and m random numbers.
In principle, the behaviour of an algorithm is controlled by the eigenvalues
of A, but in practice, it is almost impossible to figure out the eigenvalues
(apart from very simple/rare cases).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
40 / 48

41. Some Interesting Results
Genetic Algorithms
Genetic Algorithms
For a binary genetic algorithm with p0 = 0.5 with n chromosomes of length
m, the probability of (premature) convergence at any time/iteration t is
P(t, m) = 1 −
2
6p0 (1 − p0 )
1−
n
n
t m
.
For a population of n = 40, m = 100, t = 100 generations, we have
P(t, m) = − 1
6 × 0.5(1 − 0.5)
2
(1 − )100
40
40
100
≈ 0.978.
For genetic algorithms with a given accuracy ζ, the number of iterations
t(ζ) needed is (possibly converged prematurely)
t(ζ) ≤
ln(1 − ζ)
ln 1 − min[(1 − µ)nL , µnL ]
,
where µ =mutation rate, L =string length, and n =population size.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
41 / 48

42. Some Interesting Results
Cuckoo Search with Guaranteed Global Convergence
Cuckoo Search with Guaranteed Global Convergence
Simplify the cuckoo search (CS) algorithm as
 t+1
if r < pa
xi ← xt
i
 t+1
xi ← xt + α ⊗ L(λ) if r > pa .
i
Markov Chain Theory
The probability of convergence to the global optimal set G is
lim P(xt ∈ G ) → 1.
t→∞
See Wang et al. (2012) for details.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
42 / 48

43. Exploration & Exploitation
Key Components in All Metaheuristics
Key Components in All Metaheuristics
So many algorithms – what are the common characteristics?
What are the key components?
How to use and balance different components?
What controls the overall behaviour of an algorithm?
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
43 / 48

44. Exploration & Exploitation
Exploration and Exploitation
Exploration and Exploitation
Characteristics of Metaheuristics
Exploration and Exploitation, or Diversification and Intensification.
Exploitation/Intensification
Intensive local search, exploiting local information.
E.g., hill-climbing.
Exploration/Diversification
Exploratory global search, using randomization/stochastic components.
E.g., hill-climbing with random restart.
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
44 / 48

45. Exploration & Exploitation
Summary
Summary
Exploration
uniform
search
Ge
net
Best?
Free lunch?
CS
ic
alg
ori
th
SA
PS
O/
FA
EP
/E
A nt
S
/Be
e
ms
NewtonRaphson
Tabu Nelder-Mead
Exploitation
Xin-She Yang (Middlesex University)
Algorithms
steepest
descent
20 Feb 2014
45 / 48

46. Open Problems
Open Problems
Open Problems
Mathematical Analysis: A unified mathematical framework (e.g.,
Markov chain theory, dynamical systems) is needed.
Comparison: What are the best performance measures?
Parameter tuning: How to tune the algorithm-dependent
parameters so that an algorithm can achieve the best performance?
Scalability: Can the algorithms that work for small-scale problems be
directly applied to large-scale problems?
Intelligence: Smart algorithms may be a buzz word, but can truly
intelligent algorithms be developed?
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
46 / 48

47. Open Problems
Bibliography
Bibliography
Xin-She Yang, Nature-Inspired Optimization Algorithms, Elsevier, (2014).
Xin-She Yang, Cuckoo Search and Firefly Algorithm: Theory and Applications, Springer,
(2013).
Xin-She Yang and Suash Deb, Multiobjective cuckoo search for design optimization,
Computers & Operations Research, 40(6), 1616–1624 (2013).
A. H. Gandomi, X. S. Yang, S. Talatahari, S. Deb, Coupled eagle strategy and differential
evolution for unconstrained and constrained global optimization, Computers &
Mathematics with Applications, 63(1), 191–200 (2012).
A. H. Gandomi, G. J. Yun, X. S. Yang, S. Talatahari, Chaos-enhanced accelerated particle
swarm optimization, Communications in Nonlinear Science and Numerical Simulation,
18(2), 327–340 (2013).
X. S. Yang and S. Deb, Two-stage eagle strategy with differential evolution, Int. Journal
of Bio-Inspired Computation, 4(1), 1–5 (2012).
X. S. Yang, Multiobjective firefly algorithm for continuous optimization, Engineering with
Computers, 29(2), 175–184 (2013).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
47 / 48

48. Open Problems
Thank you
Thank you
Xin-She Yang, Z. H. Cui, R. B. Xiao, A. H. Gandomi, M. Karamanoglu, Swarm
Intelligence and Bio-Inspired Computation: Theory and Applications, Elsevier, (2013).
Xin-She Yang, A. H. Gandomi, S. Talatahari, A. H. Alavi, Metaheuristics in Water,
Geotechnical and Transport Engineering, Elsevier, (2012).
A. H. Gandomi, Xin-She Yang, A. H. Alavi, Mixed variable structural optimization using
firefly algorithm, Computers & Structures, vol. 89, no. 23, 2325–2336 (2011).
Xin-She Yang and A. H. Gandomi, Bat algorithm: a novel approach for global engineering
optimization, Engineering Computations, vol. 29, no. 5, 464–483 (2012).
Xin-She Yang, A new metaheuristic bat-inspired algorithm, in: Nature Inspired
Cooperative Strategies for Optimization (NISCO 2010) (Eds. J. R. Gonzalez et al.),
Studies in Computational Intelligence (SCI 284), Springer, pp. 65–74 (2010).
Xin-She Yang, Artificial Intelligence, Evolutionary Computing and Metaheuristics — In the
Footsteps of Alan Turing, Studies in Computational Intelligence (SCI 427), Springer
Heidelberg, (2013).
Xin-She Yang (Middlesex University)
Algorithms
20 Feb 2014
48 / 48