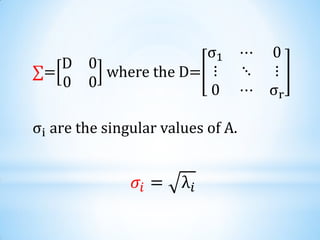The document discusses several linear algebra concepts and their applications to image processing including:
1) Image processing which converts an image signal into a physical image using processes like storing digital photographs in files and using software to manipulate images.
2) Diagonalization of symmetric matrices which finds a corresponding diagonal matrix D for a real symmetric matrix A using eigenvectors.
3) Quadratic forms which express the value of a vector x when operated on by a matrix A as xT Ax.
4) Applications of these concepts like the singular value decomposition and eigendecomposition are used in image processing and analyzing pixel neighborhoods in images.