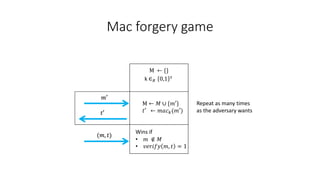
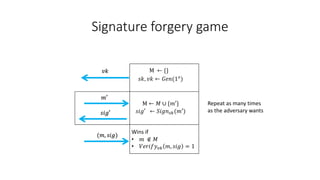
The document discusses digital signatures and signature schemes. It defines a digital signature as allowing the holder of a secret key to sign a document so that anyone with the public verification key can verify the signature is valid. It describes the basic structure of a digital signature scheme including key generation, signing, and verification. It compares digital signature schemes to message authentication codes and discusses how signatures provide non-repudiation while MACs do not. It also covers the security properties of correctness and unforgeability for digital signature schemes.