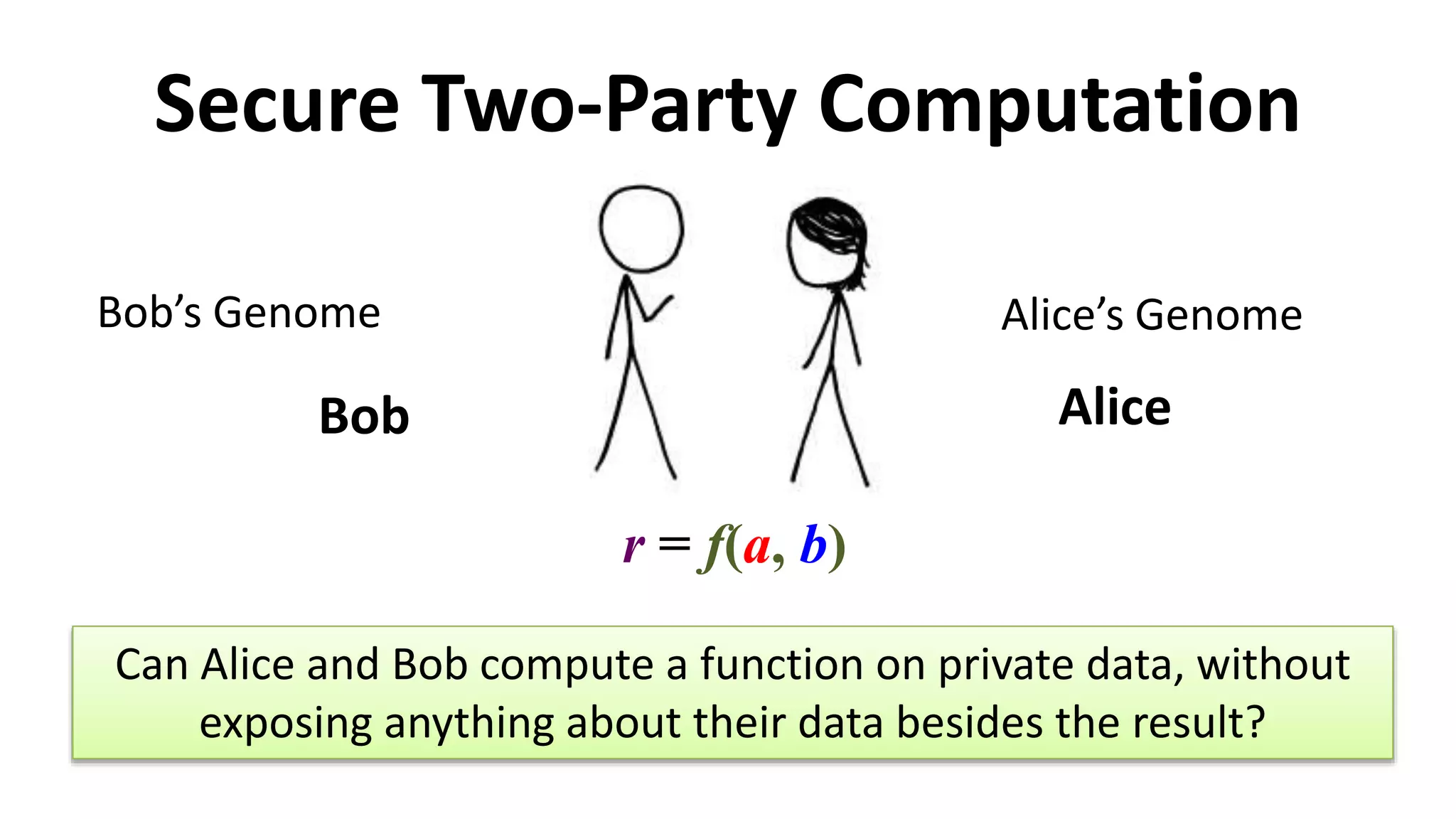
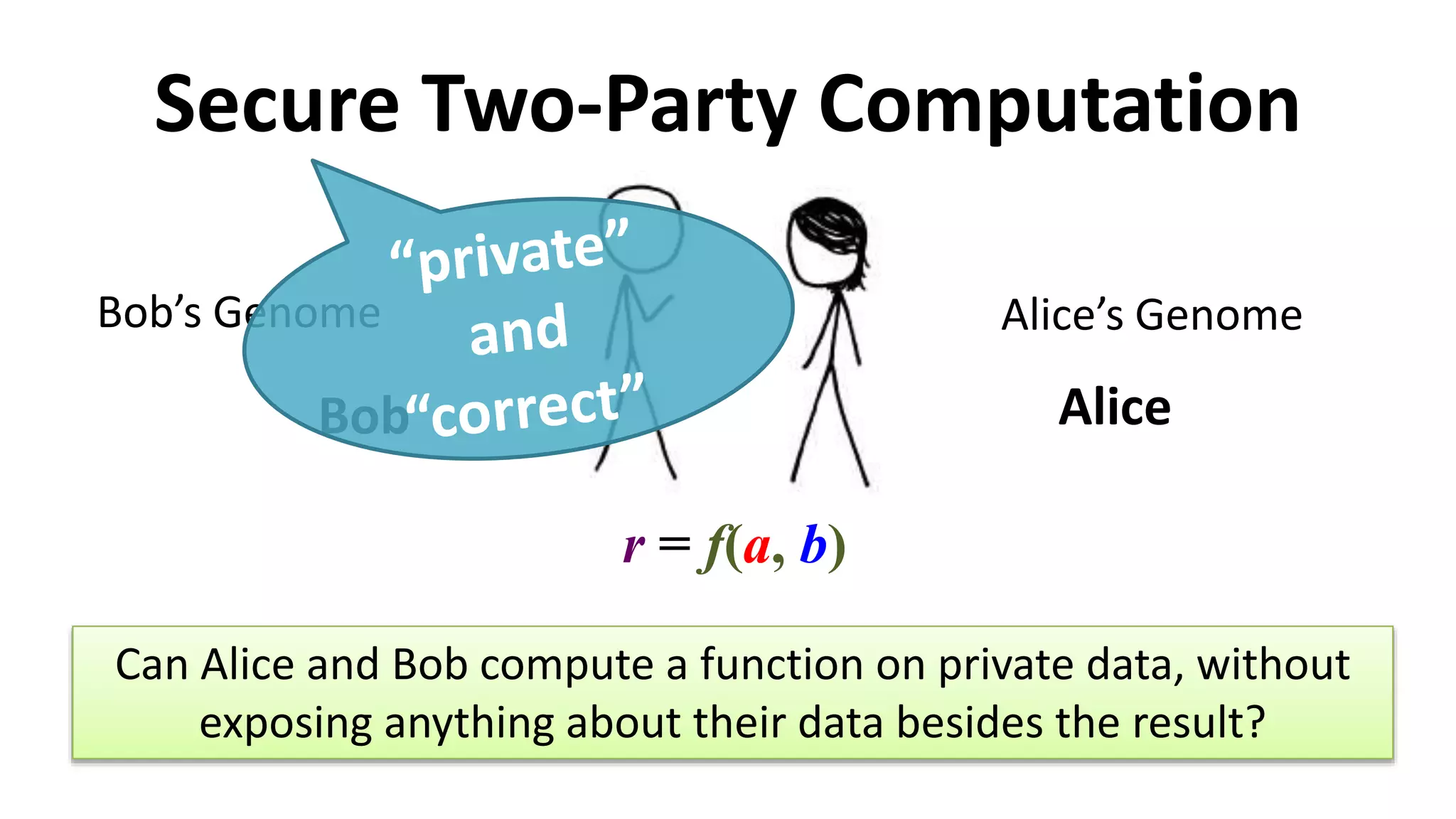
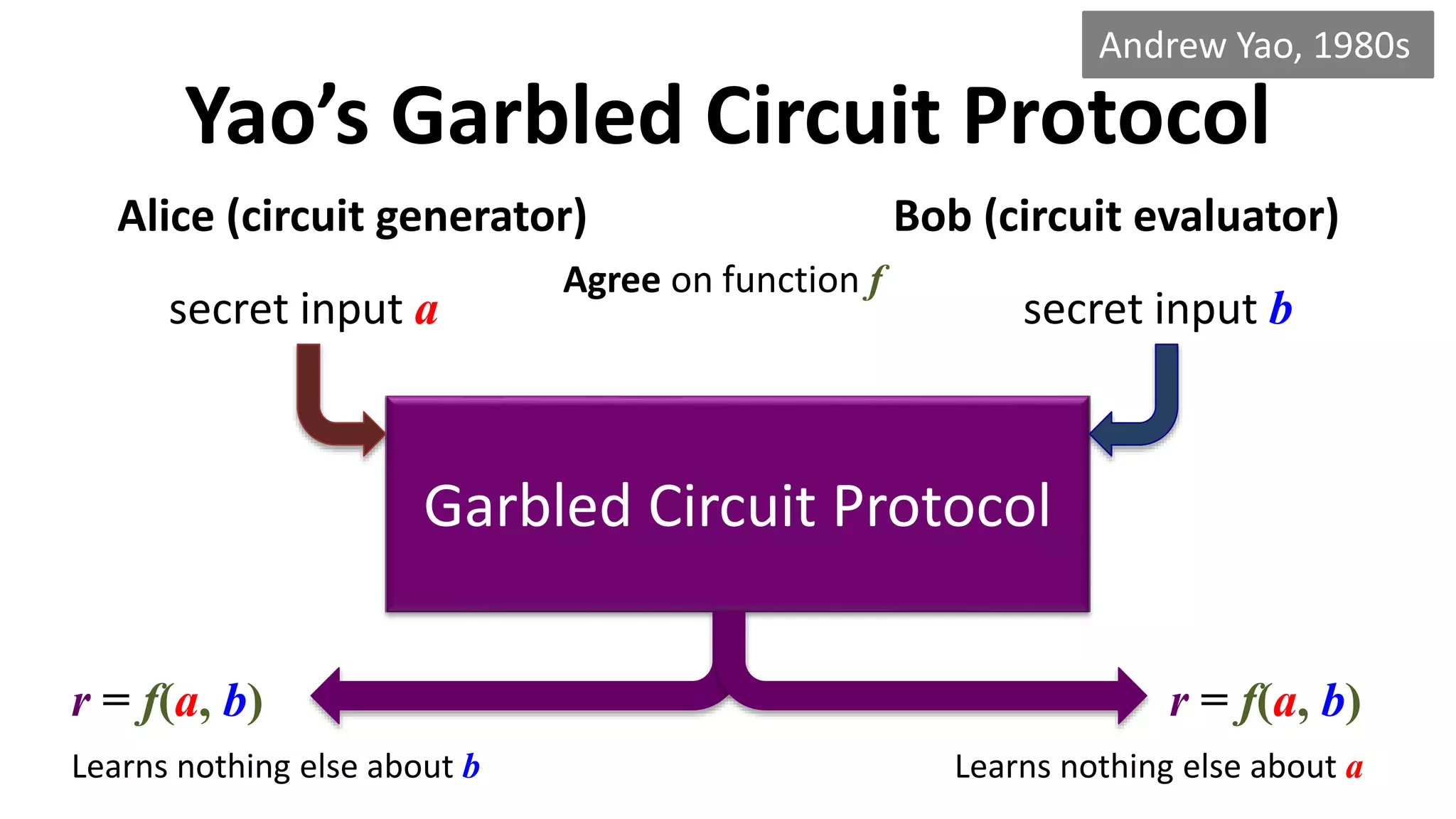
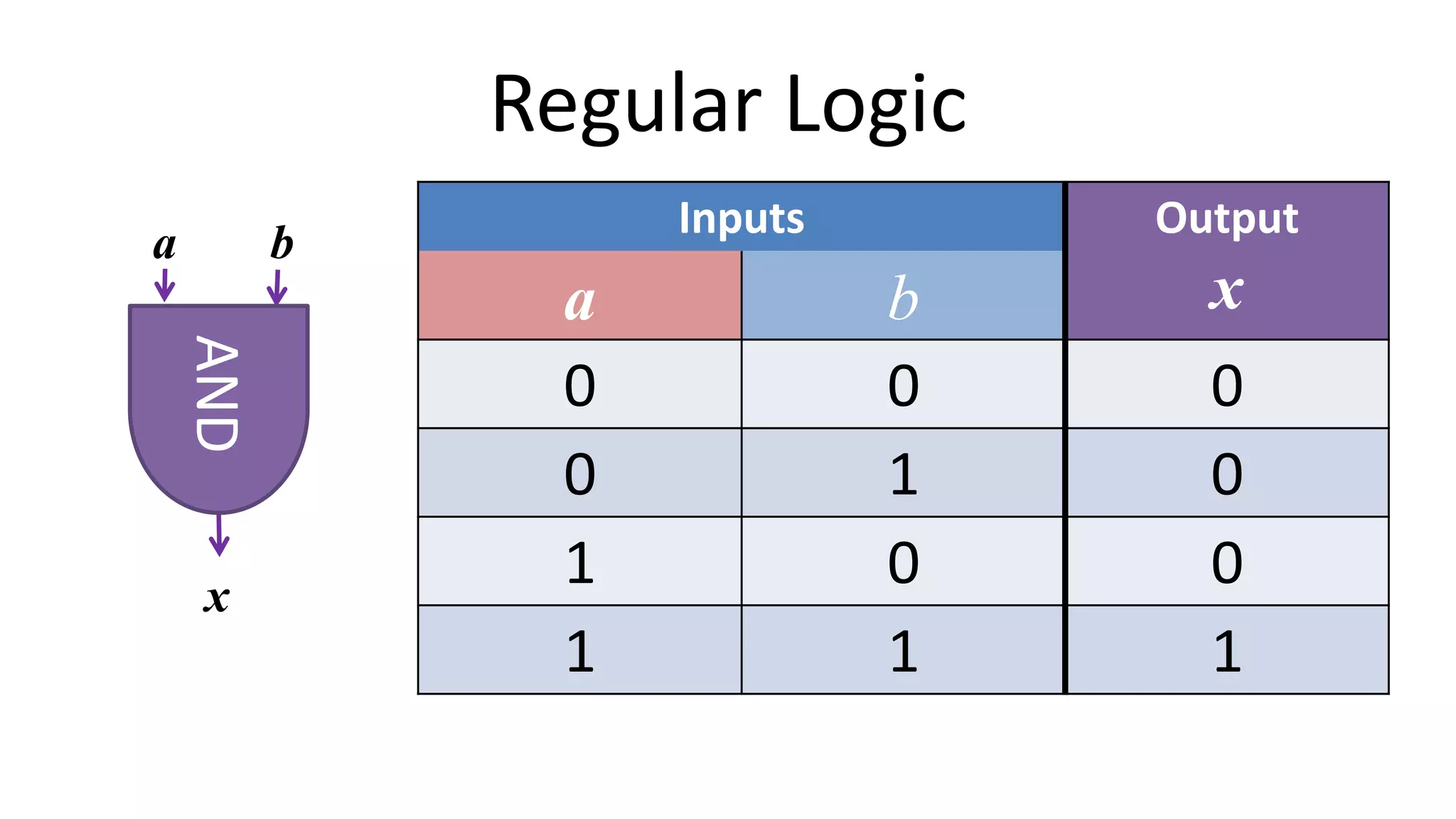
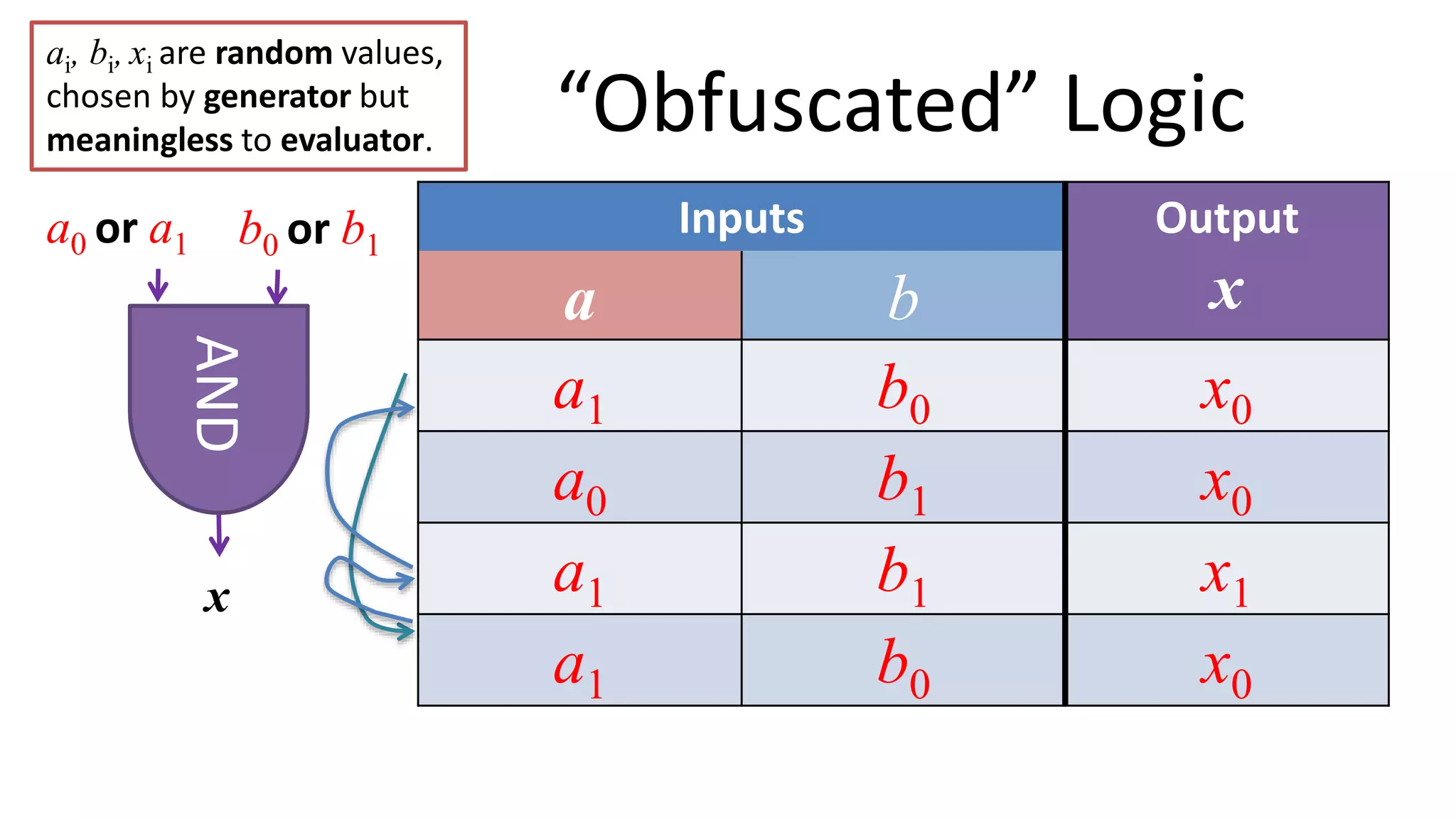
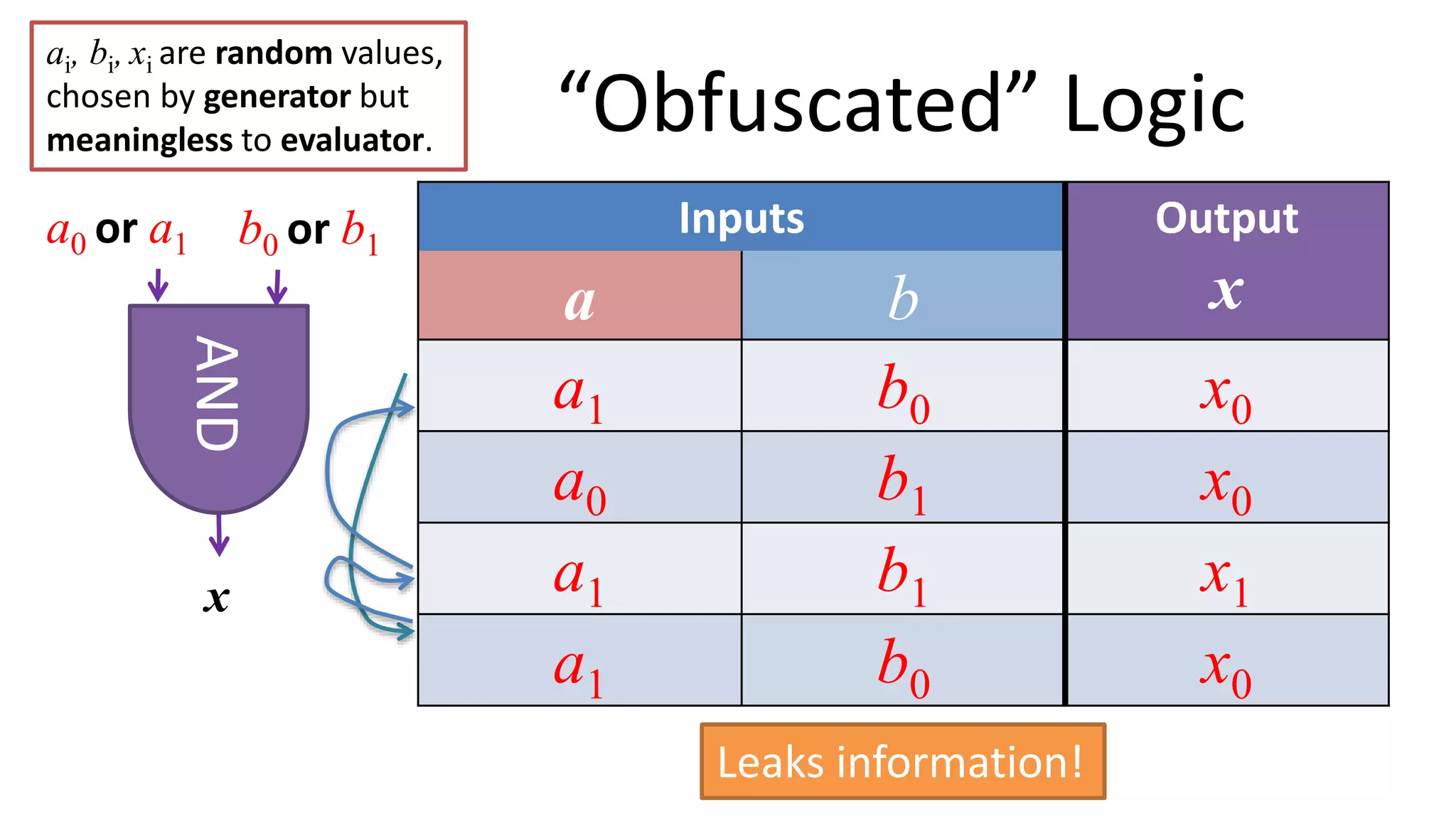
The document discusses multi-party computation techniques, particularly focusing on secure two-party computation protocols like Yao's garbled circuit. It elaborates on the mechanics of these protocols, including how they can process private data without disclosing it and outlines various applications such as personalized medicine and machine learning. Additionally, it presents advancements and efficiency improvements in garbled circuits, addressing security concerns and computational overhead.

![AliceBob
Genome Compatibility
Protocol
“Genetic Dating”
Genetic
Matchr
WARNING!
Reproduction not
recommended
Your offspring
would have
good immune
systems!
processing…Start
[Don’t sue us.]
Genetic
Matchr
WARNING!
Reproduction not
recommended
Your offspring
would have
good immune
systems!
processing…Start
[Don’t sue us.]
(De)Motivating
Application](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-3-2048.jpg)
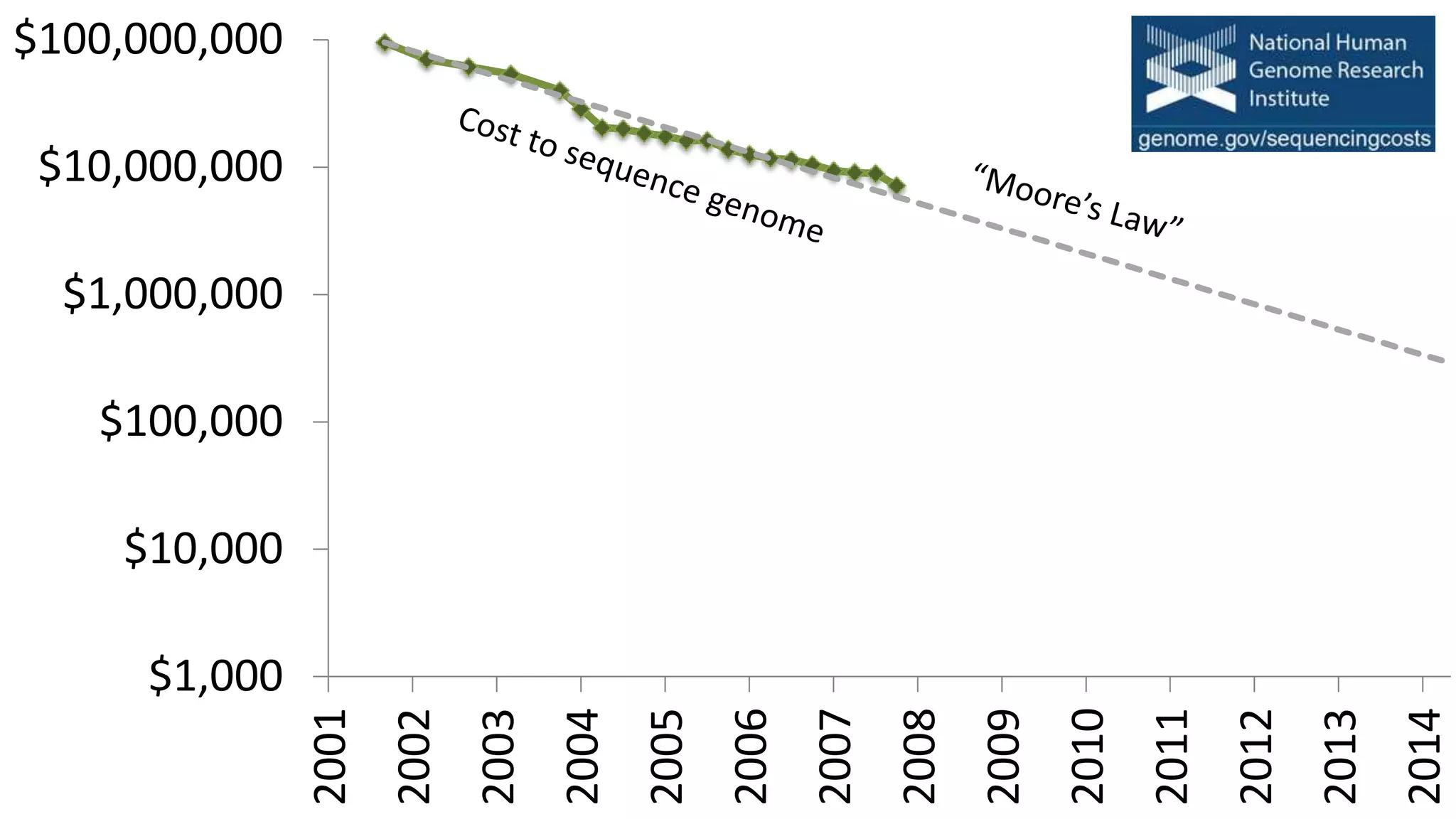
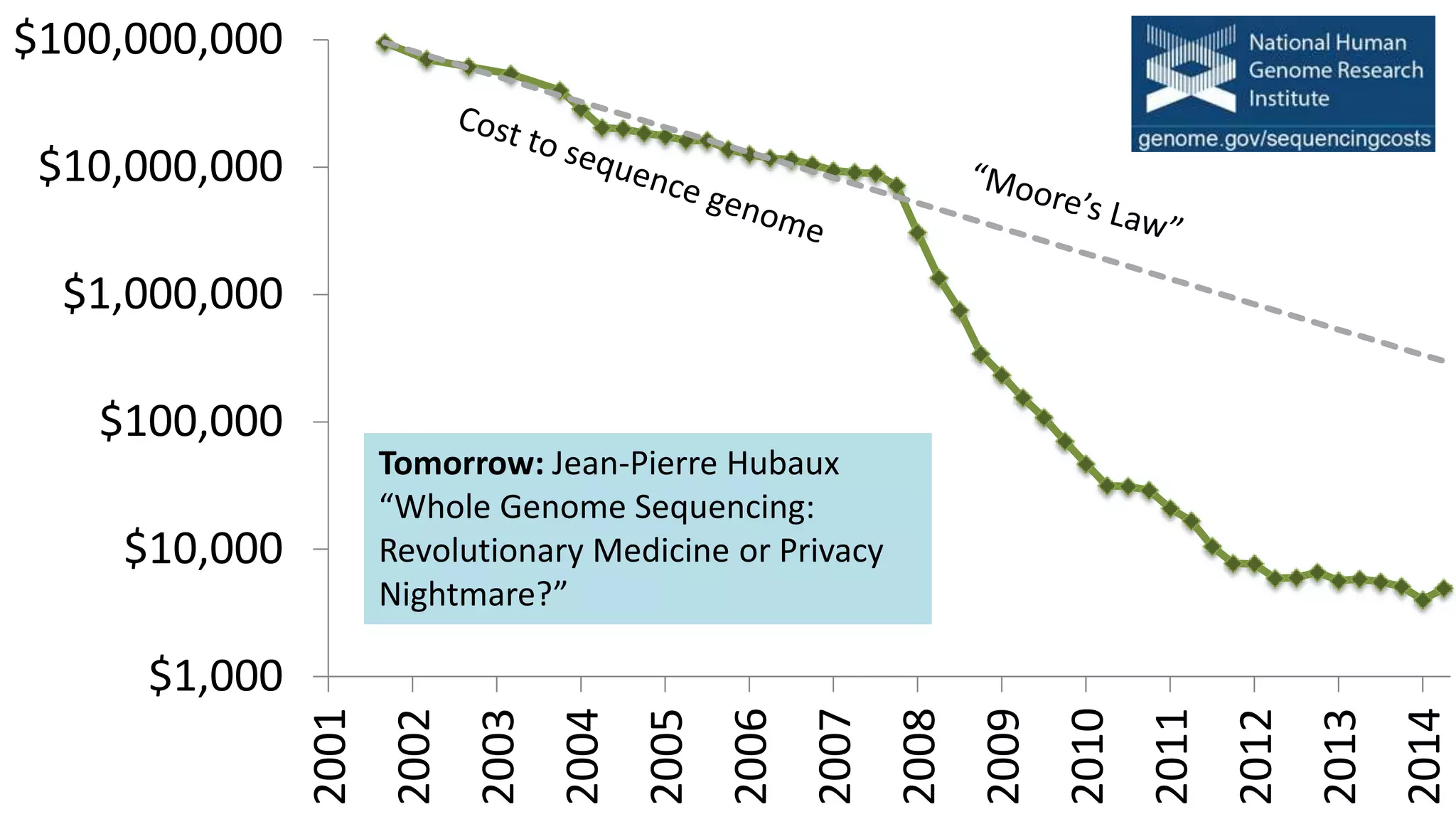





![$1,000
$10,000
$100,000
$1,000,000
$10,000,000
$100,000,000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
[Fairplay, USENIX Sec 2004]
>$1M
Estimated cost of 10k x 10k Smith-Waterman, 4T gates](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-19-2048.jpg)
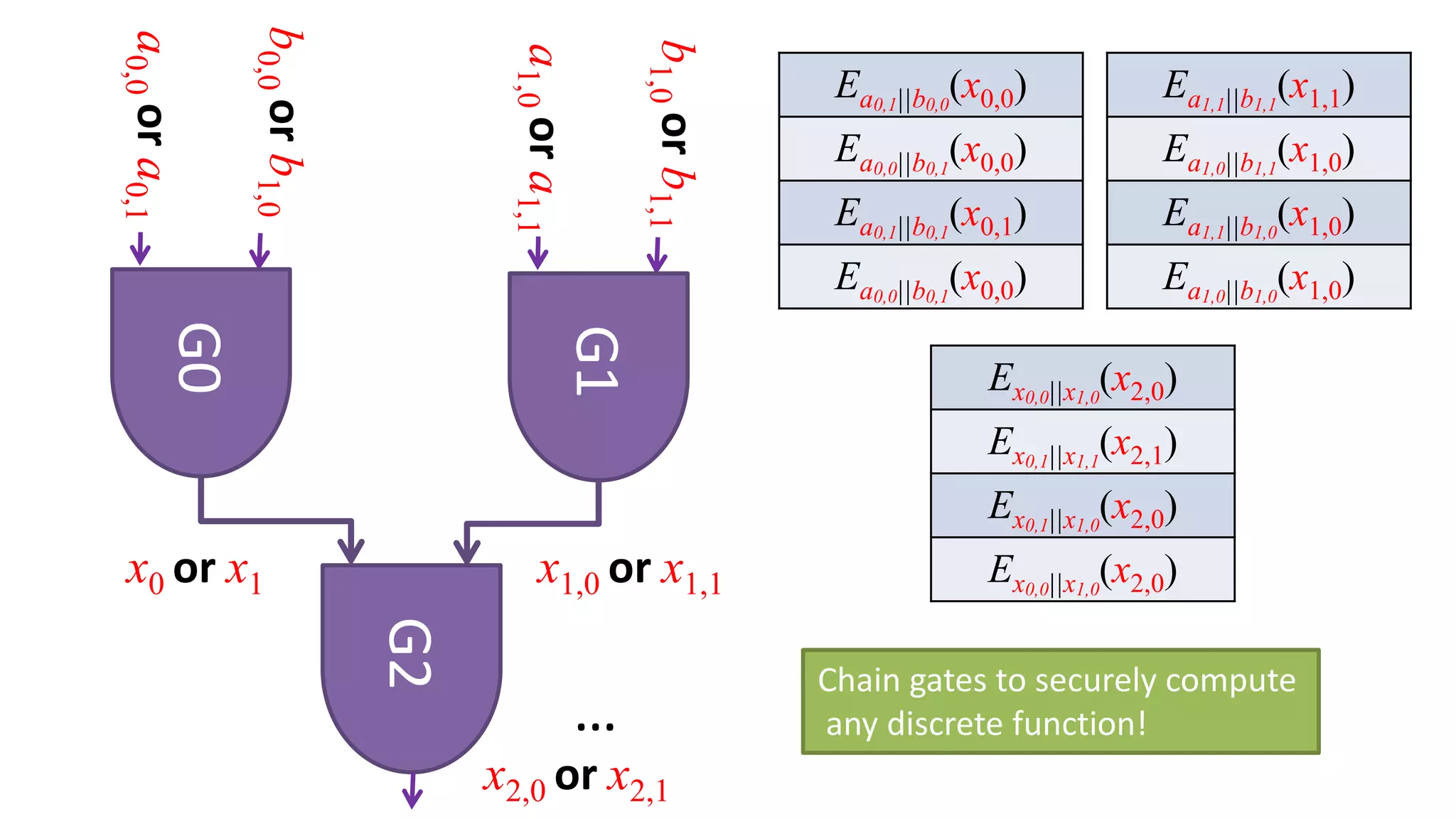
![for (i = 1; i <= n1; ++i) {
for(j = 1; j <= n2; ++j) {
Accum temp = acMin (dp[i][j-1], dp[i-1][j]);
obliv bool d = true;
obliv if (acLessEq(dp[i-1][j-1], temp)) {
acCopy(&temp, &dp[i-1][j-1]);
d = (s1[i-1] != s2[j-1]);
}
ScalingMPC
Gate Execution
Protocols
Ea0,1||b0,0
(x0,0)
Ea0,0||b0,1
(x0,0)
Ea0,1||b0,1
(x0,1)
Ea0,0,|b0,1
(x0,0)
Circuit Construction
Private Biometrics
[NDSS 2011]
Machine Learning [S&P 2013]
Personalized Medicine,
Medical Research
[USENIX Sec 2011]
Private Set Intersection
[NDSS 2012]
Obliv-C](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-20-2048.jpg)
![for (i = 1; i <= n1; ++i) {
for(j = 1; j <= n2; ++j) {
Accum temp = acMin (dp[i][j-1], dp[i-1][j]);
obliv bool d = true;
obliv if (acLessEq(dp[i-1][j-1], temp)) {
acCopy(&temp, &dp[i-1][j-1]);
d = (s1[i-1] != s2[j-1]);
}
ScalingMPC
Gate Execution
Protocols
Ea0,1||b0,0
(x0,0)
Ea0,0||b0,1
(x0,0)
Ea0,1||b0,1
(x0,1)
Ea0,0,|b0,1
(x0,0)
Circuit Construction
Private Biometrics
[NDSS 2011]
Machine Learning [S&P 2013]
Personalized Medicine,
Medical Research
[USENIX Sec 2011]
Private Set Intersection
[NDSS 2012]
Obliv-C](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-21-2048.jpg)

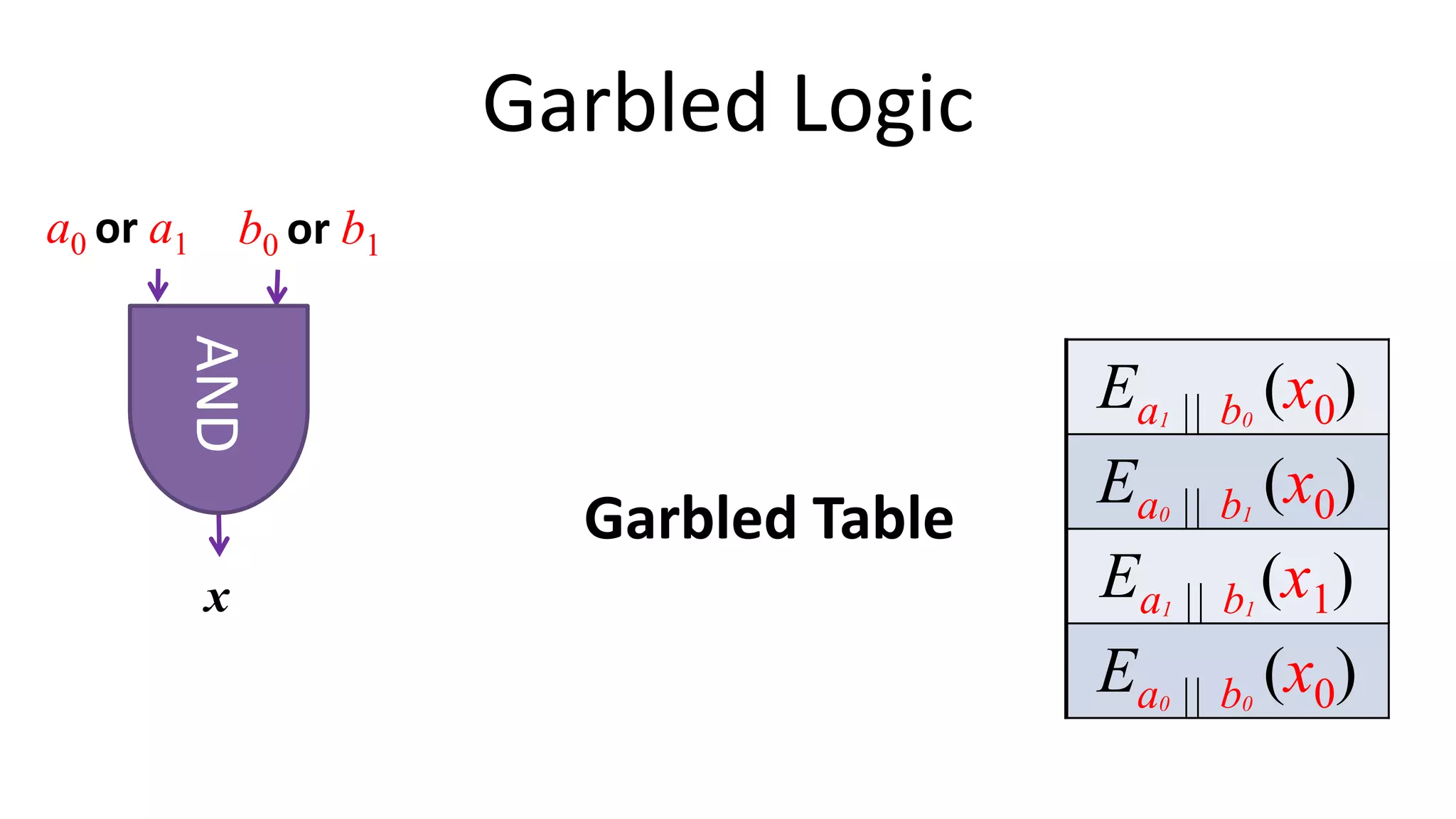
![Background: Point-and-Permute
Enca0,,b0,
(c0)
Enca0,,b1
(c0)
Enca0,,b0
(c0)
Enca1,b1
(c1)
Encoding garble table entries:
Input wire labels
(with selection bits)
Output wire label
Beaver, Micali and Rogaway [STOC 1990]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-24-2048.jpg)
![Background: Garbled Row Reduction
Naor, Pinkas and Sumner [1999]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-25-2048.jpg)
![Background: Garbled Row Reduction
Naor, Pinkas and Sumner [1999]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-26-2048.jpg)
![Background: Garbled Row Reduction
Naor, Pinkas and Sumner [1999]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-27-2048.jpg)
![Background: Free-XOR
Kolesnikov and Schneider [2008]
Global
generator
secret](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-28-2048.jpg)
![Background: Free-XOR
Kolesnikov and Schneider [2008]
Global
generator
secret](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-29-2048.jpg)
![Background: Free-XOR
Kolesnikov and Schneider [2008]
Global
generator
secret
XOR are free! No ciphertexts or encryption needed.](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-30-2048.jpg)
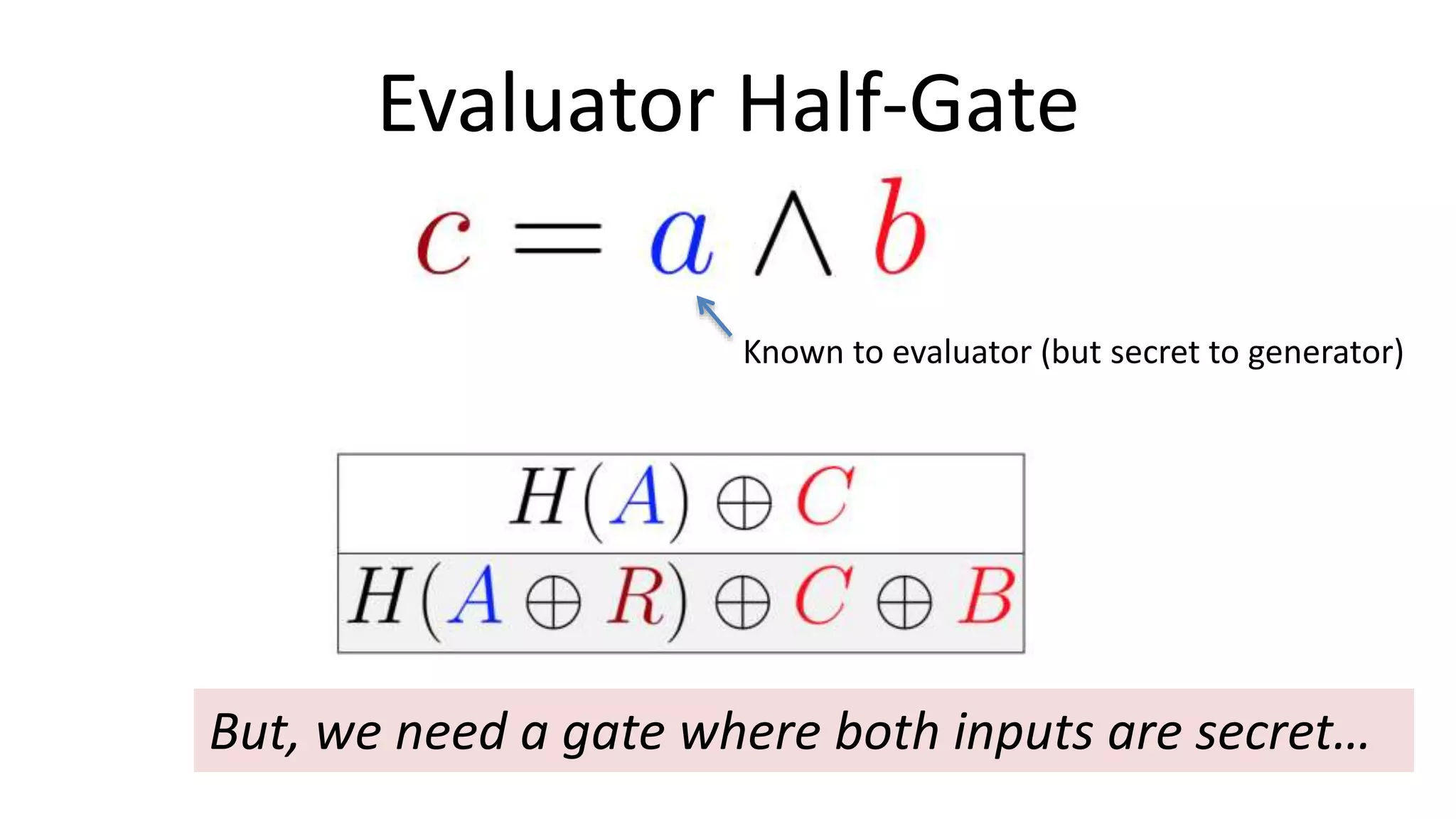
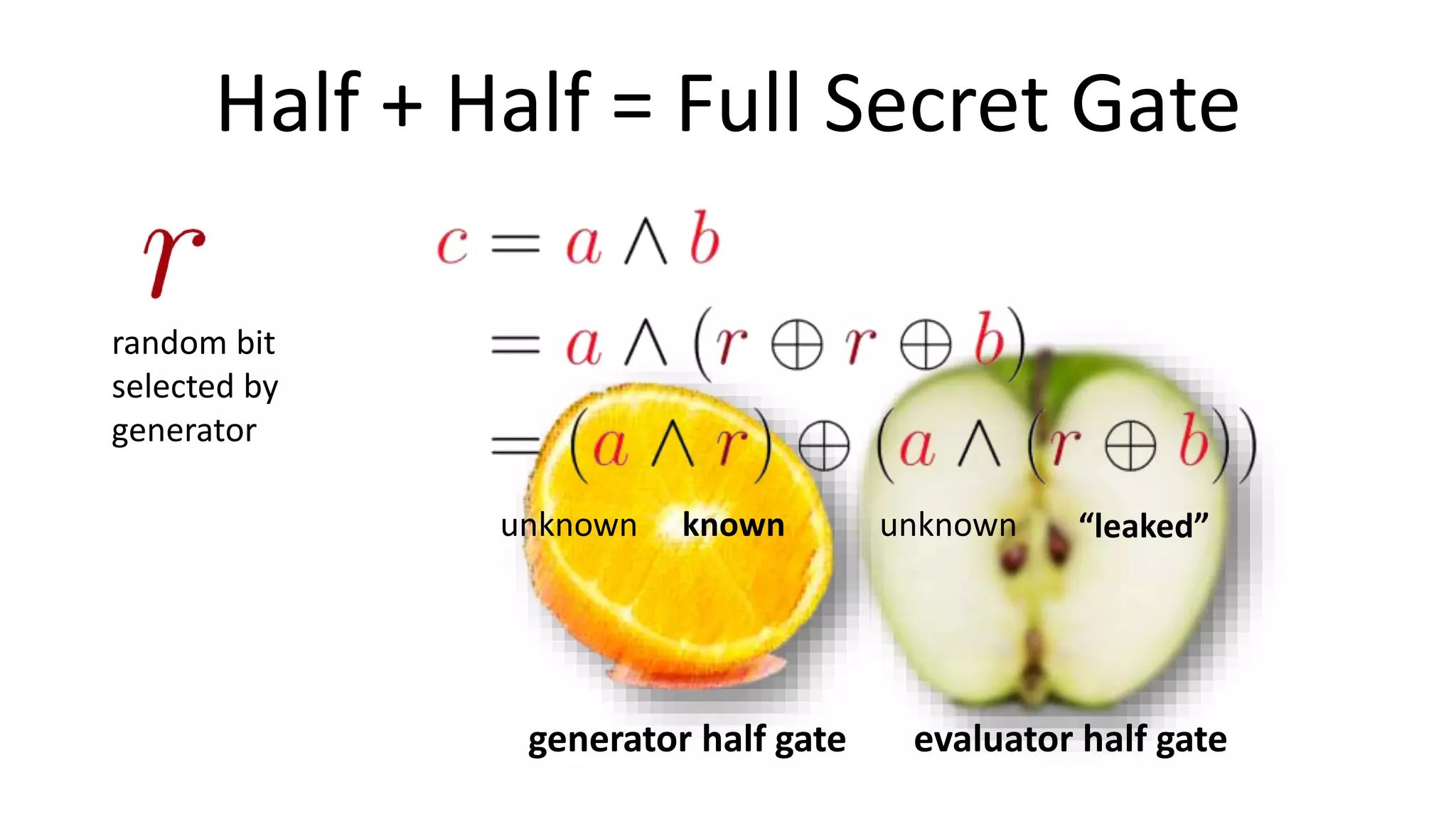
![Half Gates
Yan Huang, David Evans, and Jonathan Katz.
Private Set Intersection: Are Garbled Circuits
Better than Custom Protocols? [NDSS 2012]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-31-2048.jpg)
![Yan Huang, David Evans, and Jonathan Katz.
Private Set Intersection: Are Garbled Circuits
Better than Custom Protocols? [NDSS 2012]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-32-2048.jpg)
![Yan Huang, David Evans, and Jonathan Katz.
Private Set Intersection: Are Garbled Circuits
Better than Custom Protocols? [NDSS 2012]
Journal of the ACM, January 1968
swap gates, configured (by generator)
to do random permutation](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-33-2048.jpg)





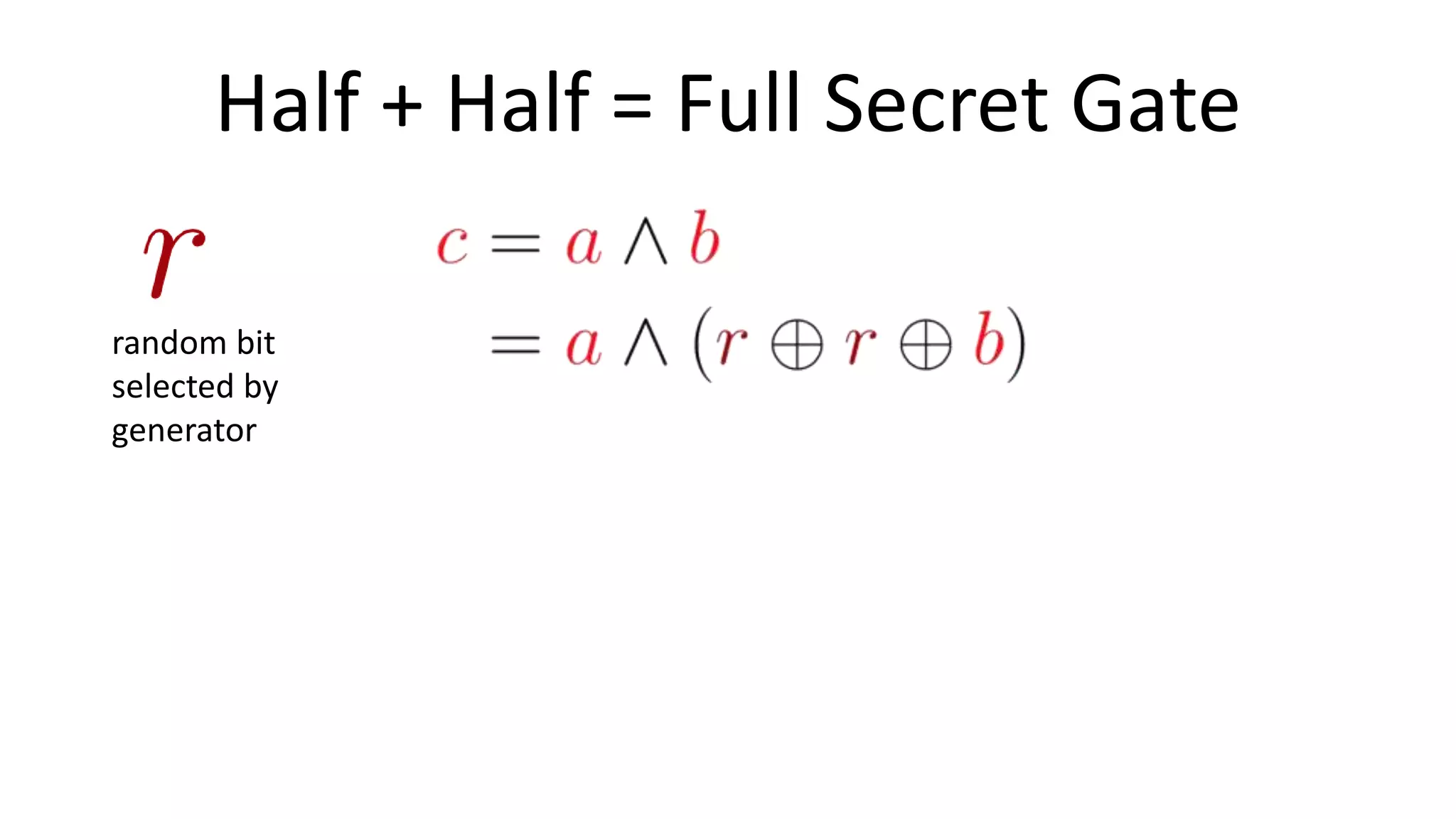





![for (i = 1; i <= n1; ++i) {
for(j = 1; j <= n2; ++j) {
Accum temp = acMin (dp[i][j-1], dp[i-1][j]);
obliv bool d = true;
obliv if (acLessEq(dp[i-1][j-1], temp)) {
acCopy(&temp, &dp[i-1][j-1]);
d = (s1[i-1] != s2[j-1]);
}
ScalingMPC
Gate Execution
Protocols
Ea0,1||b0,0
(x0,0)
Ea0,0||b0,1
(x0,0)
Ea0,1||b0,1
(x0,1)
Ea0,0,|b0,1
(x0,0)
Circuit Construction
Private Biometrics
[NDSS 2011]
Machine Learning [S&P 2013]
Personalized Medicine,
Medical Research
[USENIX Sec 2011]
Private Set Intersection
[NDSS 2012]
obliv-C](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-47-2048.jpg)
![Fairplay
48
Malkhi, Nisan, Pinkas and
Sella [USENIX Sec 2004]
SFDL Program
SFDL
Compiler
Circuit
(SHDL)
Alice Bob
Garbled Tables
Generator
Garbled Tables
Evaluator
SFDL
Compiler](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-48-2048.jpg)




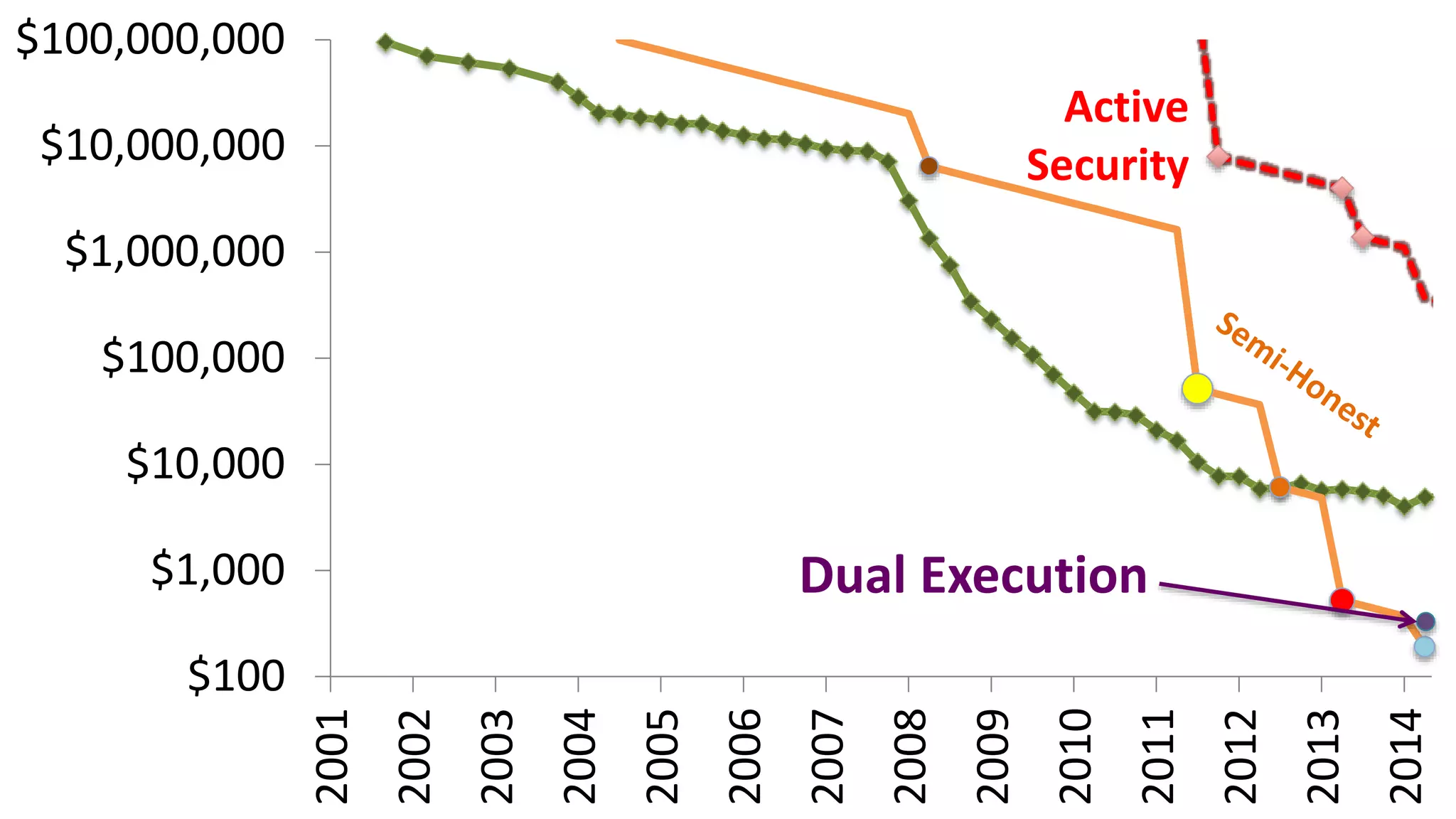
![$100
$1,000
$10,000
$100,000
$1,000,000
$10,000,000
$100,000,000
2001
2002
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
Semi-Honest
Active
Security
Symmetric
Cut-and-Choose
[HKE 2013]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-53-2048.jpg)

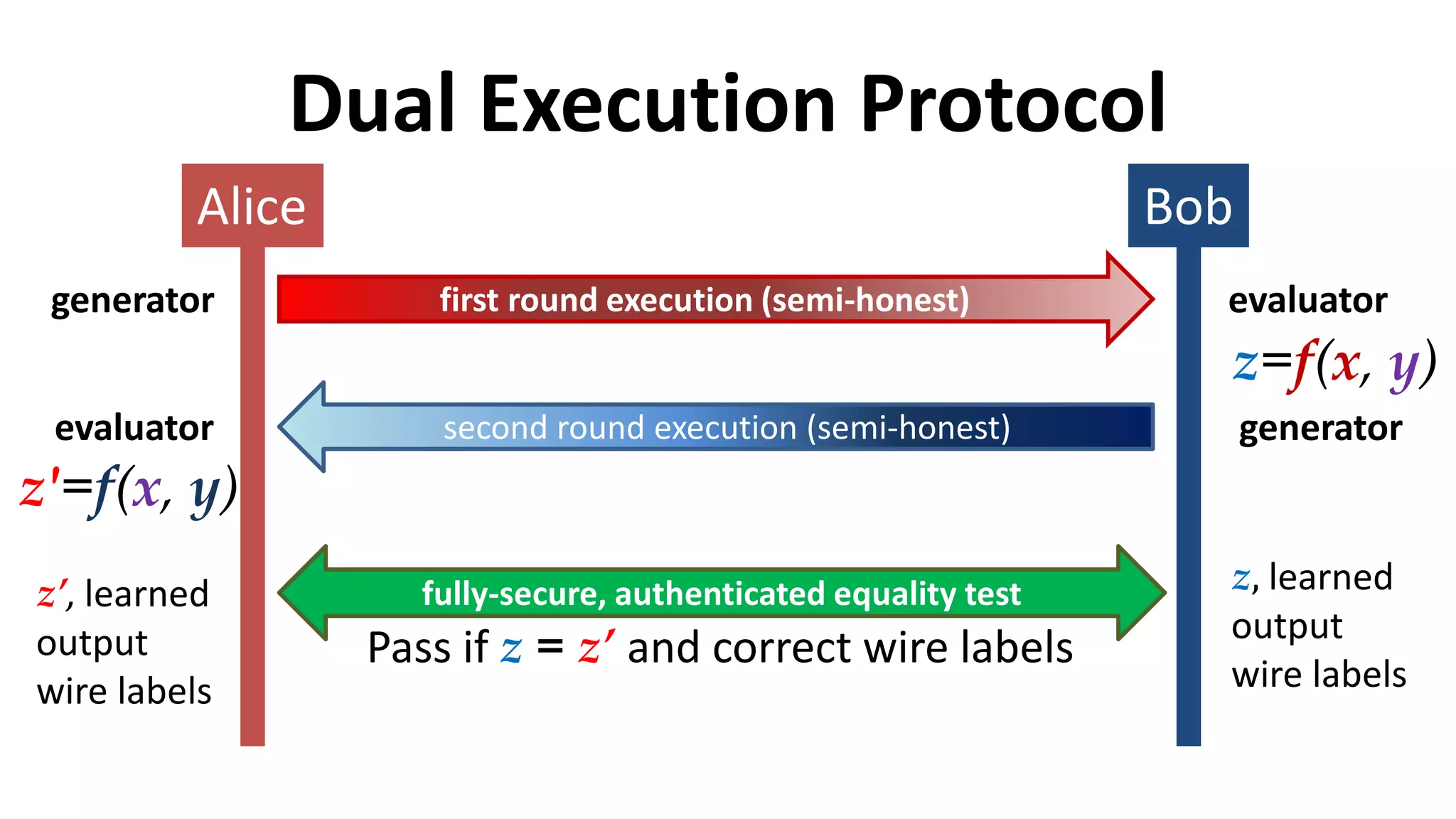
![Dual Execution Protocols
Yan Huang, Jonathan Katz, David Evans.
[IEEE S&P (Oakland) 2012]
Mohassel and Franklin. [PKC 2006]](https://image.slidesharecdn.com/darmstadt-150604164201-lva1-app6891/75/Multi-Party-Computation-for-the-Masses-55-2048.jpg)