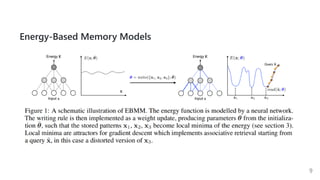
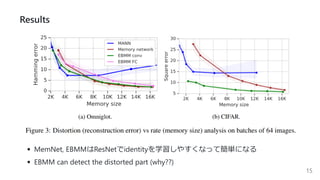
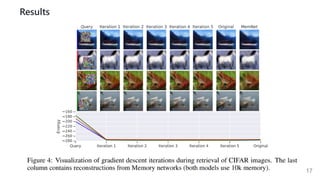
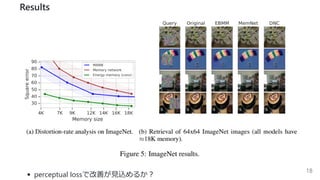
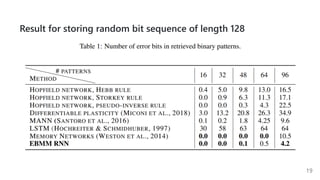
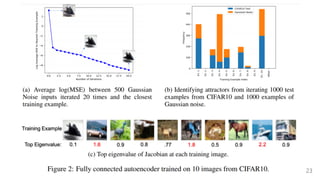
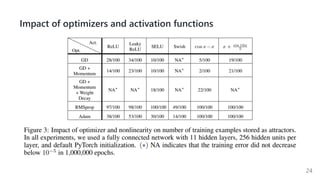
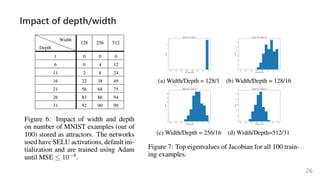
This document summarizes several papers on associative memory models. It discusses Hopfield networks, energy-based deep learning models, and how overparameterized neural networks can implement associative memory through their dynamics. Key points include: Hopfield networks use binary neurons and symmetric weights to retrieve stored patterns via network dynamics; energy-based models aim to store patterns as local minima and retrieve them through energy minimization; overparameterized autoencoders can exhibit associative memory properties without explicit energy functions through their iterative dynamics.

1. Associative Memory Model について
2020/10/04
1

2. Referrence
1. The Capacity of Hopfield Associated Memory (1987)
2. Meta Learning Deep Energy-Based Memory Models (ICLR 2020)
3. Overparameterized Neural Networks Implement Associated Memory (2019)
4. 関連︓Identity Crisis: Memorization and Generalization under Extreme
Overparameterization (ICLR 2020)
5. 後で読みたい︓Associative Memory in Iterated Overparameterized Sigmoid
Autoencoders (ICML2020)
2

3. Mathmatical Preliminaries
Dynamical systems on state space
behavior of a state with transition given by
Fixed points
state such that
Attractors (≒ stable fixed points)
A fixed point is (locally) stable if any states near converge by
successively applying .
(本当は集合に対して定める, e.g. limit cycle)
Theorem
For differentiable , a fixed point of is stable Jacobian of at has
maximum (absolute) eigenvalue less than 1.
V (= R , {0, 1} , manifolds, etc.)n n
x ∈ V x ← F(x) F : V → V
x x = F(x)
x x x
F
F x F ⟺ F x
3

4. Associative Memory Model
Model to retrieve remembered patterns from distorted/incomplete version
STORE patterns as attractors of network dynamics
RETRIEVE by running dynamics
Retrieval often written as optimization procedure of Energy function
Hopfield network
(Deep) Boltzman machine
Energy based deep network (Referrence 2)
(モチベーションがよくわからないという話はある)
4

5. Hopfield Network
Hopfield Network consists of
Binary neurons (state vector)
Symmetric matrix (parameter)
State transition (dynamics)
x ∈ {0, 1}n
T ∈ Rn×n
x ←i sgn(Tx) =i sgn( T x )∑j ij j
sgn(0) := +1
5

6. Hopfield Network for Memory Model
: vectors to be stored ( should be small )
Encoding rule
Retrieval
Hopfield's Asynchronous Algorithm
a. take an initial state
b. choose randomly
c.
d. repeat 2,3
returns
{x , ⋯ , x } ⊂(1) (m)
{+1, −1}n
m < n
T = (x x −∑α=1
m (α) (α)T
I )n
i ∈ {1, ⋯ , n}
x ←i sgn(Tx)i
x
6

7. Hopfield Network for Memory Model
The algorithm converges, but limits are NOT necessarily s
For small , s tend to be stable attractors (w.r.t. Hamming distance)
Energy of Hopfield Network
Theorem (Hopfield)
: symmetric, diagonal , then the energy does not increase by state
transition, and asynchronous algorithm converges.
x(α)
m < n x(α)
E := − T x x∑i,j ij i j
T ≥ 0 E
7

8. Meta-Learning Deep Energy-Based Memory Models
S. Batrunov, J. W. Rae, S. Osindero, T. P. Lillicrap (Google Brain)
Construct memory models for more complex data (e.g. images)
Represent higher order dependency in real-world data
Need compressive (≒expressive) & fast writing rule with energy
Use deep networks
Apply gradient-based meta-learning methods (Finn et al., 2017)
8

9. Energy-Based Memory Models
9

10. Energy-Based Memory Models
Parametric model differentiable in both
Aims to compress patterns into parameters so that each
becomes a local minimum of
Retrieve from distorted by calling (energy-minimization)
Practically quantified by reconstruction error:
(expection taken over distortion ?)
E(x; θ) x, θ
X = {x , ⋯ , x }1 N θ
xi E(x; θ)
xi x~i read( ; θ)x~i
x ↦ x~
10

11. Meta-Learning Gradient-Based Writing Rules
Naive EBMM requires many iterations for to converge (i.e. writing is slow)...
Want to find good initial parameter for fast optimization
Hard to evaluate and differentiate expectation over distortion...
Introduce writing loss
Including only 1st-order information (w/o Hessian) is empirically sufficient
Limits deviation from initial is empirically helpful
Define (explicit) writing rule
(continued...)
θ
θˉ
θˉ
write
11

12. Meta-Learning Gradient-Based Writing Rules
Hard to evaluate and differentiate expectation over distortion...
(...continued)
meta-learn by
where
(remark : need access to whole dataset, not only one set to store)
Use (number of iteration for write/read) in the experiment
r = ({γ }, {η }), τ =(k) (t)
(α, β)
X
K = T = 5
12

13. Experiments : Retrieval for real-world image
Baseline
LSTM (failed)
Hopfield networks (failed)
Memory-Augmented Networks (Santoro et al., 2016)
Memory Networks (Wetson et al., 2014)
Differentiable Plasticity model (Miconi et al., 2018)
Dynamic Kanerva Machine (Wu et al., 2018)
Datasets
Omniglot characters
CIFAR-10
ImageNet 64x64 13

14. Experiments : Retrieval for real-world image
Procedure (varying memory size)
Write a fixed-sized batch of images
Form queries by corrupting a random block of the images
Retrieve the original image.
Use FC (only for Omniglot) or Conv in 3-block ResNet for proposed model.
Energy is computed as a linear combination of units in the last layer.
14

15. Results
MemNet, EBMMはResNetでidentityを学習しやすくなって簡単になる
EBMM can detect the distorted part (why??)
15

16. Results
16

17. Results
17

18. Results
perceptual lossで改善が⾒込めるか︖
18

19. Result for storing random bit sequence of length 128
19

20. Overparameterized Neural Networks Implement
Associative Memory
A.Radhakrishnan (MIT), M.Belkin (Ohio State Univ.), C.Uhler (MIT)
Empirically show:
Overparameterized autoencoders has associated memory as attractors (w/o
explicit energy!)
Efficient sequence encoding with the same mechanism
ICLR 2020 reject
Not convincing for applicability to classifier or more general models
⾯⽩いが、インパクトや⽴ち位置が不⼗分。もうちょっと結果が欲しい
20

21. Dynamics defined by autoencoder
Autoencoder can be iterated
Hence define a dynamical system on the data space.
Sequence encoder can be trained by modifying the MSE loss:
L = ∣∣f(x ) −(i)
x ∣∣(i+1 mod n) 2
Sequential counterpart of stable fixed points are called a limit cycle
In this paper, the authors analyze
the dynamics defined by AEs trained to achieve MSE
varying activation / optimizer / initialization / depth and width
Remark : Reference 4 analyzes AEs with 1 training datum focusing on architectures,
but not on dynamics.
f : R →d
Rd
< 10−8
21

22. Retrieval via iteration
Spurious (i.e. out of stored data) attractors sometimes appear (depending on
dataset & optimization).
22

23. 23

24. Impact of optimizers and activation functions
24

25. Analysis for Convolutional Networks
25

26. Impact of depth/width
26

27. Efficiency of Sequence Encoder
27