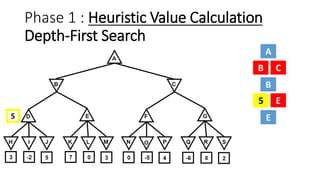
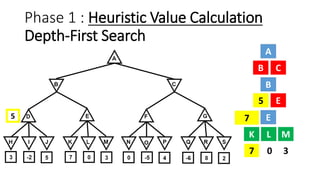
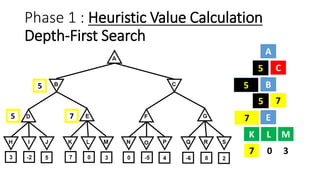
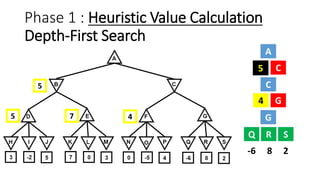
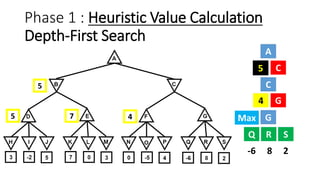
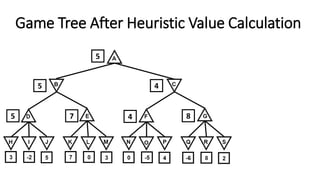
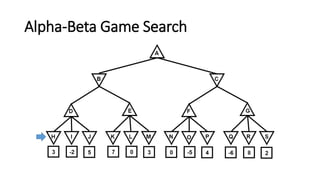
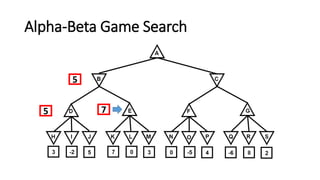
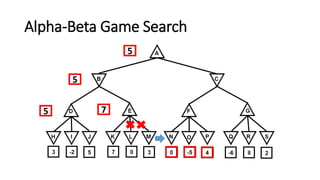
The document discusses the minimax game search algorithm used in artificial intelligence, explaining how two players (max and min) take turns to optimize their scores. It details the process of finding heuristic values for nodes, the steps involved in the search, and introduces alpha-beta pruning as a more efficient modification that avoids exploring less useful nodes. The text concludes by highlighting that if both players play optimally, max will win with a specific score, emphasizing the benefits of using alpha-beta pruning over traditional minimax.

1. AI Game Search
MENOUFIA UNIVERSITY
FACULTY OF COMPUTERS AND INFORMATION
ALL DEPARTMENTS
ARTIFICIAL INTELLIGENCE
‫المنوفية‬ ‫جامعة‬
‫والمعلومات‬ ‫الحاسبات‬ ‫كلية‬
‫األقسام‬ ‫جميع‬
‫الذكاء‬‫اإلصطناعي‬
‫المنوفية‬ ‫جامعة‬
Ahmed Fawzy Gad
ahmed.fawzy@ci.menofia.edu.eg

2. Minimax

3. Minimax Game Search

4. Minimax Game Search
Two Players take turns:
Max and Min

5. Minimax Game Search
Two Players take turns:
Max and Min
Max : Maximizes Score.
Min : Minimizes Score.
MAX

6. Minimax Game Search
Two Players take turns:
Max and MinMAX
MIN

7. Minimax Game Search
Two Players take turns:
Max and Min
Max : Maximizes Score.
Min : Minimizes Score.
MAX
MIN

8. Minimax Game Search
Two Players take turns:
Max and Min
Max : Maximizes Score.
Min : Minimizes Score.
Special Case.
Max is an expert.
Min is a beginner.
MAX
MIN

9. Minimax Game Search
A

10. Minimax Game Search
Which node to follow?
No heuristic values.
A
B C

11. Minimax Game Search
Which node to follow?
No heuristic values.
A
B C

12. Minimax Game Search
Which node to follow?
No heuristic values.
A
B C
Hot to find heuristic values
for other nodes?

13. Minimax Game Search
Which node to follow?
No heuristic values.
A
B C
Hot to find heuristic values
for other nodes?
Use children heuristics to
calculate parent heuristic.

14. Minimax Game Search
Which node to follow?
No heuristic values.
A
B C
Hot to find heuristic values
for other nodes?
Use children heuristics to
calculate parent heuristic.
Minimax Game
Search Steps

15. Minimax Game Search
Which node to follow?
No heuristic values.
A
B C
Hot to find heuristic values
for other nodes?
Use children heuristics to
calculate parent heuristic.
Minimax Game
Search Steps
Calculate
Heuristics

16. Minimax Game Search
Which node to follow?
No heuristic values.
A
B C
Hot to find heuristic values
for other nodes?
Use children heuristics to
calculate parent heuristic.
Minimax Game
Search Steps
Calculate
Heuristics
Search

17. Phase 1 : Heuristic Value Calculation
Depth-First Search
A

18. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B

19. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B C

20. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B CB C

21. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
C

22. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
C
D E
B C

23. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
C
D E
B C
D E

24. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
C
D E
B C
D E

25. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
B C
D E

26. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
B C
D E
H I J

27. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
B C
D E
H I J

28. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
3 -2 5
B C
D E
H I J

29. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
3 -2 5
B C
D E
H I J
Max

30. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
3 -2 5
B C
D E
H I J
Max
5

31. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
3 -2 5
B C
D E
H I J
Max
5
5

32. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
3 -2 5
B C
D E
H I J
Max
5
5
5

33. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
D
H I
C
D E
J
3 -2 5
B C
D E
H I J
Max
5
5
5
5

34. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
C
D E
B C
D E5
5

35. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
C
D E
B C
D E5
5

36. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
B C
D E5
5

37. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
B C
D E
K L M
5
5

38. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
5
5

39. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
5
5

40. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
7
5
5

41. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
7
7
5
5

42. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
7
7
75
5

43. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
7
7
7
Min
5
75

44. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
7
7
7
Min5
55
75

45. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
7
7
7
Min5
5
55
75

46. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
B
E
K L
C
D E
M
7 0 3
B C
D E
K L M
Max
7
7
7
Min5
5
55
7
5
5

47. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B CB C5
7
5
5

48. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
CB C5
7
5
5

49. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
C
F G
B C5
7
5
5

50. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
C
F G
B C5
F G
7
5
5

51. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
C
F G
B C5
F G
7
5
5

52. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
B C5
F G
7
5
5

53. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
B C
N O P
5
F G
7
5
5

54. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
0 -5 4
B C
N O P
5
F G
7
5
5

55. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
0 -5 4
B C
N O P
Max
5
F G
7
5
5

56. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
0 -5 4
B C
N O P
Max
4
5
F G
7
5
5

57. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
0 -5 4
B C
N O P
Max
4
5
4
F G
7
5
5

58. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
0 -5 4
B C
N O P
Max
4
5
4
F G4
7
5
5

59. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
F
N O
C
F G
P
0 -5 4
B C
N O P
Max
4
5
4
F G4
47
5
5

60. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
C
F G
B C5
F G4
47
5
5

61. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
C
F G
B C5
F G4
47
5
5

62. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
B C5
F G4
47
5
5

63. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
B C
Q R S
5
F G4
47
5
5

64. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
5
F G4
47
5
5

65. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
5
F G4
47
5
5

66. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
F G4
47
5
5

67. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4
47
5
5

68. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
47
5
5

69. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min
847
5
5

70. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min4
4
847
5
5

71. Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min4
4
4
847
5
5
4

72. Max
Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min4
4
4
847
5
5
4

73. Max
Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min4
4
4
5
8
4
47
5
5

74. Max
Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min4
4
4
5
5
8
4
47
5
5

75. Max
Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min4
4
4
5
5
8
4
5
47
5
5

76. Max
Phase 1 : Heuristic Value Calculation
Depth-First Search
A
B
C
G
Q R
C
F G
S
-6 8 2
B C
Q R S
Max
8
5
8
F G4 8
Min4
4
4
5
5
8
4
5
47
5
5
If both players play optimally then Max will win by a score 5.

77. Game Tree After Heuristic Value Calculation
8
4
5
47
5
5

78. Phase 2 : Game Search
8
4
5
47
5
5

79. Phase 2 : Game Search
8
4
5
47
5
5
A

80. Phase 2 : Game Search
8
4
5
47
5
5
BMax
A

81. Phase 2 : Game Search
8
4
5
47
5
5
B
D
Max
A
Min

82. Phase 2 : Game Search
8
4
5
47
5
5
B
D
J
Max
Min
Max
A

83. Minimax Game Search Drawback
• Expands all the tree
while not all
expanded nodes are
useful.

84. Minimax Game Search Drawback
• Expands all the tree
while not all
expanded nodes are
useful.
• In this example, just
few nodes of the
whole tree was useful
in reaching the goal.

85. Alpha-Beta Pruning

86. Alpha-Beta Pruning = Minimax Except
• This game search strategy is a modification to Minimax game search
that avoids exploring nodes that are not useful in the search.
• It gives the same results as Minimax but avoids exploring some
nodes.
• In the previous example, the path explored using Minimax was A-B-D-
J.
• Also the Alpha-Beta Pruning path will be A-B-D-J but without
exploring all nodes as in Minimax.

87. Alpha-Beta Pruning Motivation
Never explore values that are not useful.
=Min(Max(1, 2, 5), Max(6, x, y), Max(1, 3, 4))
=Min(5, Max(6, x, y), 4)
=Min(Max(6, x, y), 4)
=4

88. Alpha-Beta Game Search

89. Alpha-Beta Game Search

90. Alpha-Beta Game Search

91. Alpha-Beta Game Search

92. Alpha-Beta Game Search

93. Alpha-Beta Game Search
5

94. Alpha-Beta Game Search
5
5

95. Alpha-Beta Game Search
5
5

96. Alpha-Beta Game Search
5
5

97. Alpha-Beta Game Search
5
5

98. Alpha-Beta Game Search
7
5
5

99. Alpha-Beta Game Search
7
5
5
Min(5, max(7, x, y))
=5

100. Alpha-Beta Game Search
7
5
5

101. Alpha-Beta Game Search
7
5
5

102. Alpha-Beta Game Search
7
5
5

103. Alpha-Beta Game Search
7
5
5
5

104. Alpha-Beta Game Search
7
5
5
5

105. Alpha-Beta Game Search
7
5
5
5

106. Alpha-Beta Game Search
7
5
5
5

107. Alpha-Beta Game Search
7
5
5
5

108. Alpha-Beta Game Search
7
5
5
5
4

109. Alpha-Beta Game Search
7
5
5
5
4
4
Max(5, min(4, x, y, z))
=5

110. Alpha-Beta Game Search
7
5
5
5
4
4

111. Alpha-Beta Game Search
7
5
5
5
4
4

112. Alpha-Beta Game Search
7
5
5
5
4
4
Same results as Minimax
with fewer nodes explored.
5 Unexplored Branches.