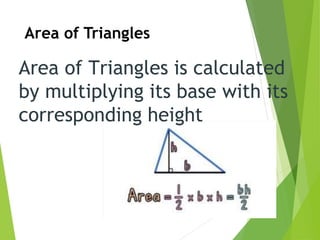
This digital plan outlines a 45-minute lesson on calculating the areas of parallelograms and triangles for a 9th grade mathematics class. It will cover defining and properties of parallelograms and triangles, their area formulas, and theorems related to congruency. The lesson aims to develop students' problem solving, reasoning, communication, making connections to real-life, and visualization/representation skills through exploring these geometric shapes and their areas.

1. Digital Plan - 4
Preliminary Information
Name: BSD
Roll No.: 1642-
Subject: Mathematics
Class: IX
Topic: Areas
Duration: 45 min
Method: Digital Plan

2. Academic Standards
1. Problem Solving – Student will be able to solve problems
based on areas of parallelogram and triangle
2. Reasoning Proof – Students will be able to ask for reasoning
and proof of how the area is calculated for parallelograms and
triangles
3. Communication – Students will be able to communicate the
definitions of a parallelogram, triangle and congruency
4. Connection – Student will be able to connect the area
formulae to the real-life objects
5. Visualization and Representation – Student will be able to
visualize the different parallelograms and triangles, and
represent them accordingly

3. AREAS OF
PARALLELOGRAMS AND
TRIANGLES

4. Content Analysis
 Definition of a Parallelogram
 Properties of a Parallelogram
 Area of Parallelogram
 Definition of a Triangle
 Properties of a Triangle
 Area of Triangle
 Congruency
 Theorems related to Congruency

5. PARALLELOGRAM
 A quadrilateral is called a parallelogram, if
both pairs of its opposite sides are parallel.
In the adjoining figure, ABCD is a
quadrilateral in which
AB ∥ DC and AD ∥ BC.
So, ABCD is a parallelogram.
PROPERTIES OF PARALLELOGRAM.
 Opposite sides are parallel and congruent.
 Opposite angles are congruent.
 Consecutive angles are supplementary.
 The diagonals bisect each other.

6. Area of Parallelograms
Area of Parallelograms is
calculated by multiplying
its base to its
corresponding height

7. TRIANGLE
A triangle is a polygon with three edges and
three vertices. It is one of the
basic shapes in geometry. A triangle with
vertices A, B, and C is denoted ABC.

8. Area of Triangles
Area of Triangles is calculated
by multiplying its base with its
corresponding height

9. •The part of the plane enclosed by a simple closed
figure is called a planar region corresponding to that
figure. The magnitude or measure of this planar region
is called its area. This magnitude or measure is always
expressed with the help of a number (in some unit)
such as 5 cm2 ,8m2 ,3 hectares , etc. so, we can say
that area of a figure is a number (in some unit)
associated with the part of the plane enclosed by the
figure with the following two properties:
•(1) If A and B are two congruent figures, then ar(A) =
ar(B)
•(2) If a planar region formed by a figure T is made up
of two non-overlapping planar regions formed by
figures P and Q, then ar(T)= ar(P) + ar(Q)

10. In geometry, two figures or objects
are congruent if they have the
same shape and size, or if one has the same
shape and size as the mirror image of the
other.
•If two figures A and B are congruent, they
must have equal areas. However, the
converse of this statement is not true.
•Two figures having equal areas need not be
congruent.
COGRUENCY

13. Figures on the Same Base and Between
the Same Parallels