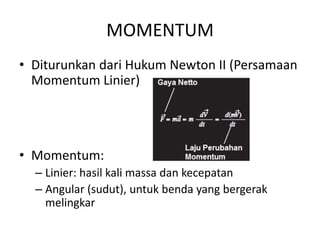
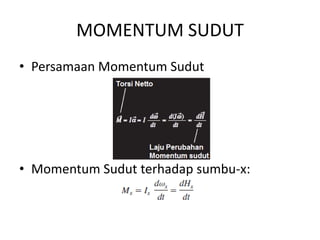
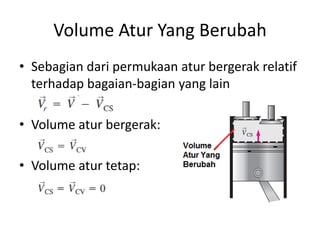
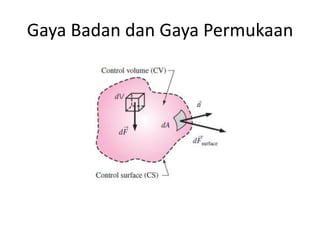
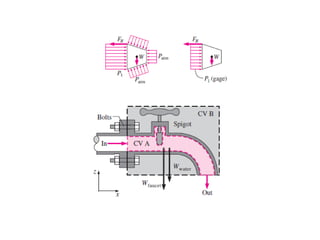
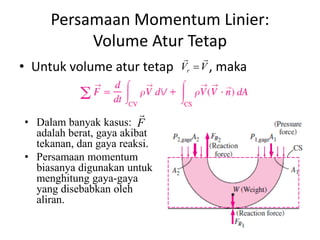
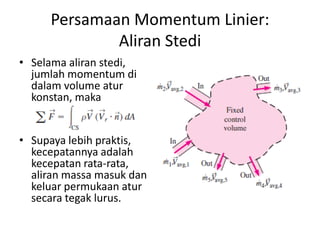
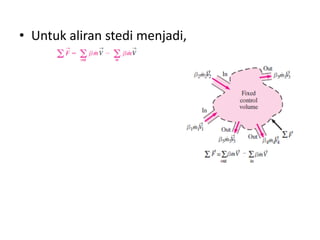
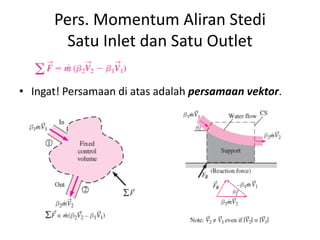
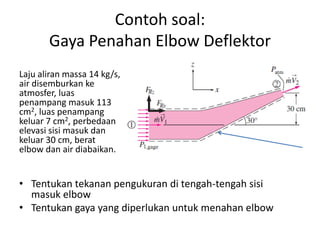
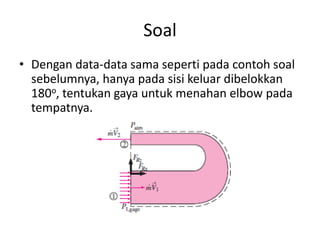
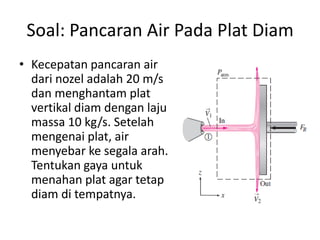
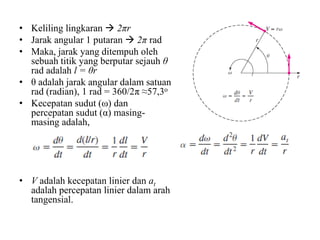
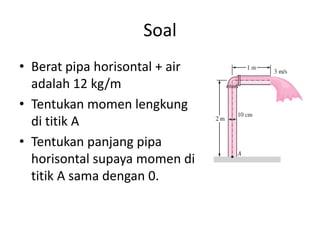
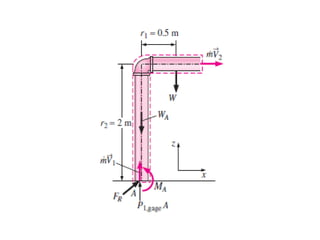
Analisis momentum aliran fluida membahas prinsip kekekalan momentum linier dan sudut serta penerapannya untuk menganalisis gaya pada sistem fluida dalam keadaan diam atau bergerak, seperti elbow, roket, atau pipa horisontal. Persamaan momentum digunakan untuk menghitung gaya-gaya seperti gaya dorong, penahan, atau lengkung pada berbagai kondisi aliran.

1. ANALISIS MOMENTUM ALIRAN FLUIDA

2. MOMENTUM
• Diturunkan dari Hukum Newton II (Persamaan
Momentum Linier)
• Momentum:
– Linier: hasil kali massa dan kecepatan
– Angular (sudut), untuk benda yang bergerak
melingkar

3. PRINSIP KEKEKALAN MOMENTUM
• Momentum suatu sistem konstan bila tidak
ada gaya yang bekerja pada sistem.
• Prinsip ini berguna untuk menganalisis
tumbukan dan ledakan.

4. Contoh Soal
• Sebuah bus yang massanya 2000 kg bergerak dengan kecepatan 50
km/jam. Hitung momentumnya!
 100000 kg km/jam
km  1000m  1 jam 
1000
 100000.
kg.m / s



jam  1km  3600s 
3600
• Kalau bus itu melakukan pengereman sehingga kecepatannya turun
menjadi 10 km/jam dalam waktu 1 menit, berapa gaya
pengeremannya? 50 km / jam  10 km / jam
km / jam
 100000 kg
– Perlambatan=
 40
1menit
menit
 1000 m / 3600 s 
40000

 40 
m / s2

 3600 X 60
60 s


– Gaya perlambatan= 2000 kg X perlambatan

5. MOMENTUM SUDUT
• Persamaan Momentum Sudut
• Momentum Sudut terhadap sumbu-x:

6. MEMILIH VOLUME ATUR
• Volume Atur:
– Tetap
– Bergerak
– Berubah bentuk
• Laju aliran yang masuk ke dan keluar dari
volume atur tergantung dari kecepatan aliran
relatif terhadap permukaan atur.

7. Volume Atur Tetap

8. Volume Atur Yang Bergerak

9. Volume Atur Yang Berubah
• Sebagian dari permukaan atur bergerak relatif
terhadap bagaian-bagian yang lain
• Volume atur bergerak:
• Volume atur tetap:

10. GAYA-GAYA PADA VOLUME ATUR
• Gaya-gaya Badan: gaya-gaya yang bekerja pada
benda secara keseluruhan,
– gaya listrik
– gaya gravitasi
– gaya magnetik
• Gaya-gaya Permukaan: gaya-gaya yang bekerja
pada permukaan atur,
– tekanan
– gaya viskositas
– gaya reaksi pada titik kontak

11. Gaya Badan dan Gaya Permukaan

12. Gaya Badan
• Gaya gravitasi pada
elemen fluida:
• Dengan mengabaikan
gaya listrik dan
magnet, gaya badan
total:

13. Gaya Permukaan
• Arah sumbu koordinat diputar sesuai kebutuhan

14. Gaya Permukaan
• Gaya total permukaan yang bekerja pada
permukaan atur

15. Gaya Total Pada Volume Atur

17. PERSAMAAN MOMENTUM LINIER
• Dari
• Karena massa jenis fluida bisa jadi berubah maka
persamaan di atas bisa juga ditulis menjadi:
• Dari persamaan di atas, hukum Newton II dapat dinyatakan
dengan: jumlah semua gaya-gaya eksternal yang bekerja
pada sistem sama dengan laju perubahan momentum linier
sistem.
• Pernyataan di atas valid untuk sistem koordinat dalam
keadaan diam atau bergerak dengan kecepatan konstan,
yang disebut sistem koordinat inersia.

18. • Menggunakan Teorema Transport Reynolds formulasi
sistem dapat diubah ke formulasi volume atur
• Dengan menetapkan
maka

19. • Ruas kiri dari persamaan terakhir di atas
adalah
, maka:
• Yang dapat dinyatakan dengan:
 jumlah semua gaya 
  laju perubahan   laju aliran momentum linier


 
 

 gaya eksternal yang
   momentum linier    netto yang masuk dan keluar dari 
 bekerja pada volume atur   isi volume atur   permukaan atur oleh aliran massa 

 
 

• Di sini
, yaitu kecepatan fluida
relatif terhadap permukaan atur.

• V adalah kecepatan fluida terhadap sistem
koordinat inersia

20. Persamaan Momentum Linier:
Volume Atur Tetap
• Untuk volume atur tetap

• Dalam banyak kasus: F
adalah berat, gaya akibat
tekanan, dan gaya reaksi.
• Persamaan momentum
biasanya digunakan untuk
menghitung gaya-gaya
yang disebabkan oleh
aliran.
 
Vr  V ,
maka

21. Persamaan Momentum Linier:
Aliran Stedi
• Selama aliran stedi,
jumlah momentum di
dalam volume atur
konstan, maka
• Supaya lebih praktis,
kecepatannya adalah
kecepatan rata-rata,
aliran massa masuk dan
keluar permukaan atur
secara tegak lurus.

22. • Laju aliran massa masuk dan keluar dengan
massa jenis (hampir) konstan,
• Dan laju momentum masuk dan keluar
menjadi

23. Faktor Koreksi Fluks Momentum, β
• Karena kenyataannya kecepatan masuk dan
keluar tidak seragam, maka persamaan
momentum harus dikoreksi dengan β, menjadi
• Untuk aliran laminar, β = 4/3
• Untuk aliran turbulen, β antara 1,01 s.d. 1,04

24. • Untuk aliran stedi menjadi,

25. Pers. Momentum Aliran Stedi
Satu Inlet dan Satu Outlet
• Ingat! Persamaan di atas adalah persamaan vektor.

26. Persamaan Momentum Sepanjang
Sumbu Koordinat
• Pada sumbu-x,
• Untuk aliran tanpa gaya-gaya eksternal,
• “laju perubahan momentum di dalam volume
atur adalah selisih laju aliran momentum yang
masuk dan keluar”

27. • Jika massa yang masuk dan keluar hampir
konstan,
• Volume atur di sini bisa dianggap sebagai
benda tegar dengan gaya netto (thrust),

28. Contoh: Gaya Dorong Roket
• Gaya dorong roket
dihasilkan oleh
perubahan
momentum oleh
bahan bakar yang
dipercepat dari nol ke
kecepatan keluar
sekitar 2000 m/s
akibat pembakaran.

29. Contoh soal:
Gaya Penahan Elbow Deflektor
Laju aliran massa 14 kg/s,
air disemburkan ke
atmosfer, luas
penampang masuk 113
cm2, luas penampang
keluar 7 cm2, perbedaan
elevasi sisi masuk dan
keluar 30 cm, berat
elbow dan air diabaikan.
• Tentukan tekanan pengukuran di tengah-tengah sisi
masuk elbow
• Tentukan gaya yang diperlukan untuk menahan elbow

30. Asumsi:
1. Alirannya stedi, gesekan diabaikan
2. Berat elbow dan air diabaikan
3. Air keluar dari elbow pada tekanan atmosfer,
sehingga tekanan pengukurannya nol
4. Alirannya turbulen, dan β = 1,03




m1  m2  m  14 kg / s dan m  AV , maka:

31. • Tekanan di sisi masuk dihitung menggunakan
persamaan Bernoulli
• Persamaan momentum aliran stedi:

33. Soal
• Dengan data-data sama seperti pada contoh soal
sebelumnya, hanya pada sisi keluar dibelokkan
180o, tentukan gaya untuk menahan elbow pada
tempatnya.

34. Soal: Pancaran Air Pada Plat Diam
• Kecepatan pancaran air
dari nozel adalah 20 m/s
dan menghantam plat
vertikal diam dengan laju
massa 10 kg/s. Setelah
mengenai plat, air
menyebar ke segala arah.
Tentukan gaya untuk
menahan plat agar tetap
diam di tempatnya.

35. • Asumsi:
1. Aliran air keluar dari nozel adalah stedi
2. Air menyebar ke segala arah setelah mengenai
plat dengan arah yang tegak lurus terhadap arah
pancaran air dari nozel
3. Pancaran air keluar ke atmosfer dan keluar dari
volume atur dengan tekanan atmosfer
4. Gaya-gaya vertikal dan fluks momentum
diabaikan karena tidak ada pengaruh pada arah
horizontal
5. Pengaruh faktor koreksi fluks momentum
diabaikan sehingga β ≈ 1

36. • Dengan
• maka
• dan
dan

37. Soal: Gaya Netto Pada Flens
• Laju aliran air: 18,5 gal/mnt,
• Diameter dalam sisi masuk: 0,780
in
• Tekanan di sisi masuk: 13,0 psig
• Berat kran + air di dalamnya: 12,0
lbf
• Alirannya stedi dan inkompresibel
• Diameter di sisi keluar = diameter
di sisi masuk
• β = 1,03
• Massa jenis air: 62,3 lbm/ft3
• Hitung gaya netto pada flens!

38. • Karena alirannya stedi dan inkompresibel maka:
• Persamaan momentum untuk aliran stedi:

40. Gerak Rotasi dan Momentum Sudut
• Gerak Benda Tegar (solid body)  Kombinasi
Gerak translasi pusat massa dan Gerak rotasi
terhadap pusat massa.
• Gerak translasi dapat dianalisa menggunakan
persamaan momentum,
• Besaran angular terdiri dari Jarak Angular,
Kecepatan Angular, dan Percepatan Angular.

41. • Keliling lingkaran  2πr
• Jarak angular 1 putaran  2π rad
• Maka, jarak yang ditempuh oleh
sebuah titik yang berputar sejauh θ
rad adalah l = θr
• θ adalah jarak angular dalam satuan
rad (radian), 1 rad = 360/2π ≈57,3o
• Kecepatan sudut (ω) dan
percepatan sudut (α) masingmasing adalah,
• V adalah kecepatan linier dan at
adalah percepatan linier dalam arah
tangensial.

42. •
•
Hukum Newton II mempersyaratkan
adanya gaya dalam arah tangensial yang
menyebabkan pecepatan sudut.
Kekuatan yang menyebabkan terjadinya
putaran disebut Momen atau Torsi.
•
Torsi total benda pejal yang berputar
terhadap sumbunya dinyatakan dengan,
•
I  momen inersia benda terhadap sumbu rotasi  ukuran kelembaman benda
terhadap putaran
Momen Gaya  hasil kali gaya dan jarak normal  rFt
Momen dari Momentum (Momentum Sudut)  hasil kali momentum dan jarak
normal  rmV = r2 mω
Momentum Sudut total benda pejal yang berputar terhadap sumbunya dinyatakan
dengan,
•
•
•

43. •
Kalau dinyatakan dalam vektor,
•
Persamaan Momentum Sudut:
•

M adalah torsi netto yang bekerja pada
benda yang berputar terhadap sumbunya.
•
Kecepatan sudut vs. Rpm (n),
•
Daya poros,
•
Energi kinetik rotasi total,
•
Percepatan sentripetal,

44. Persamaan Momentum Angular
• Momen dari Gaya,
• Besarnya,
• Momen dari Momentum
• Momen Angular (sistem),
• Laju perubahan Momen Angular

45. Persamaan Momentum Angular
• Persamaan Umum
• Untuk Volume Atur tetap,
• Untuk aliran stedi,
• Secara sederhana,
• Untuk aliran stedi,
• Untuk gaya-gaya dan aliran momentum pada
bidang yang sama

46. Soal
• Berat pipa horisontal + air
adalah 12 kg/m
• Tentukan momen lengkung
di titik A
• Tentukan panjang pipa
horisontal supaya momen di
titik A sama dengan 0.