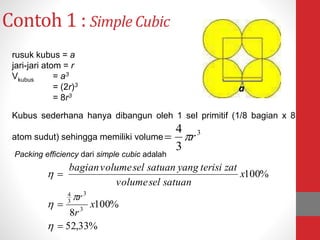
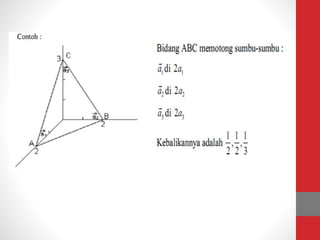
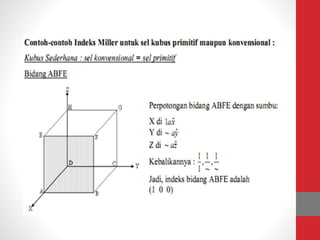
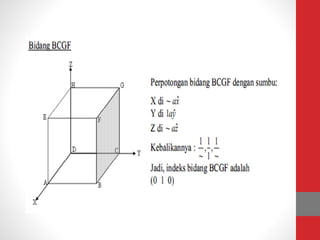
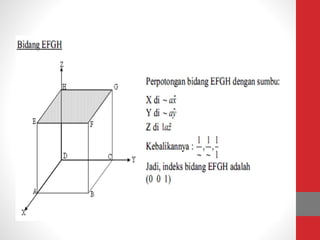
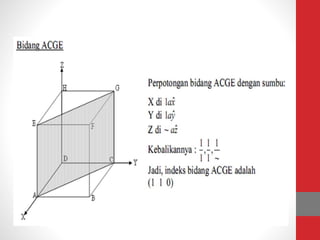
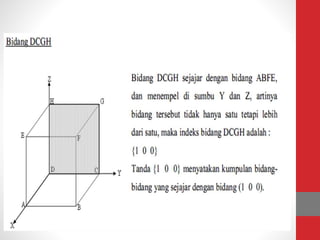
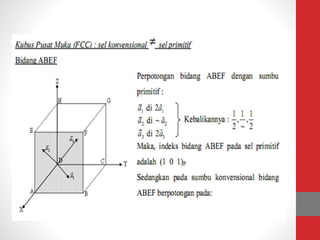
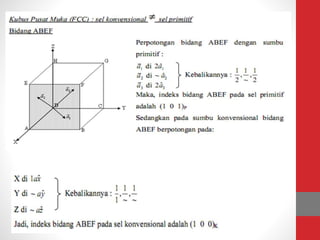
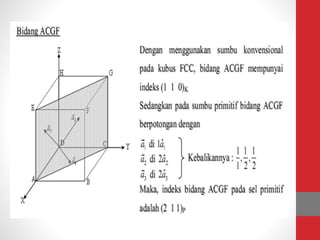
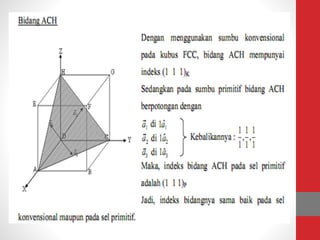
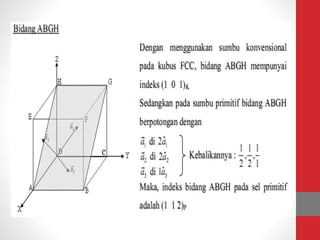
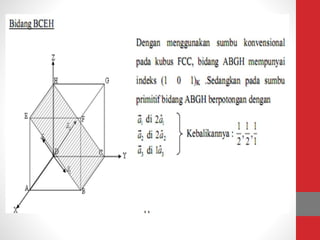
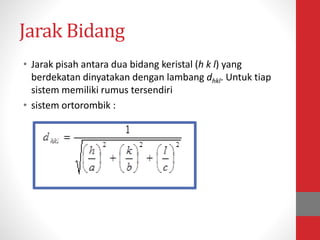
Dokumen tersebut memberikan ringkasan tentang tiga topik utama: (1) packing efisiensi untuk simple cubic, body centered cubic, dan face centered cubic; (2) penjelasan indeks Miller untuk menentukan orientasi bidang kristal; (3) rumus untuk menghitung jarak antar bidang kristal untuk berbagai sistem kristal.

1. Packing Efisiensi,
Indeks Miller,
Jarak Bidang
(4201410014) Bagus Purwo Nugroho
(42014100xx) Zuniar Musrifin
(4201410009) Malinda
(4201410025) Ratna Devi Cahyanti
(4201410058) Alfu Neizhela
(4201410073) Risky Fitri Aristia

2. Packing Efisiensi
kepadatan kekisi dinyatakan sebagai daya hasil
penjejalan (packing efisiensi).
Didefinisikan :

3. Contoh 1 : Simple Cubic
a
3
3
4
r
%33,52
%100
8
%100
3
3
3
4







x
r
r
x
satuanselvolume
zatterisiyangsatuanselvolumebagian
rusuk kubus = a
jari-jari atom = r
Vkubus = a3
= (2r)3
= 8r3
Kubus sederhana hanya dibangun oleh 1 sel primitif (1/8 bagian x 8
atom sudut) sehingga memiliki volume
Packing efficiency dari simple cubic adalah

4. Contoh 1 : Body Centered Cubic (BCC)
22 222
aaaa 
332 222
aaaa 
3a
3
4ra 
3
4r 3
39
64
r
3
3
8
r
%04,68
%100
39
64
3
8
%100
3
3







x
r
r
x
satuanselvolume
zatterisiyangsatuanselvolumebagian
rusuk kubus = a dan jari-jari atom = r
diagonal sisi kubus
diagonal ruang kubus
Pada BCC diagonal ruang mewakili 4 jari-jari atom
= 4r sehingga 4r = atau . Vkubus = a3 = ( )3 = . BCC
dibangun oleh 2 atom yaitu 1 atom pusat kubus dan 1 atom sudut ( 1/8 bagian x 8
atom sudut) memiliki volume . Didapat packing efficiency adalah

5. Contoh 1 : Face Centered Cubic/ FCC
22 222
aaaa 
%08,74
%100
2
32
3
16
%100
3
3







x
r
r
x
satuanselvolume
zatterisiyangsatuanselvolumebagian
rusuk kubus = a
jari-jari atom = r
diagonal sisi kubus
2a
2
4ra 
2
4r 3
2
32
r
3
3
16
r
Pada FCC diagonal ruang mewakili 4 jari-jari atom = 4r sehingga 4r =
atau . Vkubus = a3 = ( )3 = . FCC dibangun oleh 4 atom
yaitu, 3 atom muka kubus ( 1/2 bagian x 6 atom ) dan 1 atom sudut ( 1/8 bagian x
8 atom sudut ) memiliki volume . Didapat packing efficiency adalah

6. Indeks Miller
• Orientasi bidang-bidang kristal yang
ditentukan oleh tiga titik dalam bidang
(dikenal sebagai indeks Miller) dengan
notasi: (h k l).
• Digunakan untuk menyatakan bidang
kristal (indeks bidang)

7. Aturan :
1. Tentukan titik potong antara bidang yang
bersangkutan dengan sumbu-sumbu (a1, a2, a3) /
sumbu-sumbu primitif dalam satuan konstanta
lattice (a1, a2, a3)
2. Tentukan kebalikan dari bilangan-bilangan tadi
dan kemudian tentukan tiga bilangan bulat
(terkecil) yang mempunyai perbandingan yang
sama. Indeks (h k l)
Indeks Miller

9. Jika ketiga bilangan bulat yang mempunyai
perbandingan yang sama seperti diatas adalah 3, 3, 2.
dengan demikian indeks bidang ABC tersebut adalah
(3 3 2).
Perhatikan bahwa dalam penulisan indeks kita tidak
menggunakan tanda koma.
Misal :
(3 3 2)
h k l

22. Jarak Bidang
• Jarak pisah antara dua bidang keristal (h k l) yang
berdekatan dinyatakan dengan lambang dhkl. Untuk tiap
sistem memiliki rumus tersendiri
• sistem ortorombik :

23. • sistem kubik :
Sistem Tetragonal :
Sistem Hexagonal :
dhkl =
dhkl =
dhkl = 2
2
22
)()(
3
4
1
c
l
a
khkh



24. • Sistem trigonal :
• Sistem Monoklin :
• Sistem Triklin :
dhkl =
dhkl =
dhkl =
hlsklshkslskshs
V
132312
2
33
2
22
2
11 222 

25. Keterangan :
V = volume sel satuan
s11 = b2 c2 sin2a
s22 = b2 c2 sin2b
s33 = b2 c2 sin2g
s12 = a b c2 (cosa cosb - cosg)
s23 = a2 b c (cosb cosg - cosa)
s13 = a b2 c (cosg cosa - cosb)

26. THANKS FOR YOUR ATTENTION ....