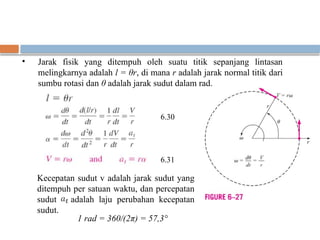
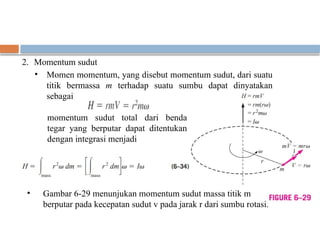
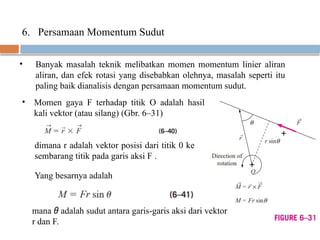
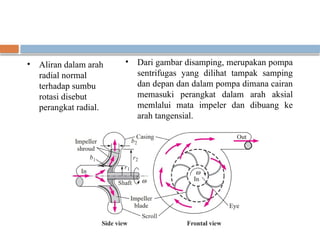
Dokumen ini membahas dinamika fluida, khususnya gerak rotasi dan momentum sudut, dengan penekanan pada analisis gerak rotasi benda tegar dan konsep-konsep seperti momen, torsi, dan energi kinetik rotasi. Selain itu, dijelaskan juga persamaan momentum sudut yang penting dalam berbagai masalah teknik dan bagaimana menghitung torsi dan energi yang terlibat dalam sistem aliran. Contoh aplikasi praktis seperti pompa sentrifugal dan sprinkler rumput juga diuraikan untuk menggambarkan prinsip-prinsip ini.