Downloaded 65 times
![preliminaries
Formal definition of Dominates (≪)
Given a set of d-dimensional points 푇
We say that a point t1 ∈ 푇 DOMINATES another point t2 ∈ 푇
If and only if
∀푖 ∈ 1, 2, 3, … , 푑 , 푡1 푖 ≧ 푡2[푖]
∃푗 ∈ 1, 2, 3, … , 푑 , 푡1 푗 > 푡2[푗]
and Denoted by t2 ≪ t1
(simply saying, t1 이 이득)
Definition from http://www.comp.nus.edu.sg/~atung/publication/k_dominant.pdf
Note that
the meaning of ‘dominates’ may differ
according to type of application](https://image.slidesharecdn.com/anoptimalandprogressivealgorithmforskylinequeriesslide-141208231153-conversion-gate01/85/An-optimal-and-progressive-algorithm-for-skyline-queries-slide-6-320.jpg)
Uploaded byWooSung Choi
An optimal and progressive algorithm for skyline queries slide
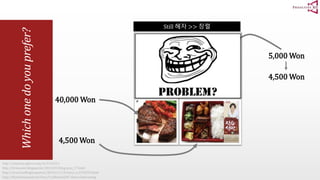
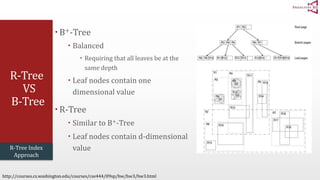
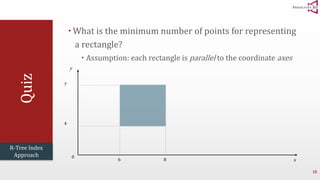
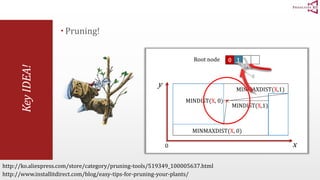
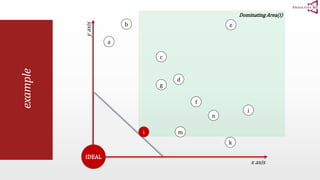
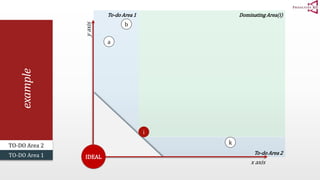
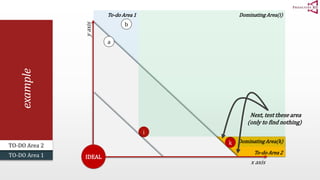
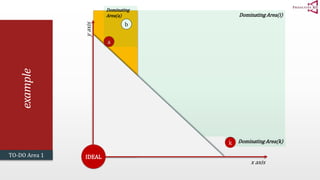
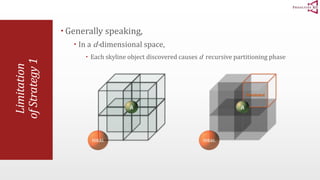
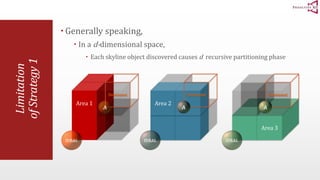
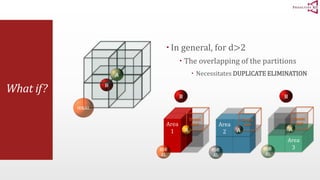
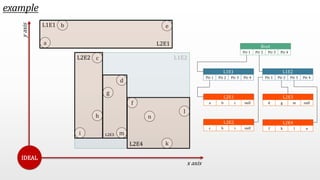
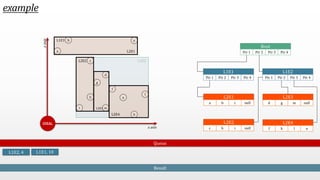
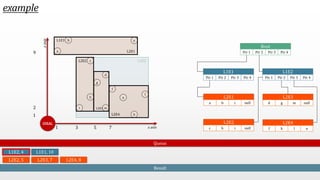
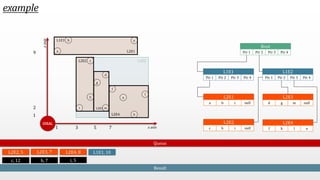
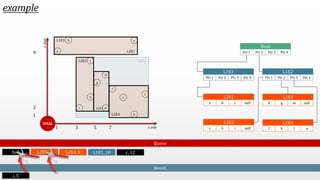
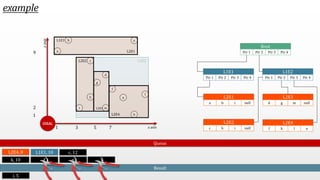
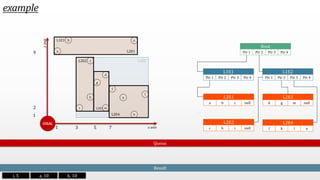
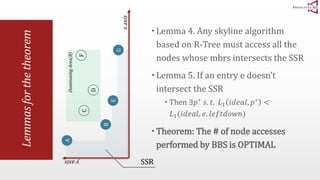
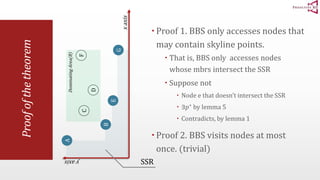
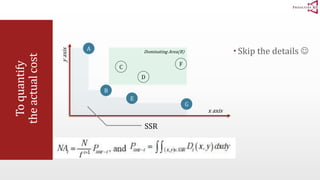
The document presents an optimal and progressive algorithm for processing skyline queries using an R-tree index. It discusses two strategies - recursive nearest neighbor queries and a branch and bound skyline algorithm. The recursive NN query approach requires additional processing to eliminate duplicate results for higher dimensions, while the branch and bound skyline algorithm prunes non-skyline points during traversal to directly generate the skyline without duplicates. The algorithm processes the R-tree in a best-first manner by maintaining a priority queue of tree nodes ordered by their minimum possible skyline size.
![Enterprise Java (November – 2018) [Choice Based | Question Paper]](https://cdn.slidesharecdn.com/ss_thumbnails/ej-cbcs-nov-2018-qp-191111054920-thumbnail.jpg?width=640&height=640&fit=bounds)
An optimal and progressive algorithm for skyline queries slide
- 1. INI Lab. AnOptimal and Progressive Algorithm for Skyline Queries Dimitris Papadias, Yufei Tao, Greg Fu, Bernhard Seeger ACM SIGMOD’ 2003 Presenters KYEONG SEOK HYUN, WOO-SUNG CHOI, JA-YEON KIM,
- 2. Abstract AnOptimal and Progressive Algorithm for Skyline Queries Using R-Tree
- 3. contents 1.Introduction 2. Related Work 2.1 Block Nested Loop (BNL) 2.5 Nearest Neighbor (NN) 3. Branch and Bound Skyline Algorithm With I/O analysis 5. Experimental Evaluation
- 4.
- 5. Which one doyou prefer? http://emperia.egloos.com/m/2516211 http://drmoontv.blogspot.kr/2013/03/blog-post_17.html http://www.huffingtonpost.kr/2014/11/13/story_n_6150254.html 5,000 Won 40,000 Won 4,500 Won http://flickrhivemind.net/User/Trollface%20T-Shirts/Interesting 혜자 >> 창렬
- 6. preliminaries Formal definitionof Dominates (≪) Given a set of d-dimensional points 푇 We say that a point t1 ∈ 푇 DOMINATES another point t2 ∈ 푇 If and only if ∀푖 ∈ 1, 2, 3, … , 푑 , 푡1 푖 ≧ 푡2[푖] ∃푗 ∈ 1, 2, 3, … , 푑 , 푡1 푗 > 푡2[푗] and Denoted by t2 ≪ t1 (simply saying, t1 이 이득) Definition from http://www.comp.nus.edu.sg/~atung/publication/k_dominant.pdf Note that the meaning of ‘dominates’ may differ according to type of application
- 7. Which one doyou prefer? http://emperia.egloos.com/m/2516211 http://drmoontv.blogspot.kr/2013/03/blog-post_17.html http://www.huffingtonpost.kr/2014/11/13/story_n_6150254.html 5,000 Won 40,000 Won 4,500 Won 4,500 Won http://flickrhivemind.net/User/Trollface%20T-Shirts/Interesting Still 혜자 >> 창렬
- 8. Hotel(attraction, 1/price,1/distance) Two Hotel A : `80`, `1/15,000`, `1/500m` B : `30`, `1/20,000`, `1/1500m` 퐵 ≪ 퐴 Why? 30<80 1/20,000 < 1/15,000 1/1,500m < 1/500m A 1/price attraction B Dominates! ≪ B A for example,
- 9. Very important ProblemDefinition (mathematical) The Skyline operator Input - Given a set of objects P = {푝1, 푝2, … , 푝푁} Output – {푝푖 | 푝푖 ∈ 푃 푎푛푑 ∄ 푝∗ ∈ 푃 푠. 푡. 푝푖 ≪ 푝∗} A B C Dominating Area(B) D E F “퐵 ∈ 푂푢푝푢푡, s푖푛푐푒 푛표 표푡ℎ푒푟 푝표푖푛푡 푃 ≫ 퐵”, correct x axis y axis G Common misconceptions “퐵 ∈ 푂푢푝푢푡 s푖푛푐푒 퐵 ≫ 퐶 , D, F” , wrong
- 10. Naïve approach forprocessing skyline queries
- 11. Exhaustive Test Suppose there are n objects in the given set 퐷푥 = {표1, 표2, … , 표푛} Algorithm -Naïve 1 푓표푟 푒푎푐ℎ 표푏푗푒푐푡 표푥 ∈ 퐷 푏표표푙푒푎푛 푖푠퐷표푚푖푛푎푡푒푑 = 푓푎푙푠푒 푓표푟 푒푎푐ℎ 표푏푗푒푐푡 표푦 ∈ 퐷 푖푓 ¬(표푥 = 표푦) 퐴푁퐷 ¬ 표푥 ≪ 표푦 푡ℎ푒푛 푐표푛푡푖푛푢푒; 푒푙푠푒 푡ℎ푒푛 푖푠퐷표푚푖푛푎푡푒푑 = 푡푟푢푒; break; 푖푓 ! 푖푠퐷표푚푖푛푎푡푒푑 푆 ∪ {표푥} A B F C D G E
- 12. Suppose thereare n objects in the given set 퐷푥 = {표1, 표2, … , 표푛} Algorithm -Naïve 1 푓표푟 푒푎푐ℎ 표푏푗푒푐푡 표푥 ∈ 퐷 푏표표푙푒푎푛 푖푠퐷표푚푖푛푎푡푒푑 = 푓푎푙푠푒 푓표푟 푒푎푐ℎ 표푏푗푒푐푡 표푦 ∈ 퐷 푖푓 ¬(표푥 = 표푦) 퐴푁퐷 ¬ 표푥 ≪ 표푦 푡ℎ푒푛 푐표푛푡푖푛푢푒; 푒푙푠푒 푡ℎ푒푛 푖푠퐷표푚푖푛푎푡푒푑 = 푡푟푢푒; break; 푖푓 ! 푖푠퐷표푚푖푛푎푡푒푑 푆 ∪ {표푥} Exhaustive Test Nested Loop Structure Modification: (Algorithm -Naïve 2) Idea 1. Use Nested Loop Structure Idea 2. Take advantage of ‘Block-transfer’ towards better re-usability! Block A Block B A B C D E F G The Inherited Limitation of these approaches 1. It needs full-scan over the data 2. Though, query result contains only a small fraction of the dataset 3. That is, these approaches are wasteful
- 13. R-Tree Index Approach for processing skyline queries
- 14. Preliminaries R-Tree Nearest Neighbor Query
- 15. Preliminaries R-Tree: Balancedtree for indexing multi-dimensional object Support Dynamic operation (insert, update, delete) R-Tree Index Approach
- 16. R-Tree VS B-Tree B+-Tree Balanced Requiring that all leaves be at the same depth Leaf nodes contain one dimensional value R-Tree Similar to B+-Tree Leaf nodes contain d-dimensional value R-Tree Index Approach http://courses.cs.washington.edu/courses/cse444/09sp/hw/hw3/hw3.html
- 17. Spatial objects (ord-dimensional objects or geometric objects) d-dimensional object? R-Tree Used for the Organization of a set of d-dimensional objects How? Main Idea Minimum Bounding Rectangles (MBRs) <Objects in 2-dimension space> http://caversham.otago.ac.nz/research/geog.php
- 18. Quiz What isthe minimum number of points for representing a rectangle? Assumption: each rectangle is parallel to the coordinate axes 18 6 8 7 4 x y 0 R-Tree Index Approach
- 19.
- 20. Nearest Neighbor (NN) Query Processing using R-Tree Nearest Neighbor Query Input Given a set of objects P = {푝1, 푝2, … , 푝푁} Query Point - q Output – {푝푖 | 푝푖 ∈ 푃 푎푛푑 ∄ 푝∗ ∈ 푃 푠. 푡. 퐿푝 푝푖 , 푞 > 퐿푝(푝∗, 푞)} 0 x y See how it works in appendix R-Tree Index Approach
- 21. Root node 01 MINMAXDIST(X,1) 0 x y MINDIST(X, 0) MINDIST(X,1) MINMAXDIST(X, 0) Key IDEA! Pruning! http://ko.aliexpress.com/store/category/pruning-tools/519349_100005637.html http://www.installitdirect.com/blog/easy-tips-for-pruning-your-plants/
- 22.
- 23. Back to theoriginal question Skyline with R-Tree
- 24. R-Tree Index Approach Let’s process skyline objects using R-Tree Strategy 1 – Use traditional tech. (i.e. NN Query) Strategy 2 – This paper Strategy 1 Partition the data using NN Query recursively Distance metric: 퐿1 푛표푟푚 First NN Query -> start from the ideal point (i.e. zero point)
- 25. Strategy 1 RecursiveNN Query
- 26. Dominating Area(i) example a x axis y axis b c d e f g i m n k i IDEAL
- 27. To-do Area 1 To-do Area 2 example a x axis y axis b i k IDEAL Dominating Area(i) TO-DO Area 2 TO-DO Area 1
- 28. Next, test thesearea (only to find nothing) To--do Arrea 2 To-do Area 1 example a x axis y axis b i k Dominating Area(i) TO-DO Area 2 TO-DO Area 1 Dominating Area(k) IDEAL ` `
- 29. To-do Area 1 example x axis i k Dominating Area(i) TO-DO Area 1 Dominating Area(k) a To-do Area 1 y axis b IDEAL Dominating Area(a)
- 30. Dominating Area(k) Result Dominating Area(i) IDEAL Dominating Area(a) x axis y axis i k a
- 31. Limitation of Strategy1 Generally speaking, In a d-dimensional space, Each skyline object discovered causes d recursive partitioning phase Dominated
- 32. Limitation of Strategy1 Generally speaking, In a d-dimensional space, Each skyline object discovered causes d recursive partitioning phase Area 1 Dominated Area 2 Dominated Dominated Area 3
- 33. What if? In general, for d>2 The overlapping of the partitions Necessitates DUPLICATE ELIMINATION Area 1 Domin ated Area 2 Domin ated Domin ated Area 3
- 34. Disadvantage ! Strategy 1 needs an additional phase For removing redundant outputs 4 elimination methods Laisser-faire Propagate Merge Fine-grained Partitioning They works Problem: sub-optimal
- 35. Strategy 2 Branch& Bound Skyline Algorithm
- 36. Idea! Similarto previous NN Query Branch & Bound Skyline (BBS) http://greatleadersserve.org/leadership/big-idea-great-leaders-serve/
- 37. h example a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n
- 38. example h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 L1E1 L1E2 Queue L1E2, 4 L1E1, 10 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n Result
- 39. example h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 9 L1E2, 4 L1E2 Queue L2E2, 5 3 5 7 L1E1, 10 L2E3, 7 L2E4, 8 2 1 1 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n Result
- 40. example h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n Queue 3 5 7 9 2 1 1 L2E2, 5 L2E3, 7 L2E4, 8 L1E1, 10 c, 12 h, 7 i, 5 Result
- 41. example h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n Queue 3 5 7 9 2 1 1 i, 5 h, 7 L2E4, 8 L1E1, 10 c, 12 Result L2E3, 7
- 42. example h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n Queue 3 5 7 9 2 1 1 h, 7 L2E4, 8 L1E1, 10 c, 12 i, 5 Result L2E3, 7
- 43. example h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n Queue 3 5 7 9 2 1 1 L2E4, 8 L1E1, 10 c, 12 i, 5 Result k, 10 f n i
- 44. example h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 Root Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E1 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L1E2 Ptr 1 Ptr 2 Ptr 3 Ptr 4 L2E1 a b c null L2E2 c h i null L2E3 d g m null L2E4 f k l n Queue 3 5 7 9 2 1 1 i, 5 Result a, 10 k, 10
- 45.
- 46. Analysis of Strategy1 Notation Variable Description s #of Skyline obj e Empty Query ne Non-empty Query r Redendent Query d d-dimension h Height of the given R-Tree Recursion Tree … d new recursive NN … … 푛푒 = 푠 + 푟 푒 = 푛푒 ∙ 푑 − 1 + 1, 푠푖푛푐푒 푛푒 + 푒 = 푛푒 ∙ 푑 + 1(푟표표푡) 푒 = 푠 + 푟 푑 − 1 + 1 푁퐴푁푁 ≥ 푒 + 푠 + 푟 ∗ ℎ = 푠 + 푟 푑 − 1 + 1 + 푠 + 푟 ℎ > 푠 ∙ ℎ ∙ 푑
- 47.
- 48. Analysis of Strategy2 (brief version) Notation Variable Description s #of Skyline obj h Height of the given R-Tree 푠 ∙ ℎ ≥ 푁퐴퐵퐵푆 푁퐴푁푁 > 푠 ∙ ℎ ∙ 푑 > 푁퐴퐵퐵푆
- 49. Is it theoptimal solution? BBS Algorithm
- 50. Proof 1. Termination & Correctness Lemma 1. BBS visits entries in ascending order Of their distance to the ‘ideal point’ Lemma 2. Any data point added into Result_Set Is guaranteed to be a final skyline point Proof. Suppose not then 푝푗 was added into Result_Set but not a final skyline point Then, ∃ 푝∗ ∈ 퐷퐵 푠. 푡, 푝∗ ≫ 푝푗 , which means L1 ideal, p∗ < L1(ideal, pj) However, observe that 푝∗ must be visited before 푝푗 by lemma 1. Contradiction: 푝푗 should have been pruned, which contradicts the assumption. Lemma 3. All data point will be examined, unless one of its ancestor nodes has been pruned.
- 51. Lemmas for thetheorem Lemma 4. Any skyline algorithm based on R-Tree must access all the nodes whose mbrs intersects the SSR Lemma 5. If an entry e doesn’t intersect the SSR Then ∃푝∗ 푠. 푡. 퐿1 푖푑푒푎푙, 푝∗ < 퐿1(푖푑푒푎푙, 푒. 푙푒푓푡푑표푤푛) Theorem: The # of node accesses performed by BBS is OPTIMAL Dominating Area(B) A B F C D E x axis y axis G SSR
- 52. Proof of thetheorem Proof 1. BBS only accesses nodes that may contain skyline points. That is, BBS only accesses nodes whose mbrs intersect the SSR Suppose not Node e that doesn’t intersect the SSR ∃푝∗ by lemma 5 Contradicts, by lemma 1 Proof 2. BBS visits nodes at most once. (trivial) Dominating Area(B) A B F C D E x axis y axis G SSR
- 53. To quantify theactual cost A Skip the details B C Dominating Area(B) D E F x axis y axis G SSR
- 54.
- 55.
- 56.
- 57. Cardinality 3ddataset
- 58. Progressive behavior N=1M, d=3
- 59. Constrained skyline queries N=1M, d=3 h a x axis y axis b c d e f g i m n k l IDEAL L1E2 L1E1 L2E4 L2E2 L2E3 L2E1 Constrain