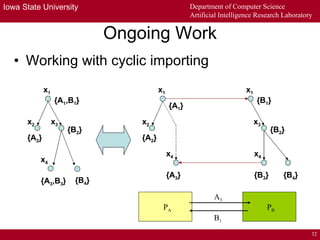
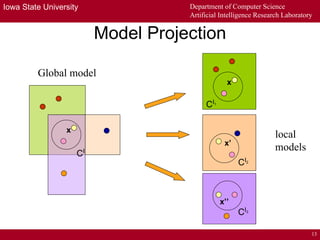
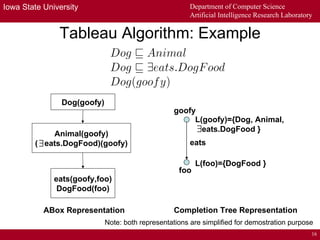
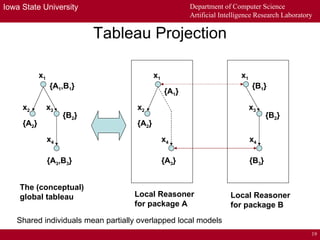
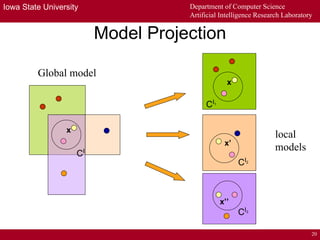
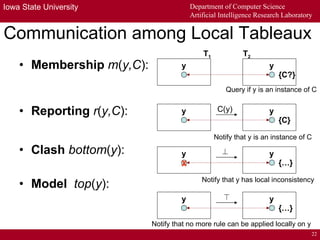
The document describes a distributed tableau algorithm for reasoning with modular ontologies expressed in Package-based Description Logics (P-DL). The algorithm uses multiple local reasoners, each maintaining a local tableau for a single ontology module. Local reasoners communicate by querying each other or reporting clashes to collectively construct a global tableau without fully integrating the modules. The algorithm is proven sound and complete for P-DL with acyclic module importing. It can support reasoning across modules to answer queries.

1. A Distributed Tableau Algorithm for Package-based Description Logics Jie Bao 1 , Doina Caragea 2 and Vasant G Honavar 1 1 Artificial Intelligence Research Laboratory, Department of Computer Science, Iowa State University, Ames, IA 50011-1040, USA. {baojie, honavar}@cs.iastate.edu 2 Department of Computing and Information Sciences Kansas State University, Manhattan, KS 66506, USA dcaragea@ksu.edu 2nd International Workshop on Context Representation and Reasoning (CRR 2006) @ ECAI 2006, Aug 29, 2006, Riva del Garda, Italy

2. Dr. D. Caragea Dr. V. Honavar Jie Bao

3. Outline Requirements for reasoning with modular ontologies Package-based Description Logics (P-DL): features and semantics A tableau algorithm for (P-DL) ALCP C Discussions

4. Modularity

5. The Need for Modular Ontologies(MO) Collaborative Ontology Building Distributed Data Management Large Ontology Management Partial Ontology Reuse

6. Reasoning with MO If GraduateOK(Jie) is consistent with the ontology? (If Jie can graduate?) Computer Science Dept Ontology Registration Office Ontology Semantic Relations Bob = 3304 G r a d u a t e O K v : 9 f a i l s : C o r e C o u r s e G r a d u a t e O K v P r e l i m O K P r e l i m O K ( J i e ) C s C o r e C o u r s e v C o r e C o u r s e C s C o r e C o u r s e ( c s 5 1 1 ) f a i l s ( 3 3 0 4 ; c s 5 1 1 ) S S N ( 3 3 0 4 ; 1 2 3 4 5 6 7 8 9 )

7. Reasoning with MO (2) Major Consideration: should not require the integration of ontology modules. High communication cost High local memory cost May violate module autonomy, e.g., privacy Question: can we do reasoning for modular ontologies without (syntactic level) an integrated ontology ? (semantic level) a (materialized) global tableau ?

8. Outline Requirements for reasoning with modular ontologies Package-based Description Logics (P-DL): features and semantics A tableau algorithm for (P-DL) ALCP C Discussions

9. Package A package is an ontology module that captures a sub-domain; Each term has a home package A package can import terms from other packages Package extension is denoted as P P C :Package extension with only concept name importing E.g., ALCP C = ALC + P C General Pet Wild Livestock Animal ontology PetDog Pet Dog General

10. Package: Example O 1 (General Animal) O 2 (Pet) It uses ALCP, but not ALCP C

11. Semantics of Importing Domain relations are compositionally consistent : r 13 =r 12 O r 23 Therefore domain relations are transitively reusable. Domain relation : individual correspondence between local domains Importing establishes one-to-one domain relations “ Copies” of individuals are shared x x’ Δ I 1 Δ I 2 C I 1 C I 2 r 12 Δ I 3 r 13 r 23 x’’ C I 3

12. Partially Overlapping Models x x’ Δ I 1 Δ I 2 C I 1 C I 2 Δ I 3 r 13 r 23 x’’ C I 3 x C I Global interpretation obtained from local Interpretations by merging shared individuals r 12

13. Model Projection x C I x C I 1 x’ C I 2 x’’ C I 3 Global model local models

14. Outline Requirements for reasoning with modular ontologies Package-based Description Logics (P-DL): features and semantics A tableau algorithm for (P-DL) ALCP C Discussions

15. Tableau Algorithm A tableau is a representation of a model Basic idea: start with some initial facts for an ontology use tableau expansion rules to infer new facts, until no rule can be applied, or inconsistencies are found among those facts. If a clash-free fact set is found, a model of the ontology is constructed

16. Tableau Algorithm: Example Dog(goofy) Animal(goofy) ( eats.DogFood)(goofy) eats(goofy,foo) DogFood(foo) goofy L(goofy)={Dog, Animal, eats.DogFood } foo L(foo)={DogFood } eats ABox Representation Completion Tree Representation Note: both representations are simplified for demostration purpose

17. Federated Reasoning Chef: Hello there, children! Where does Kyle move to? Chef: We are in South Park, Colorado; San Francisco is in California; Colorado is far from California. Stan: So they are far from us. Too Bad. Stan: Hey, Chef . Is Kyle’s new home far from us? Cartman: San Francisco, I guess.

18. Federated Reasoning for P-DL Basic strategy Use multiple local reasoners, each for a single package Each local reasoner creates and maintains a local tableau based on local knowledge A local reasoner may query other reasoners if its local knowledge is incomplete Global relation among tableaux is created by messages (1) (2) (3) (4)

19. Tableau Projection x 1 {A 1 } {A 2 } {A 3 } x 2 x 4 x 1 {B 1 } {B 3 } {B 2 } x 3 x 4 The (conceptual) global tableau Local Reasoner for package A Local Reasoner for package B Shared individuals mean partially overlapped local models x 1 {A 1 ,B 1 } {A 2 } {A 3 ,B 3 } {B 2 } x 2 x 3 x 4

20. Model Projection x C I x C I 1 x’ C I 2 x’’ C I 3 Global model local models

21. Tableau Expansion Tableau Expansion for ALCP C with acyclic importing

22. Communication among Local Tableaux Membership m ( y,C ): Reporting r ( y,C ): Clash bottom ( y ): Model top ( y ): y y {C?} y y {C} C(y) y y {…} y y {…} X Query if y is an instance of C Notify that y is an instance of C Notify that y has local inconsistency Notify that no more rule can be applied locally on y T 1 T 2

23. ALCP C Expansion Example Consistency of the ontology is witnessed by P 1 y is the shared individual Subset blocking is still applicable E.g. L 1 (y)  L 1 (x) x L 1 (x)={A,  R.B} y y z L 2 (y)={B,  P.C} L 2 (z)={C,  P.C} R P T 1 T 2 L 1 (y)={A,  R.B} w L 2 (w)={C,  P.C} P P 1 P 2 > v 1 : A ; > v 9 ( 1 : R ) : ( 2 : B ) > v ( 2 : P ) : ( 2 : C )

24. ALCP C Expansion Example (2) P 1 : 1:A 1:B P 2 : 1:B 2:C P 3 : 2:C 3:D Query: if A D (from the point of view of P 3 ) (it is not answerable by either DDL nor E-Connection in their current forms) Reasoning: if A D is not true, then there will be clash. Hence, it must be true L 3 (x)={ A⊓  D ,  C⊔D A,  C,  D} Transitive Subsumption Propagation T 3 x r(x,  C ) x x r(x,A) T 2 T 1 L 2 (x)={  B⊔C  C ,  B} L 1 (x)={  A⊔B A ,  B , B } r(x,  B )  (x)  (x)  (x)

25. ALCP C Expansion Example (3) L 2 (x)={ P,  P⊔B,  P⊔  F,B,  F} x x L 1 (x)={ B,  F ,  B⊔F, F } T 2 T 1 r(x,B) r(x,  F)  (x) L 1 (x)={A,  A⊔C,C} y z L 2 (y)={A,  A⊔  R.B,  B⊔(A⊓  C),  R.B,  B} P T 1 T 2 L 2 (z)={B,  A⊔  R.B,  B⊔(A⊓  C),  R.B, A⊓  C, A,  C} y L 1 (z)={A,  C ,  A⊔C, C } z r(z,A) r(z,  C)  (x) r(z,A) (x)  Detect Inter-module Unsatisfiability 2:P is unsatisfiable Reasoning from Local Point of View 1:A is unsatisfiable witnessed by P 2 is satisfiable witnessed by P 1 P 1 : f 1 : B v 1 : F g , P 2 : f 1 : P v 1 : B ; 2 : P v : 1 : F g P 1 : f 1 : A v 1 : C g P 2 : f 1 : A v 9 2 : R : ( 2 : B ) ; 2 : B v 1 : A u ( : 1 : C ) g

26. Soundness β α α α α β α or or α A A A B A’ A’’ A’ A B’ infer (a) Augmenting (c) Reporting (b) Searching A is consistent iff A’ is consistent A is consistent iff A’ is consistent or A’’ is consistent (A,B) is consistent iff (A,B’) is consistent send

27. Completeness P-DL model can be constructed from a distributed Tableau

28. Termination Acyclic importing ensures no message loop Blocking Subset blocking Reporting blocking: A node is temporarily blocked after sending a reporting message x y y z T 1 T 2 w T 3 z v P 1 P 3 P 2 import import Tableaux Ontology

29. Outline Requirements for reasoning with modular ontologies Package-based Description Logics (P-DL): features and semantics A tableau algorithm for (P-DL) ALCP C Discussions

30. Other Tableau Projections Distributed Description Logics (DDL) [ Serafini and Tamilin 2004, 2005] x 1 x 2 x 3 x 4 x 1 x 2 x 3 x 4 x 3 x 5 x 5 f B 1 u : B 2 ; ¢ ¢ ¢ g f B 1 u : B 2 ; ¢ ¢ ¢ g

31. Other Tableau Projections (2) x 1 x 2 x 3 x 4 x 1 x 2 x 4 x 5 x 3 x 6 E-Connections [ Grau 2005] x 5 x 6 E E {A 1 } {A 1 } {A 2 } {A 3 } {B 1 } {B 2 } {B 3 } {A 2 } {A 3 } {B 1 } {B 2 } {B 3 }

32. Ongoing Work Working with cyclic importing x 1 {A 1 ,B 1 } {A 2 } {A 3 ,B 3 } {B 2 } x 2 x 3 x 4 x 1 {A 1 } {A 2 } {A 3 } x 2 x 4 x 1 {B 1 } {B 3 } {B 2 } x 3 x 4 {B 4 } {B 4 } B 1 A 3 P A P B

33. Ongoing Work (2) Asynchronous reasoning: local reasoners don’t need to wait after a reporting message Thus they can concurrently search on different branches for a possible global tableau. Working with OWL Support SHOIQ(D) Implementation based on Pellet

34. References P-DL: J. Bao, D. Caragea, and V. Honavar. Towards collaborative environments for ontology construction and sharing. In International Symposium on Collaborative Technologies and Systems (CTS 2006) . 2006. J. Bao, D. Caragea, and V. Honavar. Modular ontologies - a formal investigation of semantics and expressivity. 2006. In the Asian Semantic Web Conference (ASWC), LNCS 4185, pp. 616–631, 2006. J. Bao, D. Caragea, and V. Honavar. On the Semantics of Linking and Importing in Modular Ontologies. accepted by the International Semantic Web Conference (ISWC) 2006. (In Press) J. Bao, D. Caragea, and V. Honavar. A tableau-based federated reasoning algorithm for modular ontologies. Submitted to 2006 IEEE/WIC/ACM International Conference on Web Intelligence, 2006 (under reviewing) Related work: L. Serafini and A. Tamilin. Local tableaux for reasoning in distributed description logics. In Description Logics Workshop 2004, CEUR-WS Vol 104 , 2004. L. Serafini and A. Tamilin. Drago: Distributed reasoning architecture for the semantic web. In ESWC , pages 361-376, 2005. B. C. Grau. Combination and Integration of Ontologies on the Semantic Web . PhD thesis, Dpto. de Informatica, Universitat de Valencia, Spain, 2005.

35. Thanks !

36. Reasoning by Model Construction Model x Man I Human I If such a model is not possible in any situation, Man <= Human is true Reasoning Suppose it is not true, then at least one individual x in a world (model) is Man but not Human To query Man Human If such a model can be constructed, then Man <= Human is not true