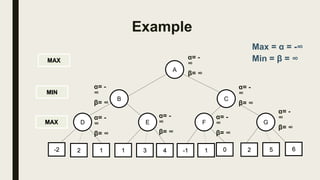
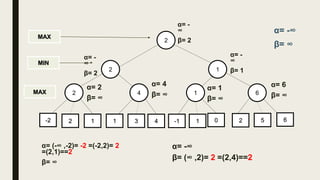
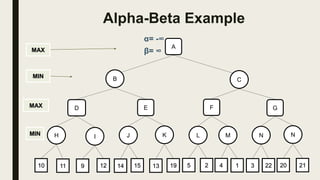
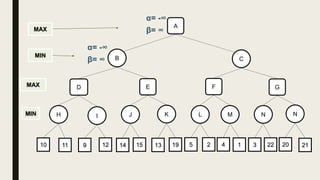
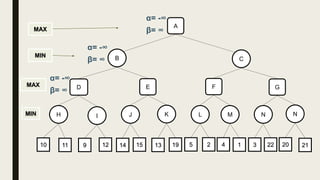
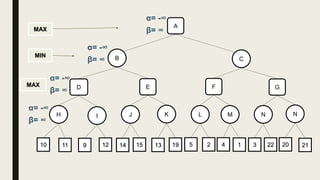
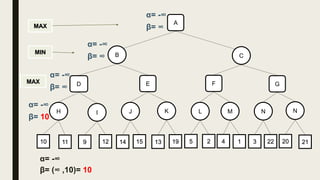
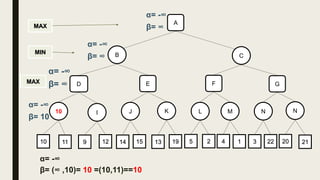
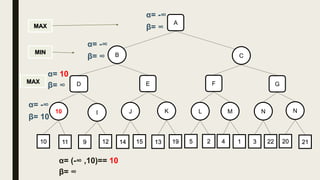
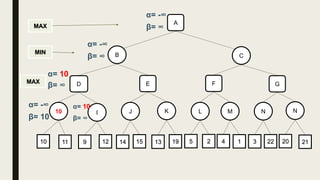
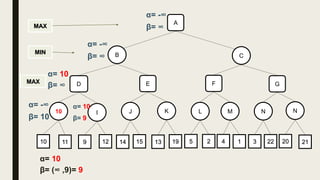
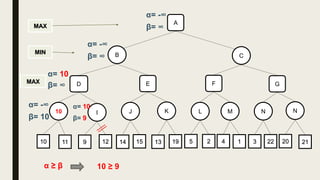
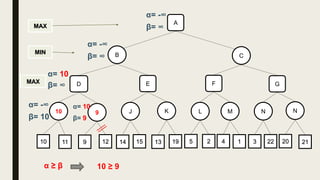
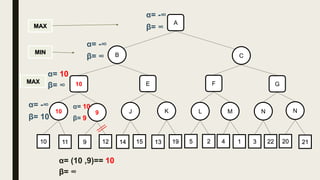
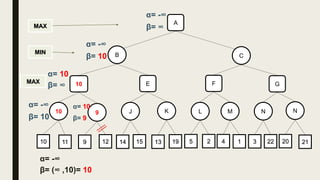
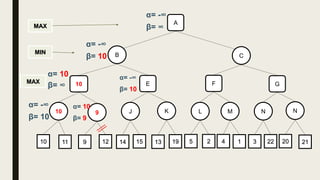
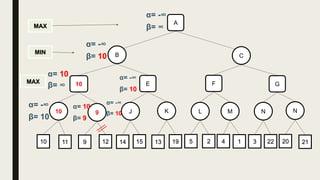
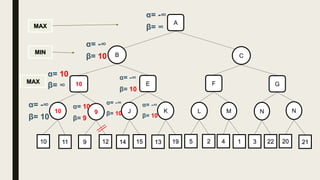
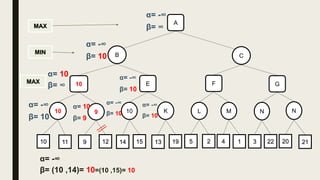
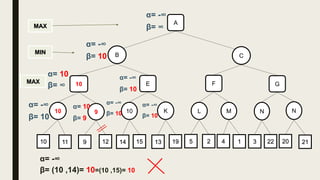
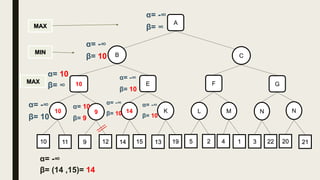
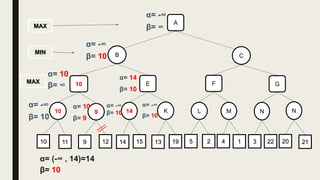
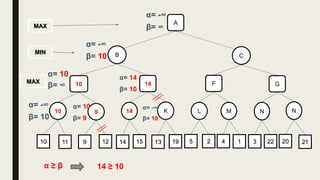
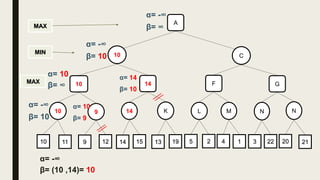
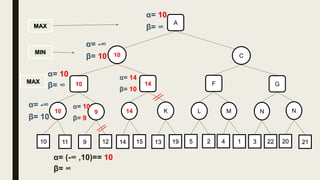
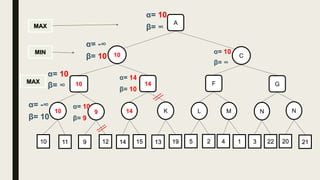
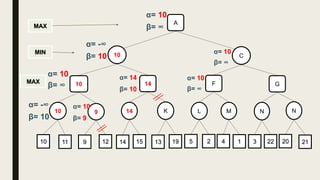
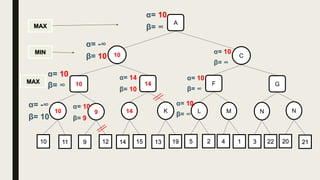
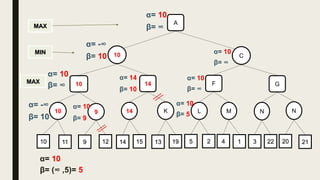
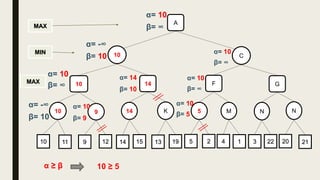
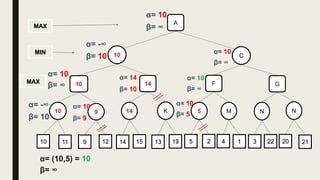
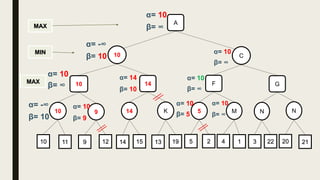
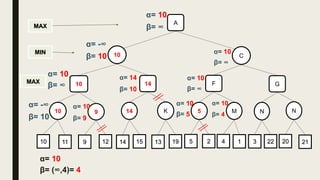
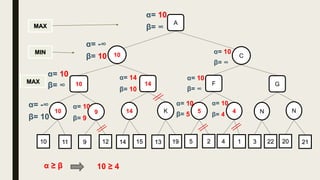
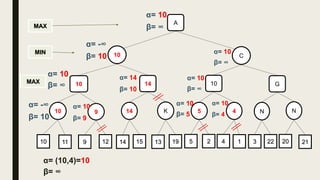
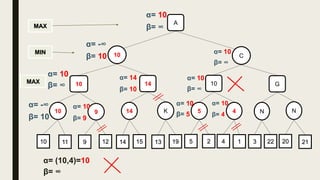
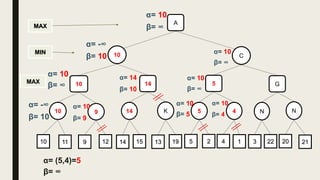
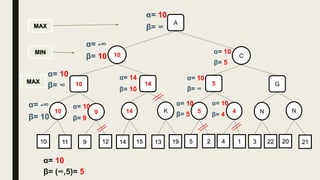
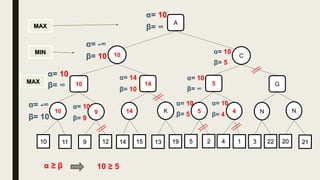
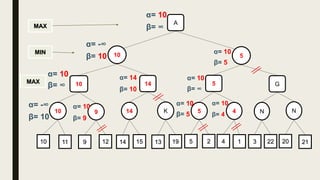
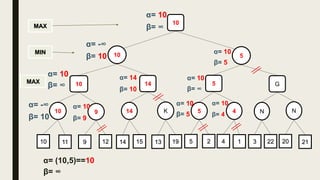
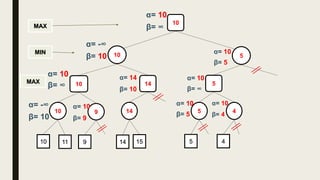
Alpha-beta pruning is a search algorithm used to reduce the number of nodes evaluated in a minimax search tree for machine playing of two-player games. It uses two values - alpha (the best value for MAX) and beta (the best value for MIN) - to prune subtrees without affecting the result when alpha is greater than or equal to beta. The algorithm traverses the search tree depth-first, updating alpha and beta at each node to cut off subtrees that won't influence the final value. This pruning technique preserves the optimality of minimax while evaluating fewer nodes.

1. ALPHA BETA
PRUNING
PRESENTED BY: RAHABUL ISLAM

2. Introduction
 Alpha–beta pruning is a search algorithm that seeks to
decrease the number of nodes that are evaluated by the
minimax algorithm in its search tree. It is an adversarial
search algorithm used commonly for machine playing of
two-player games (Tic-tac-toe, Chess, Go, etc)
 Alpha-beta pruning gets its name from two parameters. –
They describe bounds on the values that appear anywhere
along the path under consideration:
α = the value of the best (i.e., highest value) choice
found so far along the path for MAX .
β = the value of the best (i.e., lowest value) choice
found so far along the path for MIN.

3. Games (Tic-tac-toe, Chess, Go, etc)

4. Minimax Algorithm
 Assign a initial value to each possible ending.
 Assures best possible ending, assuming opponent also plays
perfectly.
 opponent tries to give you worst possible ending.
 Depth-first search tree traversal that updates initial values as
it recourses back up the tree.
 Time complexity O(b^m)

5. Example
A
B C
GFED
-2 1 1 4 -1 0 2 6
MIN
MAX
2 3 1 5
MAX
α= -
∞
β= ∞
α= -
∞
β= ∞
α= -
∞
β= ∞
α= -
∞
β= ∞
α= -
∞
β= ∞
α= -
∞
β= ∞
α= -
∞
β= ∞
Max = α = -∞
Min = β = ∞

6. 2
2 1
6142
-2 1 1 4 -1 0 2 6
MIN
MAX
MAX
2 3 1 5
α= -
∞
β= 2
α= -
∞
β= 1
α= 2
β= ∞
α= -
∞
β= 2
α= 4
β= ∞
α= 6
β= ∞
α= 1
β= ∞
α= (-∞ ,-2)= -2 =(-2,2)= 2
=(2,1)==2
β= ∞
α= -∞
β= (∞ ,2)= 2 =(2,4)==2
α= -∞
β= ∞

7. Alpha-Beta Pruning
 Avoid processing subtrees that have no effect on the result
 Two new parameters
• α: The best value for MAX seen so far
• β: The best value for MIN seen so far
 α is used in MIN nodes, and is assigned in MAX nodes
 β is used in MAX nodes, and is assigned in MIN nodes
 When maximizing, cut off values lower than Alpha
 When minimizing, cut off values greater than Beta

8. When to Prune
Prune whenever α ≥ β
 Prune below a Max node whose alpha value becomes greater than
or equal to the beta value of its ancestors.
• Max nodes update alpha based on children’s returned
values.
 Prune below a Min node whose beta value becomes less than or
equal to the alpha value of its ancestors.
• Min nodes update beta based on children’s returned values.

9. Properties of α-β
 Pruning preserves completeness and optimality of original
minimax algorithm
 Good move ordering improves effectiveness of pruning
 With "perfect ordering," time complexity = O(b^m/2)
Therefore, doubles depth of search

10. Alpha-beta Algorithm
 Depth first search
– only considers nodes along a single path from root at any time
α = highest-value choice found at any choice point of path for MAX
(initially, α = −infinity)
β = lowest-value choice found at any choice point of path for MIN
(initially, β = +infinity)
 Pass current values of α and β down to child nodes during search.
 Update values of α and β during search:
– MAX updates α at MAX nodes
– MIN updates β at MIN nodes
 Prune remaining branches at a node when α ≥ β

11. Initial Assumption
 At the start of the problem, you see only the current state. As
for upper and lower bounds, all you know is that it's a number
less than infinity and greater than negative infinity. Thus,
here's what the initial situation looks like:
≥-∞
≤ ∞
Max = α = -∞
Min = β = ∞

12. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJIH NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
MIN
A
GFED
Alpha-Beta Example

13. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJIH NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
MIN
A
α= -∞
β= ∞
GFED

14. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJIH NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
MIN
A
α= -∞
β= ∞
GFED
α= -∞
β= ∞

15. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJIH NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= -∞
β= ∞
α= -∞
β= ∞

16. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJIH NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= -∞
β= ∞
α= -∞
β= 10
α= -∞
β= (∞ ,10)= 10

17. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJI10 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= -∞
β= ∞
α= -∞
β= 10
α= -∞
β= (∞ ,10)= 10 =(10,11)==10

18. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJI10 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= 10
β= ∞
α= -∞
β= 10
α= (-∞ ,10)== 10
β= ∞

19. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJI10 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= ∞

20. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJI10 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 10
β= (∞ ,9)= 9

21. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJI10 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α ≥ β 10 ≥ 9

22. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJ910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFED
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α ≥ β 10 ≥ 9

23. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJ910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= ∞
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= (10 ,9)== 10
β= ∞

24. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJ910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= -∞
β= (∞ ,10)= 10

25. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJ910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= -∞
β= 10

26. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJ910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= -∞
β= 10
α= -∞
β= 10

27. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
KJ910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= -∞
β= 10
α= -∞
β= 10
α= -∞
β= 10

28. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
K10910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= -∞
β= (10 ,14)= 10=(10 ,15)= 10
α= -∞
β= 10
α= -∞
β= 10
α= -∞
β= 10

29. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
K10910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= -∞
β= (10 ,14)= 10=(10 ,15)= 10
α= -∞
β= 10
α= -∞
β= 10
α= -∞
β= 10

30. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= -∞
β= (14 ,15)= 14
α= -∞
β= 10
α= -∞
β= 10
α= -∞
β= 10

31. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GFE10
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= -∞
β= 10
α= (-∞ , 14)=14
β= 10
α= -∞
β= 10

32. B C
10
MIN
MAX
MAX
α= -∞
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= -∞
β= 10
α ≥ β 14 ≥ 10

33. 10 C
10
MIN
MAX
MAX
α= -∞
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= -∞
β= (10 ,14)= 10

34. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= (-∞ ,10)== 10
β= ∞

35. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞

36. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞

37. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= ∞

38. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NML N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= 10
β= (∞ ,5)= 5

39. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NM5 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α ≥ β 10 ≥ 5

40. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NM5 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= (10,5) = 10
β= ∞

41. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NM5 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= 10
β= ∞

42. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 NM5 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= 10
β= (∞,4)= 4
α= 10
β= 4

43. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
GF1410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4
α ≥ β 10 ≥ 4

44. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
G101410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4
α= (10,4)=10
β= ∞

45. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
G101410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4
α= (10,4)=10
β= ∞

46. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
G51410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= ∞
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4
α= (5,4)=5
β= ∞

47. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
G51410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= 5
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4
α= 10
β= (∞,5)= 5

48. 10 C
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
G51410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= 5
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4
α ≥ β 10 ≥ 5

49. 10 5
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
A
α= -∞
β= 10
G51410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= 5
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4

50. 10 5
10
MIN
MAX
MAX
α= 10
β= ∞
K14910 N45 N
11 9 12 22314 15 13 19 5 2 4 1 20 21
10
α= -∞
β= 10
G51410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= 5
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4
α= (10,5)==10
β= ∞

51. 10 5
10
MIN
MAX
MAX
α= 10
β= ∞
14910 45
11 9 14 15 5 4
10
α= -∞
β= 10
51410
α= 10
β= ∞
α= -∞
β= 10
α= 10
β= 9
α= 14
β= 10
α= 10
β= 5
α= 10
β= ∞
α= 10
β= 5
α= 10
β= 4

52. CODE
// C++ program to demonstrate working of Alpha-Beta Pruning
#include<bits/stdc++.h>
using namespace std;
//# Initial values of Aplha and Beta
const int MAX = 1000;
const int MIN = -1000;
// Returns optimal value for current player (Initially called
// for root and maximizer)
int minimax(int depth, int nodeIndex, bool maximizingPlayer,
int values[], int alpha, int beta)
{
// Terminating condition. i.e leaf node is reached
if (depth == 3)

53. return values[nodeIndex];
if (maximizingPlayer)
{
int best = MIN;
// Recur for left and right children
for (int i=0; i<2; i++)
{
int val = minimax(depth+1, nodeIndex*2+i,
false, values, alpha, beta);
best = max(best, val);
alpha = max(alpha, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
else
{
int best = MAX;

54. // Recur for left and right children
for (int i=0; i<2; i++)
{
int val = minimax(depth+1, nodeIndex*2+i,
true, values, alpha, beta);
best = min(best, val);
beta = min(beta, best);
// Alpha Beta Pruning
if (beta <= alpha)
break;
}
return best;
}
}
int main()
{
int values[8] = { 3, 5, 6, 9, 1, 2, 0, -1 };
cout << "The optimal value is : "
<< minimax(0, 0, true, values, MIN, MAX);;
return 0;
}

55. Conclusion
 Minimax finds optimal play for deterministic, fully observable,
two-player games
 Alpha-Beta reduction makes it faster

56. THANK YOU