Downloaded 42 times
Uploaded byFela Aziiza
Aljabar linear 2
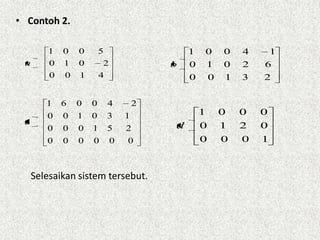
Dokumen tersebut membahas tentang eliminasi Gaussian dan sistem persamaan linear homogen. Secara ringkas, eliminasi Gaussian adalah prosedur untuk mengubah sistem persamaan ke bentuk eselon dengan menghilangkan unsur-unsur di atas utama 1 menjadi nol, sedangkan sistem persamaan linear homogen memiliki hanya variabel tetapi tanpa konstanta, sehingga selalu memiliki penyelesaian trivial.
More Related Content
Aljabar linear 2
- 1. ALJABAR LINEAR ELIMINASI GAUSSIAN Disusun Oleh : ANNISA SEFTIKA FIKRI 10130024 LIA ASTRIANA 10130164 RIA AGUSTINA 10130265 OKTO BERIANTO 10130237
- 2. A. BENTUK ESELONBARIS TEREDUKSI Sebuah matriks harus mempunyai sifat-sifat berikut ini: • Jika suatu baris tidak seluruhnya terdiri dari nol, maka angka tak nol pertama dalam baris tersebut adalah sebuah angka 1. (Kita sebut ini utama 1) • Jika ada sembarang baris yang seluruhnya terdiri dari nol, maka baris-baris ini dikelompokkan bersama di bagian bawah matriks. • Jika sembarang dua baris yang berurutan yang tidak seluruhnya terdiri dari nol, utama 1 dalam baris yang lebih bawah terletak di sebelah kanan utama 1 dalam baris yang lebih atas. • Masing-masing kolom yang berisi sebuah utama 1 mempunyai nol di tempat lainnya.
- 3. Suatu matriks yangmempunyai sifat 1, 2, dan 3 (tetapi tidak perlu 4) disebut matriks berbentuk eselon baris. • Contoh 1. Matriks-matriks berikut ini berada dalam bentuk eselon baris tereduksi. 0 1 2 0 1 1 0 0 4 1 0 0 0 0 0 1 3 0 0 0 1 0 7 0 1 0 , 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 Matriks-matriks berikut ini berada dalam bentuk eselon baris, tetapi bukan dalam bentuk eselon baris tereduksi 1 4 3 7 1 1 0 0 1 2 6 0 0 1 6 2 0 1 0 0 0 1 1 0 0 0 1 5 0 0 0 0 0 0 0 1
- 4. • Contoh 2. 1 0 0 5 1 0 0 4 1 a 0 1 0 2 b 0 1 0 2 6 0 0 1 4 0 0 1 3 2 1 6 0 0 4 2 0 0 1 0 3 1 1 0 0 0 c d 0 1 2 0 0 0 0 1 5 2 0 0 0 0 0 0 0 0 0 1 Selesaikan sistem tersebut.
- 5. B. Eliminasi Gaussian Langkah1. Tempatkan kolom paling kiri yang tidak seluruhnya terdiri dari nol. Langkah 2. Pertukarkan baris teratas dengan baris lainnya, jika perlu, untuk membawa salah satu entri tak nol ke posisi paling atas dari kolom yang didapatkan dalam Langkah 1 Langkah 3. Jika entri yang sekarang berada di posisi paling atas pada kolom yang ditemukan dalam Langkah 1 adalah a, kalikan baris pertama dengan 1/a untuk mendapatkan utama 1 Langkah 4. Tambahkan hasil kali yang sesuai dari baris teratas ke baris-baris di bawahnya sedemikian sehingga semua entri di bawah utama 1 menjadi nol.
- 6. Langkah 5. Sekarangtutup baris teratas matriks tersebut dan mulai lagi dengan Langkah 1 yang diterapkan pada submatriks yang tersisa. Lanjutkan cara ini sampai semua matriks berada dalam bentuk eselon baris Langkah 6. Mulai dengan baris tak nol terakhir dan kerjakan ke atas, tambahkan perkalian yang sesuai dari masing-masing baris ke baris di atasnya untuk mendapatkan nol di atas utama 1 Jika kita hanya menggunakan lima langkah pertama, prosedur tersebut menghasilkan bentuk baris- eselon dan disebut Eliminasi Gaussian.
- 7. Contoh . Selesaikandengan eliminasi Gauss-Jordan x1 3x2 2 x3 2 x5 0 2x1 6x2 5x3 2x4 4x5 3x6 1 5x3 10x4 15x6 5 2x1 6x2 8x4 4x5 18x6 6
- 8. C. SUBTITUSI BALIK Systempersamaan yang berpadanan bisa diselesaikan dengan suatu teknik yang disebut substitusi-balik. Langkah-langkah: Langkah 1. Selesaikan persamaan pertama untuk peubah-peubah utama Langkah 2. Mulai dengan persamaan yang paling bawah dan lanjutkan ke atas, secara berturut-turut substitusikan setiap persamaan ke semua persamaan di atasnya Langkah 3. Tetapkan sembarang nilai untuk peubah-peubah bebas, jika ada.
- 9. Contoh. Selesaikan bentukbaris Eselon 1 3 2 0 2 0 0 0 0 1 2 0 3 1 1 0 0 0 0 0 1 3 0 0 0 0 0 0 0
- 10. D. SISTEM LINEARHOMOGEN • Suatu sistem persamaan linear dikatakan homogen jika semua konstantanya adalah nol; yaitu jika sistem tersebut mempunyai bentuk a11 x1 a12 x 2 a1nxn 0 a 21 x1 a 22 x 2 a 2 nxn 0 am1 x1 am 2 x 2 amnxn 0 Setiap sistem persamaan linear homogen mempunyai sifat konsisten, karena semua sistem seperti itu mempunyai0, , x 0 x 0, x 1 2 n sebagai penyelesaiannya. Penyelesaian ini disebut penyelesaian trivial; jika ada penyelesaian yang lain, maka penyelesaiannya disebut penyelesaian tak trivial.
- 11. Karena sistem linearhomogen selalu mempunyai penyelesaian trivial, hanya ada dua kemungkinan untuk penyelesaiannya. 1. Sistem tersebut hanya mempunyai satu penyelesaian trivial. 2. Sistem tersebut mempunyai tak hingga banyaknya penyelesaian di samping penyelesaian trivial. Dalam kasus khusus pada sistem linear homogen dari dua persamaan dengan dua peubah, katakanlah a1 x b1 y 0 (a2, b2 keduanya tidak nol) a2 x b2 y 0 (a1, b1 keduanya tidak nol)
- 12. grafik persamaannya berupagaris-garis yang melalui titik asal, dan penyelesaian trivialnya berpadanan dengan perpotongan di titik asal (Gambar 1). y ax+by 1 1 y dan a 2 x + b2 y a1 x b1 y 0 x x a 2 x b2 0 Gambar 1 Tak hingga banyaknya penyelesaian Tak hingga banyaknya penyelesaian Hanya satu penyelesaian trivial Ada suatu kasus dimana suatu sistem homogeny dijamin mempunyai penyelesaian tak trivial, yaitu jika sistem tersebut mencakup jumlah peubah yang lebih banyak daripada jumlah persamaannya
- 13. Contoh. Selesaikan sistem persamaanlinear homogeny berikut ini dengan eliminasi Gauss-Jordan. 2 x1 2 x 2 x 3 x5 0 (1) x1 x2 2 x 3 3x 4 x5 0 x1 x2 x3 x5 0 x3 x4 x5 0
- 14.