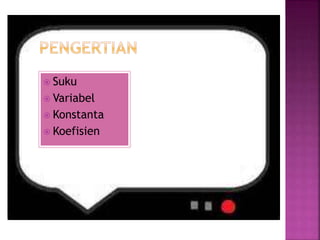
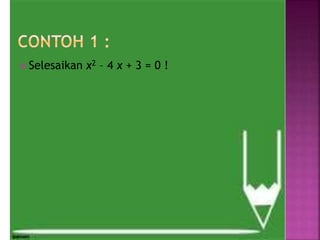
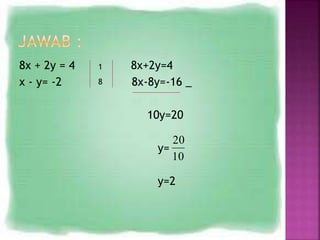Dokumen ini membahas konsep dasar aljabar, termasuk variabel, konstanta, koefisien, serta jenis-jenis persamaan matematis seperti persamaan linear dan kuadrat. Selain itu, dokumen juga menjelaskan metode penyelesaian persamaan, termasuk diskriminan, himpunan penyelesaian, dan sistem persamaan linier. Contoh perhitungan harga barang juga disertakan untuk menggambarkan penggunaan persamaan dalam kehidupan sehari-hari.

1. Veronica dewi setyorini 292011281
Puji astuti 292011285
Fitri helma sofi 292011287
Dedy yusuf 292011

2.  Suku
 Variabel
 Konstanta
 Koefisien

3.  Suku adalah variabel beserta koefisiennya
atau konstanta pada bentuk aljabar yang
dipisahkan oleh perasi jumlah atau selisih.

4.  Variabel adalah lambang pengganti suatu
bilangan yang belum diketahui nilainya
dengan jelas.

5.  Konstanta adalah suku dari suatu bentuk
aljabar yang berupa bilangan dan tidak
memuat variabel

6.  Koefisien adalah faktor konstanta dari suatu
suku pada bentuk aljabar

7.  Persaman adalah kalimat terbuka yang
mengandung hubungan sama dengan.

8.  Persamaan linear adalah persamaan yang
pangkat variabelnya adalah satu.
 Bentuk umum persamaan liner:
ax + b = c, a ≠ 0, a,b,c  R

9. Menyelesaikan persamaan linear
adalah mencari pengganti variabel
sehingga persamaan menjadi
pernyataan yang bernilai benar.
Contoh:
Selesaikan 3x + 4 =16 !
Jawab :
Agar 3x + 4 = 16 maka x diganti
dengan 4, jadi penyelesaiannya x = 4

10.  Pertidaksamaan adalah kalimat terbuka yang
menggunakan tanda <, > , ≤ , ≥.

11.  Pengertian persamaan kuadrat
Persamaan kuadrat di definisikan sebagai
kalimat terbuka yang menyatakan hubungan
sama dengan(=) dan pangkat tertinggi dari
peubah(variabel) adalah dua.
 Bentuk umum persamaan kuadrat sebagai
berikut :
ax2 + bx + c = 0

12.  memfaktorkan,
 melengkapkan kuadrat sempurna,
 menggunakan rumus

13.  ax2 + bx + c = 0 dapat dinyatakan menjadi a
(x – x1) (x – x2) = 0.
 Nilai x1 dan x2 disebut akar-akar
(penyelesaian) persamaan kuadrat.

14.  Selesaikan x2 – 4 x + 3 = 0 !

15. x2 – 4 x + 3 = 0
(x – 3)(x – 1)= 0
x – 3 = 0 atau x – 1 = 0
x = 3 atau x = 1
Jadi, penyelesaian dari x2 – 4 x + 3 = 0 adalah
3 dan 1.

16.  Tentukan himpunan penyelesaian dari (x – 2)2
= x – 2

17. (x – 2)2 = x – 2
x2 – 4 x + 4 = x – 2
x2 – 5 x + 6 = 0
(x – 3)(x – 2) = 0
x – 3 = 0 atau x – 2 = 0
x = 3 atau x = 2
Jadi, himpunan penyelesaiannya adalah {3 , 2}

18.  Persamaan kuadrat ax2 + bx + c = 0 dapat
diselesaikan dengan mengubahnya menjadi (x
+ p)2 = q.

19.  Tentukan himpunan penyelesaian dari x2 – 6 x
+ 5 = 0.

20.  x2 – 6 x + 5 = 0
 x2 – 6 x + 9 – 4 = 0
 x2 – 6 x + 9 = 4
 (x – 3)2 = 4
 x – 3 = 2 atau x – 3 = –2
 x = 5 atau x = 1
 Jadi, himpunan penyelesaiannya adalah{ 1 ,
5}.

21.  Rumus penyelesaian persamaan kuadrat
a x2 + b x + c = 0

22.  Tentukan himpunan penyelesaian dari x2 + 7x
– 30 = 0

23. x2 + 7x – 30 = 0
a = 1, b = 7, c = – 30
x = 3 atau x = –10
Jadi, himpunan penyelesaiannya adalah
{–10 , 3}.

24.  persamaan kuadrat ax2 + bx + c = 0 dengan
akar-akarnya , b2 – 4ac disebut diskriminan
(D).

25.  D > 0 merupakan bilangan real positif,
sehingga persamaan kuadrat mempunyai dua
akar real berlainan, .
 D = 0 maka persamaan kuadrat mempunyai
dua akar real sama. .
 D < 0 merupakan bilangan tidak real
(imajiner), maka persamaan kuadrat tidak
mempunyai akar real atau persamaan
kuadrat mempunyai akar tidak real.

26.  Tentukan jenis-jenis akar persamaan kuadrat
x2 + 5 x + 2 = 0

27. x2 + 5 x + 2 = 0
a = 1 , b = 5 , c = 2
D = b2 – 4ac = 52 – 4 . 1 . 2 = 25 – 8 = 17
Ternyata D>0. Jadi, persamaan x2+5x+2=0 mempunyai dua
akar real berlainan.

28. Tentukan jenis-jenis akar persamaan
kuadrat x2 + 5 x + 2 = 0

29. x2 – 10 x + 25 = 0
a = 1 , b = -10 , c = 25
D = b2 – 4ac = (-10)2 – 4 . 1 . 25 = 100 – 100 = 0
Karena D = 0, maka persamaan x2 -10x+25=0 mempunyai
dua akar real sama.

30.  Tentukan jenis-jenis akar persamaan kuadrat
3 x2 – 4 x + 2 = 0

31. 3 x2 – 4 x + 2 = 0
a = 3 , b = –4 , c = 2
D = b2 – 4ac = (-4)2 – 4 . 3 . 2 = 16 – 24 = – 8
Jadi, persamaan 3 x2 – 4 x + 2 = 0 tidak
mempunyai akar real.

32.  Pengertian sistem persamaan linier.
SPL adalah gabungan dua atau lebih
persamaan linier yang saling berkaitan satu
dengan yang lain.

33.  Sistem persamaan linier terbagi menjadi dua,
yaitu sistem persamaan linier dua peubah
dan sistem persamaan kinier tiga peubah

34.  Eliminasi
 Subtitusi
 Eliminasi da subtitusi
 grafik

35.  Berapakah himpunan dari penyelesaian :
8x + 2y = 4
x - y= -2

36. 8x + 2y = 4 8x+2y=4
x - y= -2 8x-8y=-16 _
10y=20
y=
y=2
1
8
10
20

37. 8x - 2y = 4 -8x+2y=4
x - y= -2 2x-2y=-4 _
-10x=0
x=
x= 0
Jadi himpunan penyelesaian dengan cara
eliminasi adalah 0,2
-1
2
10
0


38. Berapakah himpunan dari penyelesaian :
8x + 2y = 4
x - y= -2

39. 8x + 2y = 4
x - y= -2
Kita ambil satu saja misalnya x-y=-2, jadi
x-y=-2 x=-2+y
Kita masukkan x kedalam 8x+2y=4
8x+2y=4
8(-2+y)+2y=4
-16+8y+2y=4
10y = 4+16
10y=20
y =
y = 2
10
20

40.  y = 2
x-y=-2
x-2=-2
x=-2+2
x=0
Jadi himpunan penyelesaian dengan cara
subtitusi adalah 0,2

41.  Nia membeli 3 batang pensil dan 2 penggaris
dengan harga Rp6000,00. ditoko yang sama
Dewi memebeli 4 penggaris dan 1 buku
dengan harga Rp8000,00. Karena dewi pergi
dengan adiknya maka adiknya dibelikan 1
pensil dan 1 buku dengan harga Rp3000,00.
Berapakah harga 1 pensil, 1 penggaris, dan 1
buku ditoko tersebut?

42. Misal : pensil = x
penggaris = y
buku = z
Diket : 3x + 2y = 6000 persamaan 1
4y + z = 8000 persamaan 2
x + z = 3000 persamaan 3
Ditanya : x = ?
y = ?
z = ?

43. x + z = 3000
x= 3000 – z
Kemudian subtitusikan ke persaman 1
3x + 2y = 6000
3(3000-z) + 2y = 6000
9000-3z+2y=6000
-3z+2y=6000-9000
-3z+2y=-3000 atau 2y-3z= -3000( persamaan 4 )

44. 4y+z=8000 8y+2z = 16000
2y-3z=-3000 8y-12z =-12000 _
14z = 28000
z =
z = 2000
2
4
14
28000

45. x+z = 3000
x+2000=3000
x= 3000-2000
x= 1000

46. 4y+z=8000
4y+2000 = 8000
4y= 8000-2000
4y=6000
y=
y= 1500
4
6000

47.  Jadi harga satu pensil Rp 1000,00 , satu
penggaris Rp 1500,00 , satu buku Rp 2000,00

48. Terima kasih
