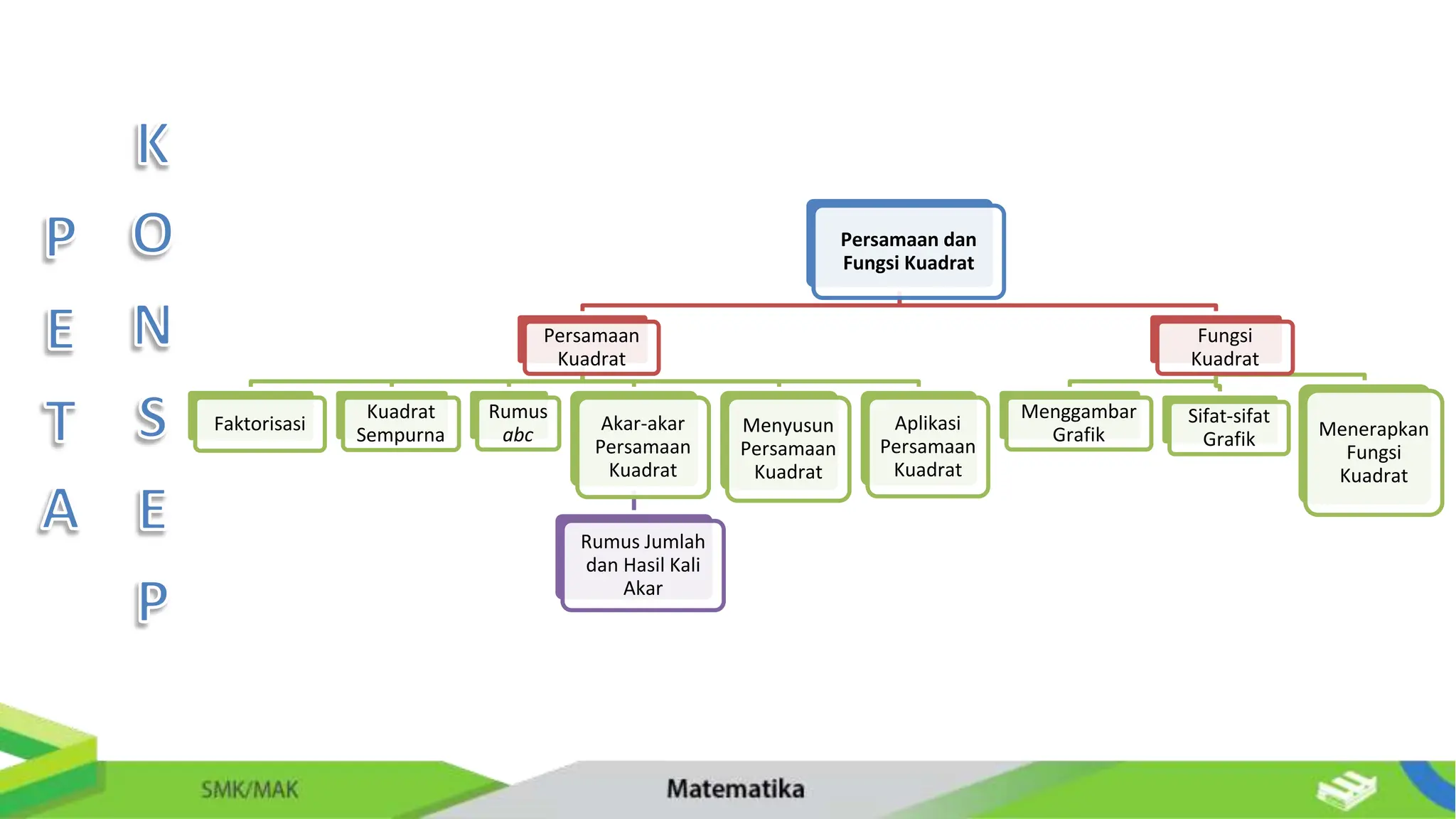
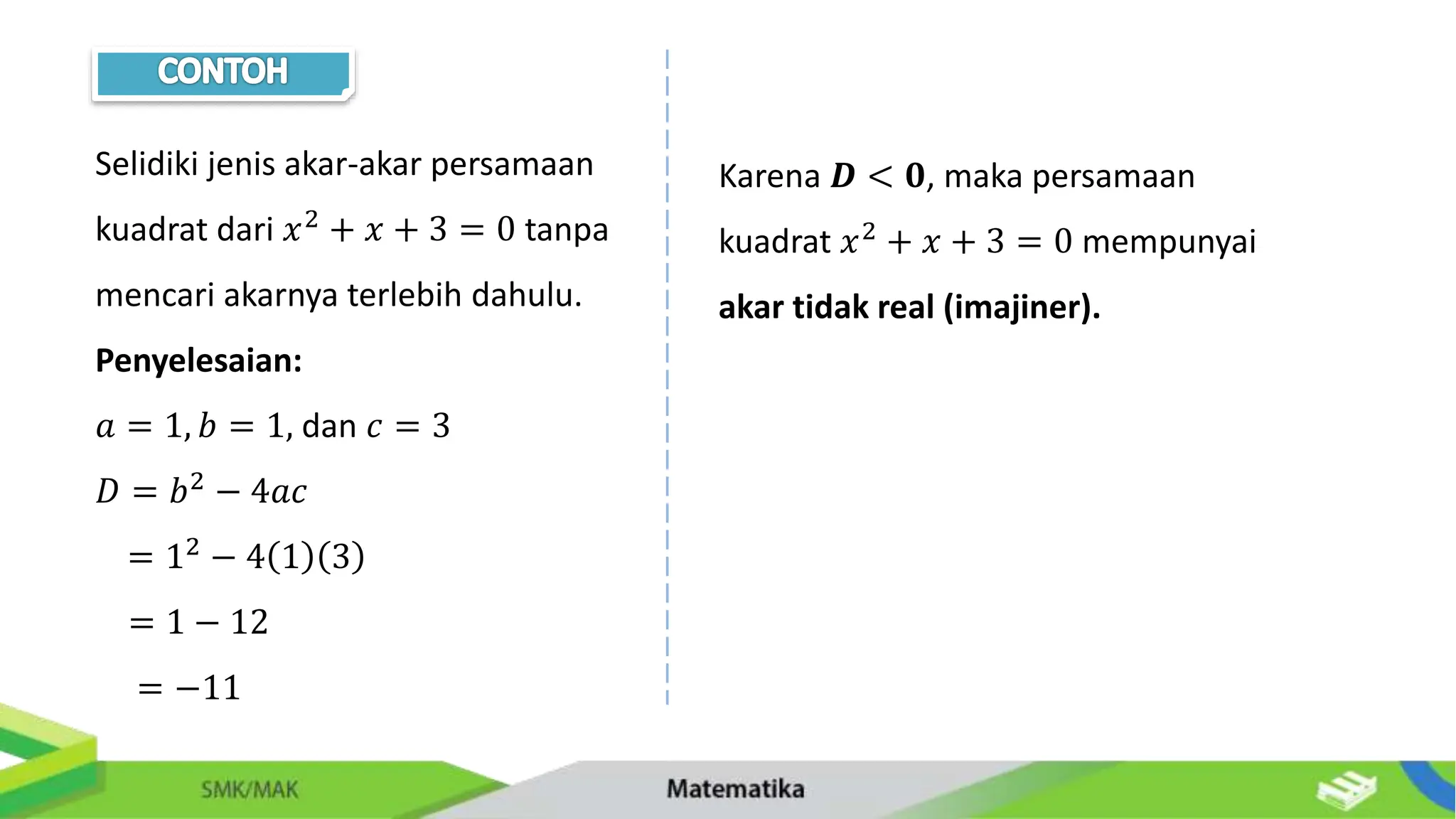
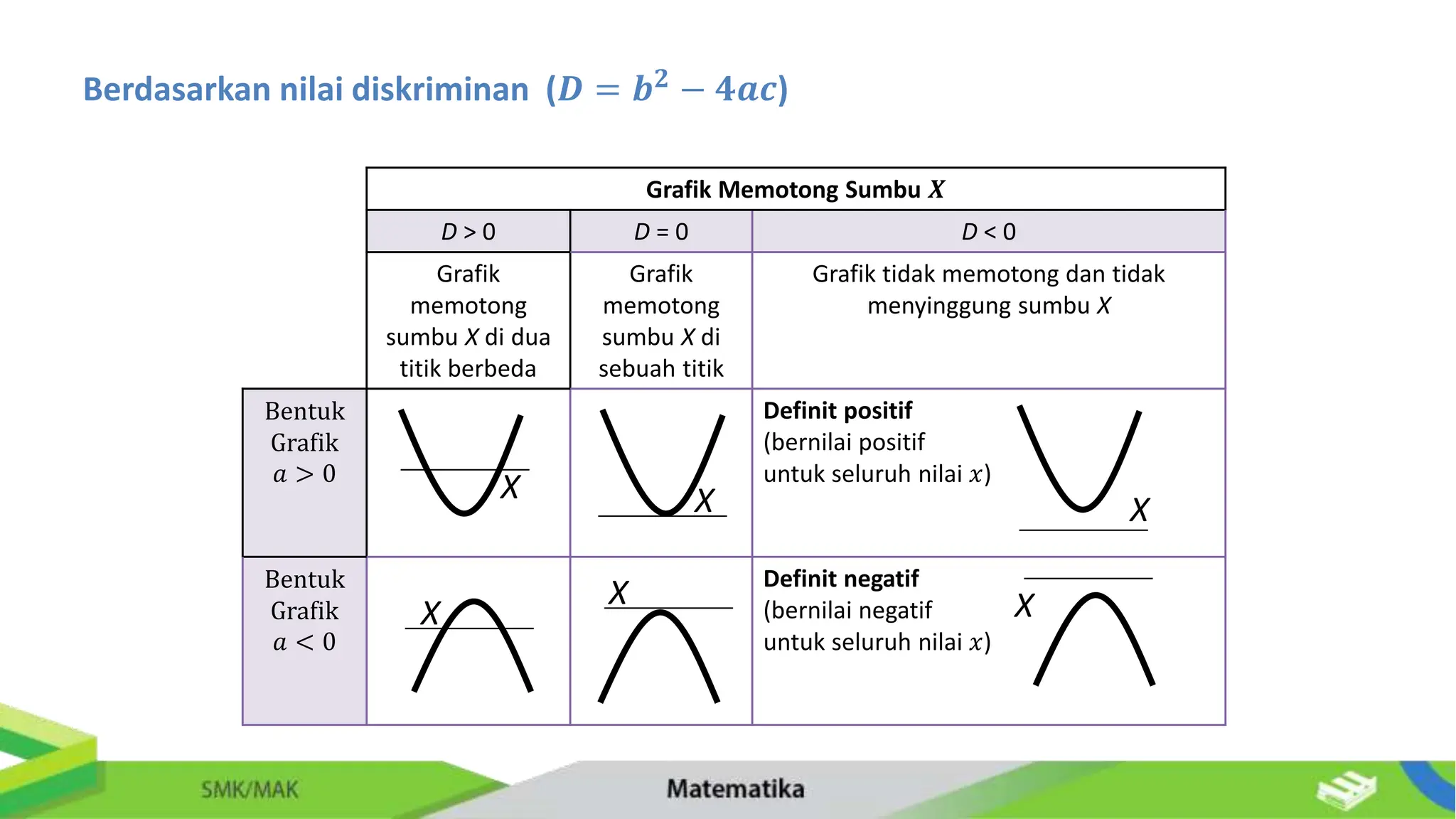
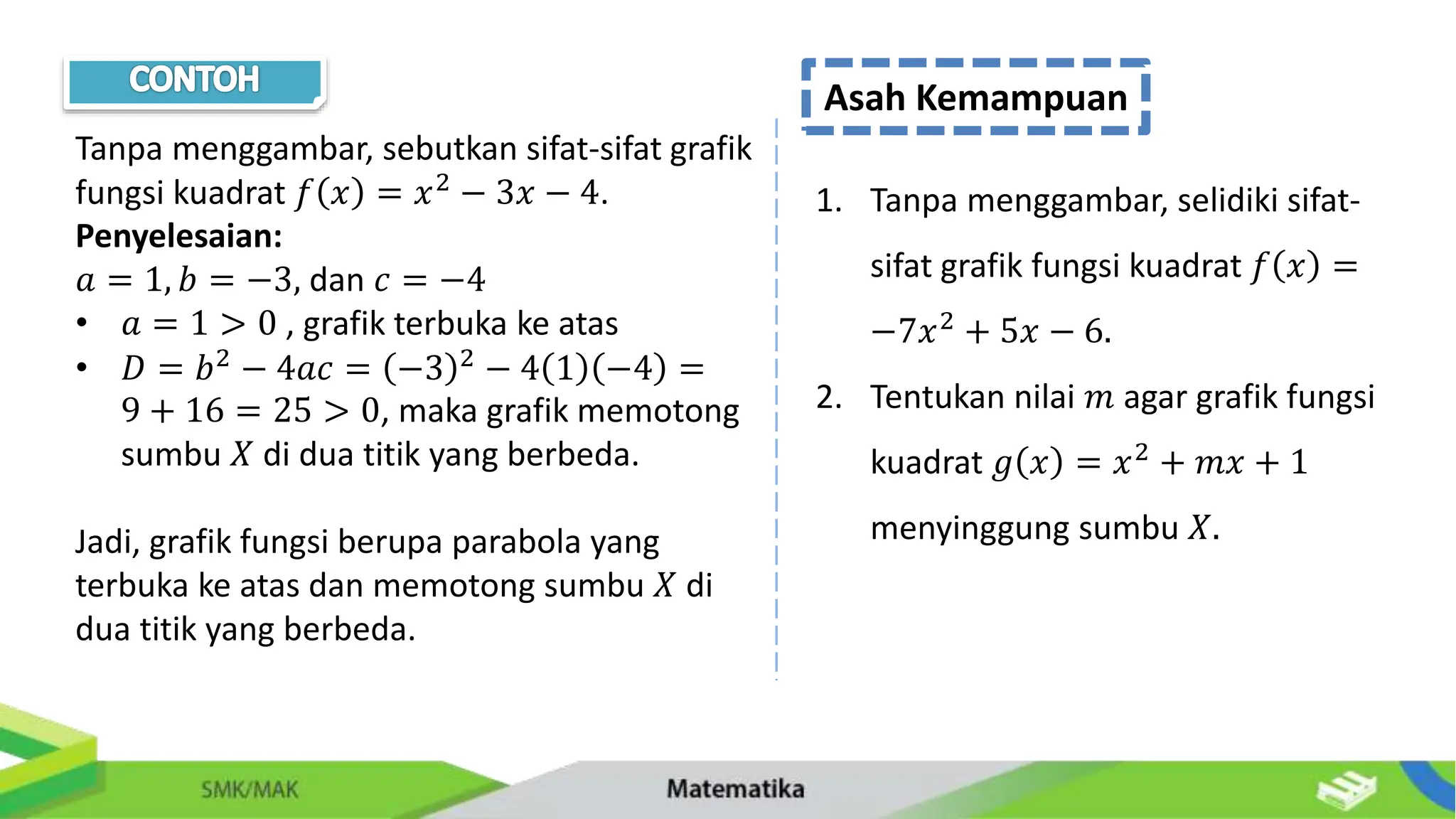
Dokumen ini membahas tentang persamaan dan fungsi kuadrat untuk siswa SMK/Mak kelas XI, mencakup definisi, cara menyelesaikan, dan aplikasi persamaan kuadrat. Terdapat penjelasan mendetail tentang faktorisasi, melengkapi bentuk kuadrat sempurna, serta penggunaan rumus ABC untuk mencari akar. Selain itu, juga diberikan contoh soal dan aplikasi kehidupan nyata yang melibatkan persamaan kuadrat.

1. Matematika
MEDIA MENGAJAR
UNTUK SMK/MAK KELAS XI

2. BAB 1
Persamaan dan Fungsi
Kuadrat
Sumber: flickr.com/©Bert
Kaufmann

3. Persamaan dan
Fungsi Kuadrat
Persamaan
Kuadrat
Faktorisasi
Kuadrat
Sempurna
Rumus
abc
Akar-akar
Persamaan
Kuadrat
Rumus Jumlah
dan Hasil Kali
Akar
Menyusun
Persamaan
Kuadrat
Aplikasi
Persamaan
Kuadrat
Fungsi
Kuadrat
Menggambar
Grafik
Sifat-sifat
Grafik Menerapkan
Fungsi
Kuadrat

4. A. PERSAMAAN KUADRAT
Persamaan kuadrat adalah persamaan dengan pangkat tertinggi variabelnya adalah dua.
𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄 = 𝟎 dengan 𝑎 ≠ 0, 𝑎, 𝑏, 𝑐 ∈ 𝑹
Bentuk Umum
• 2𝑥2 + 4𝑥 − 1 = 0; 𝑎 = 2, 𝑏 = 4, dan 𝑐 = −1
• 𝑥2
+ 3𝑥 = 0; 𝑎 = 1, 𝑏 = 3, dan 𝑐 =0
• 2𝑥2
− 9 = 0; 𝑎 = 1, 𝑏 = 0, dan 𝑐 = −9
Menyelesaikan persamaan
kuadrat dalam 𝑥 artinya
mencari nilai 𝒙 sehingga jika
disubstitusi ke persamaannya
akan bernilai benar.
Penyelesaian persamaan
kuadrat disebut akar-akar
persamaan kuadrat.

5. Menentukan Akar-akar
Persamaan Kuadrat
Faktorisasi
Carilah akar-akar persamaan kuadrat dari
3𝑥2 + 2𝑥 − 5 = 0 dengan faktorisasi.
Penyelesaian:
𝑎 = 3, 𝑏 = 2, dan 𝑐 = −5 ⟶ 𝑎 ∙ 𝑐 = −15
dan 𝑏 = 2
• Cari dua bilangan yang hasil kalinya
adalah −15 dan jumlahnya adalah 2.
Dua bilangan yang memenuhi adalah
− 3 dan 5.
Cara:
Cari dua bilangan (misal: 𝑥1 dan 𝑥2) yang
memenuhi syarat sebagai berikut.
• Hasil kalinya adalah sama dengan 𝑎𝑐
𝒙𝟏 ∙ 𝒙𝟐 = 𝒂 ∙ 𝒄
• Jumlahnya adalah sama dengan 𝑏
𝒙𝟏 + 𝒙𝟐 = 𝒃
• Faktorkan bentuk 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0
menjadi
(𝒂𝒙+𝒙𝟏)(𝒂𝒙+𝒙𝟐)
𝒂
= 𝟎

6. Menentukan Akar-akar
Persamaan Kuadrat
Faktorisasi
1
dan
3
5
adalah
kuadratnya
persamaan
akar
-
akar
Jadi,
1
3
5
3
3
5
3
0
3
3
atau
0
5
3
0
3
)
3
3
)(
5
3
(
0
5
2
3 2





















x
x
x
x
x
x
x
x
x
x
Cara:
Cari dua bilangan (misal: 𝑥1 dan 𝑥2) yang
memenuhi syarat sebagai berikut.
• Hasil kalinya adalah sama dengan 𝑎𝑐
𝒙𝟏 ∙ 𝒙𝟐 = 𝒂 ∙ 𝒄
• Jumlahnya adalah sama dengan 𝑏
𝒙𝟏 + 𝒙𝟐 = 𝒃
• Faktorkan bentuk 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0
menjadi
(𝒂𝒙+𝒙𝟏)(𝒂𝒙+𝒙𝟐)
𝒂
= 𝟎

7. Asah Kemampuan
1. Selesaikan persamaan kuadrat berikut dengan faktorisasi.
a. 𝑥2
− 7𝑥 + 6 = 0
b. 48 − 2𝑥 − 𝑥2 = 0
c. 𝑥2
− 9 = 0
d. 2𝑥2
+ 5𝑥 + 2 = 0
2. Fungsi 𝐻 𝑥 = 𝑥2
+ 𝑥 − 72 merupakan model keuntungan penjualan
sebanyak 𝑥 unit barang dari suatu perusahaan. Tentukan banyak barang
yang dijual jika perusahaan belum mendapatkan keuntungan.

8. Melengkapkan bentuk kuadrat sempurna
Cara:
• Pastikan koefisien 𝑥2 adalah 1. Jika
belum, bagi dengan bilangan yang
sesuai.
• Tambahkan ruas kiri dan kanan
dengan kuadrat dari setengah
koefisien 𝑥.
• Buat ruas kiri menjadi bentuk
kuadrat sempurna, sedangkan ruas
kanan disederhanakan.
Carilah akar-akar persamaan kuadrat dari
𝑥2
− 6𝑥 − 16 = 0 dengan melengkapkan
bentuk kuadrat sempurna.
Penyelesaian:
2
2
2
2
2
2
2
2
)
3
(
16
)
3
(
6
)
6
(
2
1
16
)
6
(
2
1
6
16
6
0
16
6


































x
x
x
x
x
x
x
x

9. Melengkapkan bentuk kuadrat sempurna
Cara:
• Pastikan koefisien 𝑥2 adalah 1. Jika
belum, bagi dengan bilangan yang
sesuai.
• Tambahkan ruas kiri dan kanan
dengan kuadrat dari setengah
koefisien 𝑥.
• Buat ruas kiri menjadi bentuk
kuadrat sempurna, sedangkan ruas
kanan disederhanakan.
Carilah akar-akar persamaan kuadrat dari
𝑥2
− 6𝑥 − 16 = 0 dengan melengkapkan
bentuk kuadrat sempurna.
Penyelesaian:
2
2
1 2
1 2
6 9 16 9
( 3) 25
3 5
5 3 atau 5 3
8 2
Jadi, akar-akar persamaan kuadratnya
adalah 2 dan 8.
x x
x
x
x x
x x
    
  
   
     
   


10. Asah Kemampuan
Selesaikan persamaan kuadrat
berikut dengan melengkapkan
bentuk kuadrat sempurna.
a. 𝑥2 − 5𝑥 − 24 = 0
b. 3 − 5𝑥 − 2𝑥2 = 0
c. 𝑥2 − 4 = 0
d. 9𝑥2 + 5𝑥 =2
Rumus 𝒂𝒃𝒄
Jika 𝑥1 dan 𝑥2 adalah akar-akar persamaan
kuadrat, maka:
a
ac
b
b
x
2
4
2
2
,
1





11. Carilah akar-akar persamaan
kuadrat dari 𝑥2 − 2𝑥 − 24 = 0
dengan melengkapkan bentuk
kuadrat sempurna.
Penyelesaian:
)
1
(
2
)
24
)(
1
(
4
)
2
(
)
2
(
2
4
24
dan
,
2
,
1
2
2
2
,
1
















a
ac
b
b
x
c
b
a
1 2
1 2
2 10 2 10
dan
2 2
6 4
Jadi, penyelesaiannya adalah 4 dan 6.
x x
x x
 
 
  

Asah Kemampuan
Selesaikan persamaan kuadrat berikut dengan
rumus 𝑎𝑏𝑐.
a. 𝑥2
+ 12𝑥 − 13 = 0
b. 3𝑥2
− 5𝑥 − 2 = 0
c. 2𝑥 + 5𝑥2
= 2

12. Jenis-jenis Akar Persamaan Kuadrat
Akar-akar persamaan akan bergantung pada nilai diskriminan (𝐷), dengan
𝑫 = 𝒃𝟐
− 𝟒𝒂𝒄
Nilai Diskriminan (𝑫) Jenis Akar Persamaan Kuadrat
𝐷 > 0 Mempunyai dua akar real yang berbeda
𝐷 = 0 Mempunyai dua akar real yang sama (akar
kembar)
𝐷 < 0 Mempunyai akar yang tidak real (imajiner)
Tabel hubungan nilai 𝐷 dengan jenis akar persamaan kuadrat

13. Selidiki jenis akar-akar persamaan
kuadrat dari 𝑥2 + 𝑥 + 3 = 0 tanpa
mencari akarnya terlebih dahulu.
Penyelesaian:
𝑎 = 1, 𝑏 = 1, dan 𝑐 = 3
𝐷 = 𝑏2 − 4𝑎𝑐
= 12 − 4 1 3
= 1 − 12
= −11
Karena 𝑫 < 𝟎, maka persamaan
kuadrat 𝑥2 + 𝑥 + 3 = 0 mempunyai
akar tidak real (imajiner).

14. Rumus Jumlah dan Hasil Kali Akar Persamaan Kuadrat
𝒙𝟏 + 𝒙𝟐 = −
𝒃
𝒂
𝒙𝟏𝒙𝟐 =
𝒄
𝒂
Jika 𝑥1 dan 𝑥2 adalah akar-akar persamaan
kuadrat 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0, maka: 1 2
2
2
2
2 2
2 1 2 1 2
2
Jika dan adalah akar-akar dari
persamaan kuadrat 4 1 0,
tentukan nilai .
1, 4, 1
( ) 2
( 4) 2( 1)
16 2 18
x x
x x
x x
a b c
x x x x x x
  

   
   
   
  
Penyelesaian :
2
1
2
1

15. Asah Kemampuan
1. Selidiki jenis akar-akar persamaan
kuadrat berikut.
a. 𝑥2 + 7𝑥 + 6 = 0
b. 4𝑥2 = 2𝑥 − 25
2. Jika 𝑥1 dan 𝑥2 merupakan akar-akar
persamaan kuadrat 𝑥2
+ 5𝑥 + 3 = 0,
tentukan nilai dari
2
𝑥1
+
2
𝑥2
.
3. Diketahui akar-akar persamaan
kuadrat 2𝑥2 + 𝑥 − 2 = 0 adalah 𝛼
dan 𝛽. Tentukan nilai dari 𝛼2
𝛽 + 𝛽2
𝛼.
4. Tentukan nilai 𝑝 agar persamaan 𝑥2
−
2𝑝𝑥 − 𝑝 + 2 = 0 mempunyai akar
kembar.

16. B. MENERAPKAN PERSAMAAN KUADRAT
Menyusun Persamaan Kuadrat yang Diketahui Akar-akarnya
Menggunakan rumus perkalian faktor
dan menyelesaikan persamaan
kuadrat dengan faktorisasi.
𝒙 − 𝒙𝟏 𝒙 − 𝒙𝟐 = 𝟎
Menggunakan rumus jumlah dan hasil
kali akar.
Jika 𝑥1 dan 𝑥2 adalah akar-akar persamaan kuadrat, maka untuk menyusun persamaan
kuadratnya adalah:
𝒙𝟐
− 𝒙𝟏 + 𝒙𝟐 𝒙 + 𝒙𝟏𝒙𝟐 = 𝟎

17. Tentukan persamaan kuadrat yang akar-
akarnya −8 dan 3.
Penyelesaian:
Misalkan 𝑥1 = −8 dan 𝑥2 = 3.
a. Cara I
Menggunakan rumus perkalian faktor,
Persamaan kuadratnya adalah:
𝑥 − 𝑥1 𝑥 − 𝑥2 = 0
⟺ 𝑥 − −8 𝑥 − 3 = 0
⟺ 𝑥 + 8 𝑥 − 3 = 0
⟺ 𝑥2
−3𝑥 + 8𝑥 − 24 = 0
⟺ 𝑥2
+5𝑥 − 24 = 0.
b. Cara II
Menggunakan rumus jumlah dan hasil kali
akar.
Persamaan kuadratnya adalah:
𝑥2 − 𝑥1 + 𝑥2 𝑥 + 𝑥1𝑥2 = 0
⟺ 𝑥2 − −5 𝑥 + −24 = 0
⟺ 𝑥2
+5𝑥 − 24 = 0.

18. Menyusun Persamaan Kuadrat Berdasarkan Akar-akar Persamaan Kuadrat Lain
Susunlah persamaan kuadrat yang akar-
akarnya lima lebihnya dari akar-akar
persamaan kuadrat 𝑥2 − 8𝑥 + 2 = 0.
Penyelesaian:
𝑎 = 1, 𝑏 = −8, dan 𝑐 = 2
𝑥1 + 𝑥2 = −
𝑏
𝑎
= −
−8
1
= 8 dan
𝑥1𝑥2 =
𝑐
𝑎
=
2
1
= 2
Misalkan akar-akar persamaan kuadrat baru
yang akan dicari adalah 𝛼 dan 𝛽, maka 𝛼 =
𝑥1 + 5 dan 𝛽 = 𝑥2 + 5.
𝛼 + β = 𝑥1 + 5 + (𝑥2+5)
= (𝑥1+𝑥2) + 10
= 8 + 10 = 18
𝛼β = 𝑥1 + 5 (𝑥2+5)
= 𝑥1𝑥2 + 5𝑥1 + 5𝑥2 + 5 5
= 𝑥1𝑥2 + 5(𝑥1 + 𝑥2) + 25
= 2 + 5 8 + 25 = 67
Jadi, persamaan kuadrat barunya adalah:
𝑥2 − 𝛼 + 𝛽 𝑥 + 𝛼𝛽 = 0
⟺ 𝑥2
−18𝑥 + 67 = 0.

19. Asah Kemampuan
1. Susun persamaan kuadrat yang mempunyai akar-akar −2 dan 5 dengan menggunakan
rumus perkalian faktor.
2. Susun persamaan kuadrat yang mempunyai akar-akar
2
5
dan 5 dengan menggunakan
rumus jumlah dan hasil kali akar.
3. Akar-akar persamaan kuadrat 3𝑥2 − 2𝑥 + 10 = 0 adalah 𝑥1 dan 𝑥2. Tentukan
persamaan kuadrat baru yang akar-akarnya 2𝑥1 + 1 dan 2𝑥2 + 1.
4. Diketahui persamaan kuadrat 𝑥2
− 4𝑥 + 2 = 0 mempunyai akar-akar 𝛼 dan 𝛽.
Tentukan persamaan kuadrat baru yang mempunyai akar-akar berkebalikan dengan
akar-akar kuadrat tersebut.

20. Aplikasi Persamaan Kuadrat
Sejumlah siswa patungan untuk membeli
alat praktikum seharga Rp612.000,00.
Setelah masing-masing membayar degan
jumlah yang sama, ada 3 temannya yang
ingin bergabung. Jika ketiga temannya
ikut bergabung, masing-masing akan
membayar Rp34.000,00 kurangnya dari
yang telah mereka bayar. Tentukan
jumlah siswa yang berencana akan
membeli alat praktikum tersebut.
Penyelesaian:
Misalkan jumlah siswa = 𝑥, maka
masing-masing siswa membayar sebesar =
612.000
𝑥
.
Setelah 3 temannya bergabung, masing-
masing siswa membayar =
612.000
𝑥+3
.
Selisih pembayaran = pembayaran mula-
mula − pembayaran setelah 3 temannya
bergabung

21. Aplikasi Persamaan Kuadrat Penyelesaian:
⟺ 34.000 =
612.000
𝑥
−
612.000
𝑥 + 3
⇔ 1 =
18
𝑥
−
18
𝑥 + 3
⇔ 𝑥 𝑥 + 3 = 18 𝑥 + 3 − 18𝑥
⇔ 𝑥2
+3𝑥 = 18𝑥 + 54 − 18𝑥
⇔ 𝑥2 + 3𝑥 − 54 = 0
⇔ 𝑥 + 9 𝑥 − 6 = 0
⇔ 𝑥 = −9 atau 𝑥 = 6
Jadi, sebelum 3 temannya bergabung ada
6 siswa yang akan patungan membeli alat
praktikum tersebut.
Sejumlah siswa patungan untuk membeli
alat praktikum seharga Rp612.000,00.
Setelah masing-masing membayar degan
jumlah yang sama, ada 3 temannya yang
ingin bergabung. Jika ketiga temannya
ikut bergabung, masing-masing akan
membayar Rp34.000,00 kurangnya dari
yang telah mereka bayar. Tentukan
jumlah siswa yang berencana akan
membeli alat praktikum tersebut.

22. Suatu fungsi dalam himpunan
bilangan yang dinyatakan dengan
rumus fungsi berikut.
C. FUNGSI KUADRAT
𝒇 𝒙 = 𝒂𝒙𝟐 + 𝒃𝒙 + 𝒄
dengana ≠ 0, dan a, b, c 𝜖 R
Untuk menggambar grafik fungsi kuadrat
pada koordinat Cartesius, lambang 𝑓(𝑥)
dapat diganti dengan 𝑦 sehingga 𝑓 𝑥 =
𝑎𝑥2
+ 𝑏𝑥 + 𝑐 dapat ditulis 𝑦 = 𝑎𝑥2
+
𝑏𝑥 + 𝑐, dengan 𝒙 disebut variabel bebas
dan 𝒚 disebut variabel terikat.
Grafik fungsi kuadrat berbentuk
parabola simetris.

23. Gambarkan grafik fungsi kuadrat
𝑦 = 𝑥2
− 4𝑥 − 5.
Penyelesaian:
• Tentukan titik potong dengan
sumbu X (𝑦 = 0)
𝑦 = 𝑥2 − 4𝑥 − 5
 𝑥 + 1 𝑥 − 5 = 0
𝑥 = −1 atau 𝑥 = 5
Titik potong: (−1,0) dan (5, 0).
• Tentukan titik potong dengan sumbu Y
(𝑥 = 0)
𝑦 = 𝑥2 − 4𝑥 − 5 ⇔ 𝑦 = −5
Titik potong: (0, −5)
• Tentukan sumbu simetri dari persamaan
dengan cara
𝑥 = −
𝑏
2𝑎
= −
−4
2 1
= 2
𝑦 = −
𝐷
4𝑎
= −
−4 2−4 1 −5
4 1
= −9
Sumbu simetrinya 𝑥 = 2 dan koordinat
titik baliknya (2, −9).
Menggambar Grafik Fungsi Kuadrat

24. Gambarkan grafik fungsi kuadrat 𝑦 =
𝑥2 − 4𝑥 − 5.
Penyelesaian:
• Tentukan beberapa titik bantu.
Misal 𝑥 = 1
𝑦 = 𝑥2 − 4𝑥 − 5
= 1 2 − 4 1 − 5 = −8
Titik bantu: 1, −8 .
Menggambar Grafik Fungsi Kuadrat
𝑂
𝑌
𝑋
−9
−5
−1
−8
1 2
Gambarkan grafiknya

25. Asah Kemampuan
1. Gambarlah sketsa grafik fungsi kuadrat
𝑔 𝑥 = −𝑥2
+ 𝑥 − 6.
2. Bayangan 𝑥 = −2 oleh fungsi 𝑓 𝑥 = 𝑥2
−
3𝑥 + 𝑘 − 1 adalah 0. Tentukan nilai 𝑘 dan
gambarkan grafiknya.
3. Nilai minimum fungsi 𝑓 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 − 8
adalah −9 dicapai pada 𝑥 = 1. Tentukan
nilai 𝑎 dan 𝑏 yang memenuhi kemudian
sketsa gambar grafiknya.
𝑎 > 0 𝑎 < 0
Grafik terbuka ke
atas
Grafik terbuka ke
bawah
Memiliki nilai
ekstrim minimum
(𝑦𝑚𝑖𝑛)
Memiliki nilai
ekstrim maksimum
(𝑦𝑚𝑎𝑘𝑠)
Bentuk grafik: Bentuk grafik:
Sifat-sifat Grafik Fungsi Kuadrat
Berdasarkan nilai 𝒂

26. Grafik Memotong Sumbu 𝑿
D > 0 D = 0 D < 0
Grafik
memotong
sumbu X di dua
titik berbeda
Grafik
memotong
sumbu X di
sebuah titik
Grafik tidak memotong dan tidak
menyinggung sumbu X
Bentuk
Grafik
𝑎 > 0
Definit positif
(bernilai positif
untuk seluruh nilai 𝑥)
Bentuk
Grafik
𝑎 < 0
Definit negatif
(bernilai negatif
untuk seluruh nilai 𝑥)
X X
Berdasarkan nilai diskriminan (𝑫 = 𝒃𝟐 − 𝟒𝒂𝒄)
X X
X
X

27. Tanpa menggambar, sebutkan sifat-sifat grafik
fungsi kuadrat 𝑓 𝑥 = 𝑥2
− 3𝑥 − 4.
Penyelesaian:
𝑎 = 1, 𝑏 = −3, dan 𝑐 = −4
• 𝑎 = 1 > 0 , grafik terbuka ke atas
• 𝐷 = 𝑏2 − 4𝑎𝑐 = −3 2 − 4 1 −4 =
9 + 16 = 25 > 0, maka grafik memotong
sumbu 𝑋 di dua titik yang berbeda.
Jadi, grafik fungsi berupa parabola yang
terbuka ke atas dan memotong sumbu 𝑋 di
dua titik yang berbeda.
Asah Kemampuan
1. Tanpa menggambar, selidiki sifat-
sifat grafik fungsi kuadrat 𝑓 𝑥 =
−7𝑥2
+ 5𝑥 − 6.
2. Tentukan nilai 𝑚 agar grafik fungsi
kuadrat 𝑔 𝑥 = 𝑥2 + 𝑚𝑥 + 1
menyinggung sumbu 𝑋.

28. Tentukan persamaan grafik fungsi kuadrat
yang melalui titik 1, −4 , 0, −3 , dan
4,5 .
Penyelesaian:
𝑓 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
𝑓 1 = 𝑎(1)2
+𝑏 1 + 𝑐 = −4
⇔ 𝑎 + 𝑏 + 𝑐 = −4 . . . (1)
𝑓 0 = 𝑎(0)2
+𝑏 0 + 𝑐 = −3
⇔ 𝑐 = −3 . . . (2)
𝑓(4) = 𝑎(4)2
+𝑏 4 + 𝑐 = 5
⇔ 16𝑎 + 4𝑏 + 𝑐 = 5 . . . (3)
Menerapkan Fungsi Kuadrat
Menentukan persamaan fungsi kuadrat 𝒇 𝒙 = 𝒂𝒙𝟐
+ 𝒃𝒙 + 𝒄 jika diketahui grafik
fungsi melalui tiga titik

29. Tentukan persamaan grafik fungsi kuadrat
yang melalui titik 1, −4 , 0, −3 , dan
4,5 .
Penyelesaian:
Substitusi persamaan (2) dan (1).
𝑎 + 𝑏 + 𝑐 = −4
 𝑎 + 𝑏 − 3 = −4 ⇔ 𝑎 + 𝑏 = −1 ... (4)
Substitusi persamaan (2) dan (3).
16𝑎 + 4𝑏 + 𝑐 = 5
 16𝑎 + 4𝑏 − 3 = 5
 16𝑎 + 4𝑏 = 8 . . . (5)
Menerapkan Fungsi Kuadrat
Menentukan persamaan grafik fungsi kuadrat 𝒇 𝒙 = 𝒂𝒙𝟐
+ 𝒃𝒙 + 𝒄 jika diketahui
grafik fungsi melalui tiga titik

30. Tentukan persamaan grafik fungsi kuadrat
yang melalui titik 1, −4 , 0, −3 , dan
4,5 .
Penyelesaian:
Eliminasi persamaan (4) dan (5).
Menerapkan Fungsi Kuadrat
Menentukan persamaan grafik fungsi kuadrat 𝒇 𝒙 = 𝒂𝒙𝟐
+ 𝒃𝒙 + 𝒄 jika diketahui
grafik fungsi melalui tiga titik
1| 4 | 4 4 4
16 4 8 | 1|16 4 8
12 12
1
a b a b
a b a b
a
a
      
     
  

Substitusi nilai 𝑎.
𝑎 + 𝑏 = −1
⇔ 1 + 𝑏 = −1
⇔ 𝑏 = −2
Jadi, fungsi kuadratnya adalah
𝒇 𝒙 = 𝒙𝟐
− 𝟐𝒙 − 𝟑.

31. Menerapkan Fungsi Kuadrat
Menentukan persamaan grafik fungsi kuadrat 𝒇 𝒙 = 𝒂𝒙𝟐
+ 𝒃𝒙 + 𝒄 jika diketahui
dua titik potong terhadap sumbu 𝑿 dan satu titik yang lainnya
𝒇 𝒙 = 𝒂(𝒙 − 𝒙𝟏)(𝒙 − 𝒙𝟐)
Tentukan persamaan grafik fungsi
kuadrat yang memotong sumbu X di
titik (1, 0) dan (−3,0) dan memotong
sumbu Y di titik (0, 3).
Penyelesaian:
𝑓 𝑥 = 𝑎(𝑥 − 𝑥1)(𝑥 − 𝑥2)
titik (1,0) dan (−3,0) disubstitusi ke
𝑓(𝑥)
𝑓 𝑥 = 𝑎(𝑥 − 1)(𝑥 + 3) . . . (1)
Substitusi titik (0, 3) ke (1).
𝑓 𝑥 = 𝑎(𝑥 − 1)(𝑥 + 3)
 3 = 𝑎 0 − 1 0 + 3
 3 = −3𝑎
 𝑎 = −1

32. Menerapkan Fungsi Kuadrat
Menentukan persamaan grafikfungsi kuadrat 𝒇 𝒙 = 𝒂𝒙𝟐
+ 𝒃𝒙 + 𝒄 jika diketahui
dua titik potong terhadap sumbu 𝑿 dan satu titik yang lainnya
𝒇 𝒙 = 𝒂(𝒙 − 𝒙𝟏)(𝒙 − 𝒙𝟐)
Tentukan persamaan grafik fungsi
kuadrat yang memotong sumbu X di
titik (1, 0) dan (−3, 0) dan memotong
sumbu Y di titik (0, 3).
Penyelesaian:
Persamaan fungsi kuadratnya
𝑓 𝑥 = 𝑎 𝑥 − 1 𝑥 + 3
𝑓 𝑥 = −1(𝑥 − 1)(𝑥 + 3)
 𝑓 𝑥 = −1 𝑥2
+ 2𝑥 − 3
 𝑓 𝑥 = −𝑥2
− 2𝑥 + 3
Jadi, persamaan grafik fungsi
kuadratnya:
𝒇 𝒙 = −𝒙𝟐
− 𝟐𝒙 + 𝟑.

33. Menerapkan Fungsi Kuadrat
Menentukan persamaan grafik fungsi kuadrat 𝒇 𝒙 = 𝒂𝒙𝟐
+ 𝒃𝒙 + 𝒄 jika diketahui
titik puncak grafik (𝒙𝒑, 𝒚𝒑) dan satu titik lainnya
𝒇 𝒙 = 𝒂(𝒙 − 𝒙𝒑)𝟐+𝒚𝒑
Substitusi titik 3, −7 ke (1).
𝑓 𝑥 = 𝑎(𝑥 + 1)2
+9
 −7 = 𝑎(3 + 1)2+9
 −16 = 16𝑎
 𝑎 = −1
Tentukan persamaan grafik fungsi
kuadrat yang memiliki titik puncak
−1,9 dan melalui titik 3, −7 .
Penyelesaian:
𝑓 𝑥 = 𝑎(𝑥 − 𝑥𝑝)2+𝑦𝑝
 𝑓 𝑥 = 𝑎(𝑥 + 1)2
+9 . . .(1)

34. Menerapkan Fungsi Kuadrat
Menentukan persamaan grafik fungsi kuadrat 𝒇 𝒙 = 𝒂𝒙𝟐
+ 𝒃𝒙 + 𝒄 jika diketahui
titik puncak grafik (𝒙𝒑, 𝒚𝒑) dan satu titik lainnya.
𝒇 𝒙 = 𝒂(𝒙 − 𝒙𝒑)𝟐+𝒚𝒑
 𝑓 𝑥 = −1(𝑥 + 1)2
+9
 𝑓(𝑥) = −1(𝑥2
+2𝑥 + 1) + 9
 𝑓 𝑥 = −𝑥2
− 2𝑥 − 1 + 9
 𝑓 𝑥 = −𝑥2
− 2𝑥 + 8
Jadi, persamaan kuadratnya:
𝒇 𝒙 = −𝒙𝟐
− 𝟐𝒙 + 𝟖.
Tentukan persamaan grafik fungsi
kuadrat yang memiliki titik puncak
−1,9 dan melalui titik 3, −7 .
Penyelesaian:
Substitusi nilai 𝑎.
𝑓 𝑥 = 𝑎(𝑥 + 1)2
+9

35. Lintasan sebuah peluru
yang ditembakkan vertikal
ke atas setinggi ℎ meter
dalam waktu 𝑡 detik
dinyatakan dengan rumus
ℎ = 40𝑡 − 5𝑡2
. Tentukan:
a. waktu yang
diperlukan untuk
mencapat tinggi
maksimum dan
b. tinggi maksimum
peluru.
Penyelesaian:
ℎ = 40𝑡 − 5𝑡2
a. Tinggi maksimum dicapai pada
𝑡 = −
𝑏
2𝑎
= −
40
2 −5
= 4
Jadi, waktu yang diperlukan adalah 4 detik.
b. ℎ𝑚𝑎𝑘𝑠= −
𝐷
4𝑎
= −
402−4 −5 0
4 −5
= 80
Jadi, tinggi maksimum adalah 80 meter.
Penerapan Fungsi Kuadrat

36. 1. Sebuah kembang api diluncurkan ke udara. Ketinggian kembang api pada saat 𝑡 detik
adalah ℎ meter yang didefinisikan dengan rumus ℎ 𝑡 = −16𝑡2 + 200𝑡 + 4. Kapan
kembang api tersebut mencapai tinggi maksimum dan berapa tinggi maksimum
kembang api tersebut?
2. Tentukan persamaan fungsi kuadrat yang melalui:
a. titik 1, −15 , 0, −8 , dan (−1,5),
b. titik 6,0 , 2,0 , dan 1,5 , serta
c. titik (4,5) dan titik puncaknya (−2,1).
Asah Kemampuan