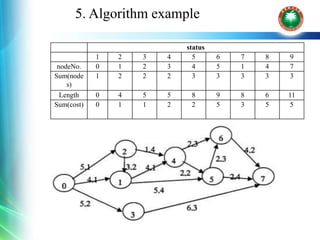
This document presents an algorithm for finding restricted shortest paths in a graph. 1. The algorithm uses breadth-first search to find paths from a source node to a target node that satisfy restrictions on path length and cost. It prunes paths that do not meet the restrictions to reduce the search space. 2. It uses adjacency lists and a shortest path tree data structure to store graph information and explored paths. A queue holds paths to explore at each level of the search. 3. The algorithm initializes data structures and the starting node, then iterates exploring neighbors of the current path until it finds a path from source to target within the restrictions or exhausts all such paths.

1. Title:- An Algorithm For Restricted Shortest Path
Search
BIT. School of Computer Science and Technology.
April , 2019,
Name. HABIB FIGA
ID. 3820181124

2. 1. Problem Definition
2. Main idea
3. Data Structure
4. Process of Algorithm
5. Example
6. Time Complexity
Content

3. 1. Problem Definition
1. Definition 1. Let G=(V;E) be a graph with |V|=n and |E|=m, such that
each edge e∈E is associated with several weights (can called cost, length,
delay, .etc). And give some positive integer to make path Restriction.
2. Restricted shortest path problem is to find a path p in G from s to t such
that sum of some weights satisfied some Restriction and the length of p is
minimal.
3. In my example, there are two weights named length and cost, the
problem is to find the shortest path with cost no greater than 8 and nodes
in path less than 4.

4. 5.Example
Algorithm example
Figure 1.
The first coefficient on each side in figure 1, is the path length
and the second coefficient is Cost.
Set the source point S-0 the end point 1-7, the number of vertex
K-4,and cost limit 1-8 ,and use this algorithm to find all the
Shortest paths from the source node 0 to the end point 7 when the
number of vertex limit is 4 and cost limit is 8.

5. 2.Main idea
A. BFS(Breadth First Search)
 Explores all of the neighbor nodes at the present depth prior to
moving on to the nodes at the next depth level.
 It uses the opposite strategy as depth first search, which instead
explores the highest-depth nodes first before being forced to backtrack
and expand shallower nodes.
A. Pruning
 Reduce the search for paths won’t satisfied the Restriction.

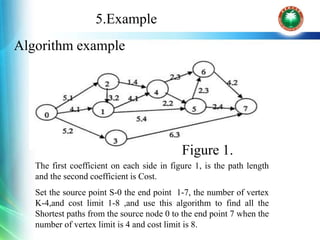
6. 3.Data structure
 Adjacency List
typedef struct QNode{
int q; //the next node
int length; //the length from n to q
int cost; //the cost from n to q
struct Node * link; //points to another node which the node n can go to
}Node;
Node *hg [n];

7. Adjacency List of Fig 2.
3.Data structure
Figure 1.

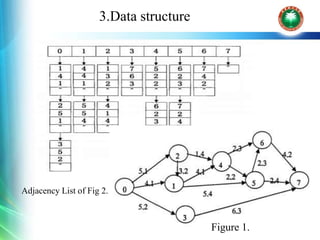
8.  Shortest Tath Tree
typedef struct Anode {
int data; //the last node in current path
int length; //length of current path
int cost; //cost of current path
int distance; // nodes in current path
struct ANode * Parent; //point to the previous node
}ANode;
Anode* a[];
 A Queue to store path to the current node
3.Data structure

9. The Shortest path tree of Fig 3.
3.Data structure

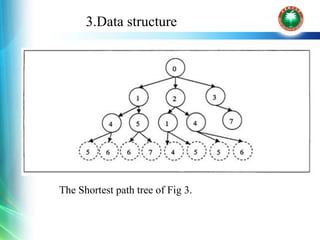
10. 4.Algorithm process
Initialization
Given K as Nodes limitation, L as Cost limitation
int u = ∞ // u is a positive value that is much larger than the possible path length
int flag = 0 //flag notes whether we find a path satisfied the Restriction
Anode *a[]
The Source node s(s->data = 0, s->distance = 1)
Queue.push(s);
Target node n;

11. 1. While:
2. if Queue.head->distance < K(4): // judge the nodes of current path
3. p = Queue.pop()
4. if p->cost < L(8): // judge the sum of cost of current path
5. if p->data == n: //judge is a path from source to target
6. if p->length < u: u = p->length, flag = 1
7. add p into the Array A
8. else: i = p->data
9. for q in hg[i]:
10. add value from q to p as new path
11. add new path in to Queue
12. else:
13. continue
14. else:
15. break
4.Algorithm process
Adjacency List “q(hg)” Fig 2.

12. Get result
if flag == 1:
u is the Restricted Shortest path
find the path from the Shortest path tree
else:
no path satisfied the Restriction
4.Algorithm process

15. An array of pointer with length n list is an adjacent list I point to a list and each
element in the list is the adjacency point of vertex V.
Data is the current shortest path length from data node to the end point
The first element of queue ,is out of the queue to determine whether the shortest
path length to the destination exist in the cost domain of the node “adjacent to out
going node.
Explanation

16. status
1 2 3 4 5 6 7 8 9
nodeNo. 0 1 2 3 4 5 1 4 7
Sum(node
s)
1 2 2 2 3 3 3 3 3
Length 0 4 5 5 8 9 8 6 11
Sum(cost) 0 1 1 2 2 5 3 5 5
5. Algorithm example

17. 6.Time Complexity
O(k*n*sh2(G,k,l))
k – the nodes Restriction
n – the count of nodes in the graph
sh2(G,k,l) – the count of paths satisfied the Restriction of
nodes(k) and cost(L) in graph G

18. Thank You!
An Algorithm for Restricted Shortest Path Search