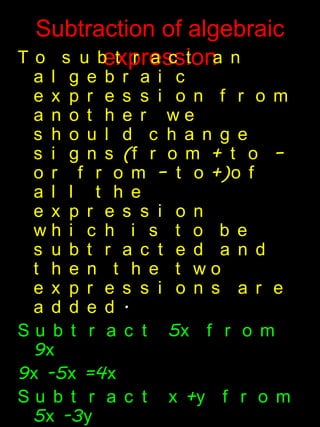
An algebraic expression is a combination of constants and variables connected by fundamental operations. It contains terms which are separated by addition or subtraction signs. There are different types of algebraic expressions based on the number of terms: monomial (one term), binomial (two terms), trinomial (three terms), and polynomials (two or more terms). Factors are the numbers and variables that make up each term. Like terms contain the same literal factors, while unlike terms do not. To add or subtract algebraic expressions, like terms are collected and their coefficients are combined.

1. Algebraic Expressions

2. Algebraic expressionA Combination of constants and variables connected by the signs of fundamental operations of addition,subtraction, division and multiplication is called an algebraic expression. Terms Various parts of an algebraic expression which are seprated by the signs+ or – are called the ‘terms’ of the expression.Illustration-3y+4x is an algebraic expressions having 3y and 4x as terms

3. Types of Algebraic expressionsMonomial- an algebraic expression containing only one term Example-3x , 4z, 2y ,5t are monomials.Binomial-An algebraic expression containing two terms.Example-3y+5x , 4z-6y , 2x+6x are binomials.Trinomial-An algebraic expression containing three terms.Example-3x+4z-2w , 5y+4z-3x, 4z-1y+10x are trinomials.Quadrinomial-An algebraic expression containing four terms.Example-3y+x+6y-7x , 4z+5z-6x+10x are quadrinomials.

4. PolynomialAn algebraic expression two or more terms is called a polynomial.FactorsEach term in an algebraic expression is a product of one or more number[s] and/ or literal number(s).These number(s) are known as the factors of that term. Illustration- The monomial 7x is the product of the number 7 and literal x. So 7 and x are the factors of monomial 7x .

5. In the term -4xyz , the numerical factor is -4 and x, y , z are literal factors.

6. In he binomial expression xy+3 , the term xy has 1 as its numerical factor while x and y are literal factors. The term 3 has only numerical factor. It has no literal factor. Constant termA Term of the expression having no literal factor is called a constant termIllustration-In the binomial expression 5x + 7 ,the constant term is 7. COEFFICIENT In a term of an algebraic expression, any of the factors with the sign of the term is called the coefficient of the product of the other factors.Illustration-In the monomial 3xy,the coefficient of xy is 3,the coefficient of x is 3y, the coefficient of y is 3x.

7. Consider the term -8xy in the binomial -8xy+7.The coefficient of x is the term -8xy is -8y the coefficient of y is -8x and the coefficient of xy is -8Like TermsThe terms having the same literal factors are called like or similar termsUnlike termsThe terms not having same literal factors are called unlike or dissimilar terms.Illustration- In the algebraic expression 5xy+8xy -3yz-9yc, we have 5xy and 8xyas like terms, whereas -3yz and -9yc are unlike terms.In the expression 16x,16y we have 16x and 16y as unlike terms because the literal factors x and y are not same.

8. Addition of negative like terms.Step1-Obtain all like terms.Step2-Obtain the sum of the numerical coefficients (without the negative sign) of all like terms.Step3-Write an expression as a product of the number obtained is step2, with all the literal coefficients preceded by a minus sign.Step4-The expression obtained in step3 is the required sum.Add -7xy,-3xy,-9xyThe sum of the numerical coefficients(without the negative sign) is7+3+9=19 Hence -7x,-3xy,-9xy=-19xy

9. Operations On Algebraic Expression.Addition of positive termsProcedure- Obtain all like terms.Find the sum of the numerical coefficients of all like terms.Write the required sum as a like term whose numerical coefficients is the numerical obtained in step 2 and literal factors of the given like terms.Illustration-Add 4xy ,12xy and 3xySolution- The sum of the numerical coefficients of the given like terms is 4+12+3=19.Thus the sum of the given like terms is another like term whose numerical coefficient is 19.Hence,4xy+12xy+3xy=19xy.Aliter-the sum of the given like terms can also be obtained by using the distributive property of multiplication over addition as discussed below-4xy+12xy+3xy=(4+12+3)xy=19xy

10. Addition of +ive and –ive like termsStep1-Collect all +ive like terms and find their sum.Step2-Collect all the -ive like terms and find their sum.Step3-Obtain the numerical coefficients(without -ive sign) of like terms obtained in steps1 and 2.Step4-Subtract the numerical coefficient in step2 from the numerical coefficient in steop1.Write the answer as a product of this number and all the literal coefficients.Add 4xy,8xy,-2xy4xy+8xy- 2xy(4xy+8xy)-2xy (Collecting +ive and –ive like terms together) 12xy-2xy=10xy

11. Addition of algebraic expression with an unlike terms likeIn adding algebraic expression containing like and unlike terms we collect different groups of like terms and find the sum of like terms in each groups by the methods discussed below-1)Horizontal method 2)Column method(7x+4)+(3x-1) 7x+4 =(7x+3x)+(4-1) +3x-1 =10x+3 =10x+3