AIOU Solved Assignment Code 1349 Introduction To Business Mathematics Autumn 2023 Assignment 2.pdf

ALLAMA IQBAL OPEN UNIVERSITY ISLAMABAD
(Department of Mathematics)
Course: Introduction to Business Mathematics (1349)
Semester: Autumn, 2023
Level: HSSC
ASSIGNMENT No. 2
Q.1 (a) Six years ago the age of a mother was 3 times the age of her
daughter. It will be twice after 9 years. Find their present ages.
Let's call the current age of the mother M and the current age of the daughter
D. We're given two pieces of information:
0314-4646739 0332-4646739 03364646739
Skilling.pk Diya.pk Stamflay.com

Six years ago, the age of the mother was 3 times the age of her daughter, which
can be represented as:
M - 6 = 3(D - 6)
It will be twice after 9 years, which can be represented as:
M + 9 = 2(D + 9)
Now, let's solve this system of equations step by step.
Step 1:
Expand and simplify the first equation:
M - 6 = 3D - 18
0314-4646739 0332-4646739 03364646739

Step 2:
Add 6 to both sides of the equation to isolate M:
M = 3D - 18 + 6
M = 3D - 12
Step 3:
Now, we have an expression for M in terms of D. We can substitute this
expression into the second equation:
(3D - 12) + 9 = 2(D + 9)
0314-4646739 0332-4646739 03364646739

Step 4:
Now, let's solve for D:
3D - 3 = 2D + 18
Step 5:
Subtract 2D from both sides to isolate the D term:
D - 3 = 18
Step 6:
Add 3 to both sides to solve for D:
D = 18 + 3
0314-4646739 0332-4646739 03364646739

D = 21
Step 7:
Now that we know the daughter's age, we can find the mother's age using the
expression we found for M in step 2:
M = 3D - 12
M = 3(21) - 12
M = 63 - 12
M = 51
So, the daughter is currently 21 years old, and the mother is currently 51 years
old.
0314-4646739 0332-4646739 03364646739

(b) Find two numbers whose sum and product are 20 and 45 respectively.
Let's call the two numbers x and y. We're given two pieces of information:
The sum of the two numbers is 20, which can be represented as:
x + y = 20
The product of the two numbers is 45, which can be represented as:
xy = 45
0314-4646739 0332-4646739 03364646739

Step 1:
Solve the first equation for one of the variables. Let's solve for y:
y = 20 - x
Step 2:
Now, substitute this expression for y into the second equation:
x(20 - x) = 45
Step 3:
Expand and simplify the equation:
20x - x^2 = 45
0314-4646739 0332-4646739 03364646739

Step 4:
Rearrange the equation to get it in standard quadratic form (ax^2 + bx + c =
0):
x^2 - 20x + 45 = 0
Step 5:
Now, we need to solve this quadratic equation. You can use the quadratic
formula, which is:
x = (-b ± √(b² - 4ac)) / (2a)
0314-4646739 0332-4646739 03364646739

In this case, a = 1, b = -20, and c = 45. Plug these values into the formula:
x = (-(-20) ± √((-20)² - 4(1)(45))) / (2(1))
x = (20 ± √(400 - 180)) / 2
x = (20 ± √220) / 2
Step 6:
Now, simplify further:
x = (20 ± 2√55) / 2
Step 7:
Divide both the numerator and denominator by 2 to simplify:
0314-4646739 0332-4646739 03364646739

x = 10 ± √55
So, we have two possible values for x:
x = 10 + √55
x = 10 - √55
Now, you can find the corresponding values of y using the equation y = 20 -
x for each value of x.
Q.2 (a) Define any two relations on the set E = {2,4,6,8,10}.
Let's define two relations on the set E = {2, 4, 6, 8, 10):
0314-4646739 0332-4646739 03364646739

Equality Relation (R1):
This relation, denoted as R1, relates elements in E based on whether they are
equal. In this relation, two elements are related if and only if they are equal.
Mathematically, the equality relation R1 can be defined as:
R1 = {(a, b) | a, b ∈ E, and a = b}
In simpler terms, R1 contains pairs of elements from E where the elements
are equal. For example:
R1 = {(2, 2), (4, 4), (6, 6), (8, 8), (10, 10)}
0314-4646739 0332-4646739 03364646739

Divisibility Relation (R2):
This relation, denoted as R2, relates elements in E based on whether one
element is divisible by the other. In this relation, two elements are related if
one is a divisor of the other.
Mathematically, the divisibility relation R2 can be defined as:
R2 = {(a, b) | a, b ∈ E, and a divides b (a is a divisor of b)}
In simpler terms, R2 contains pairs of elements from E where one element
divides the other. For example:
R2 = {(2, 4), (2, 6), (2, 8), (2, 10), (4, 8), (4, 10), (6, 10)}
0314-4646739 0332-4646739 03364646739

In these relations, R1 captures the pairs of elements that are equal, and R2
captures the pairs of elements where one number is a divisor of the other
within the set E = {2, 4, 6, 8, 10}.
(b) Let the set M be given by M = {1,2,3,4,5} a relation S on the set M is
defined by, an S b if their sum a + b is an even number. Then find all the
elements that satisfy this relation.
To find all the elements that satisfy the relation S on the set M = {1, 2, 3, 4,
5}, where a relation S is defined by "a S b if their sum a + b is an even number,"
we need to determine all pairs (a, b) for which a + b is even.
0314-4646739 0332-4646739 03364646739

Step 1: Find all pairs (a, b) that satisfy the relation S.
We will go through the elements of set M and determine which pairs (a, b)
satisfy the relation S.
For a = 1:
If a + b is even, then b must be even. So, for a = 1, the pairs that satisfy the
relation S are (1, 2), (1, 4).
For a = 2:
If a + b is even, then b can be either even or odd. So, for a = 2, the pairs that
satisfy the relation S are (2, 1), (2, 3), (2, 5), (2, 2), (2, 4).
For a = 3:
0314-4646739 0332-4646739 03364646739

For a = 4:
If a + b is even, then b can be either even or odd. So, for a = 4, the pairs that
satisfy the relation S are (4, 1), (4, 3), (4, 5), (4, 2), (4, 4).
For a = 5:
Step 2: Compile all pairs (a, b) that satisfy the relation S.
The pairs (a, b) that satisfy the relation S are:
0314-4646739 0332-4646739 03364646739

(1, 2), (1, 4), (2, 1), (2, 3), (2, 5), (2, 2), (2, 4), (3, 2), (3, 4), (4, 1), (4, 3), (4,
5), (4, 2), (4, 4), (5, 2), (5, 4).
These are all the pairs of elements from the set M = {1, 2, 3, 4, 5} that satisfy
the relation S, where a S b if a + b is an even number.
Q.3 (a) Find the inverse of α if A is singular:
A = [𝟖
𝟓 𝟏 𝟐 𝟎
𝟐 𝟓 𝟏
𝟑 𝟐 𝟎 𝟏
𝟐 𝜶 −𝟏 𝟑
]
Step 1: Calculate the determinant of matrix A.
0314-4646739 0332-4646739 03364646739

You can calculate the determinant of a 4x4 matrix using expansion by minors
or other methods. In this case, let's use the method of cofactor expansion along
the top row:
Det(A) = 5 X Cofactor(1,1) - 1 X Cofactor(1,2) + 2 X Cofactor(1,3) - 0 X
Cofactor(1,4)
Now, let's calculate the cofactors for these submatrices:
Cofactor(1,1) = Det(| 2 5 1 |
| 2 0 1 |
0314-4646739 0332-4646739 03364646739

| α -1 3 |)
= 2(03 - 11) - 5(23 - 1α) + 1(2α - 52)
= 2(-1) - 5(6 - α) + (2α - 10)
= -2 - 30 + 2α + 10
= -32 + 2α
Cofactor(1,2) = Det(| 8 5 1 |
| 3 0 1 |
| 2 -1 3 |)
= 8(03 - 11) - 5(33 - 12) + 1(3X(-1) - 2X0)
= 8(-1) - 5(9 - 2) + 1(-3)
0314-4646739 0332-4646739 03364646739

= -8 - 35 - 3
= -46
Cofactor(1,3) = Det(| 8 2 1 |
| 3 2 1 |
| 2 α 3 |)
= 8(23 - 1α) - 2(33 - 12) + 1(3α - 22)
= 8(6 - α) - 2(9 - 2) + (3α - 4)
= 48 - 8α - 18 + 4 + 3α - 4
= 22 - 5α
0314-4646739 0332-4646739 03364646739

Cofactor (1,4) = Det(| 8 2 5 |
| 3 2 0 |
| 2 α -1 |)
= 8(20 - 5α) - 2(30 - 22) + 5(3α - 2(-1))
= 8(-5α) - 2(4) + 5(3α + 2)
= -40α - 8 + 15α + 10
= -25α + 2
Now, calculate Det(A):
Det(A) = 5(Cofactor(1,1))
0(Cofactor(1,4))
- (Cofactor(1,2)) + 2(Cofactor(1,3)) -
0314-4646739 0332-4646739 03364646739

Det(A) = 5(-32 + 2α) + 46 - 2(22 - 5α)
Det(A) = -160 + 10α + 46 - 44 + 10α
Det(A) = -158 + 20α
Step 2: Check if the determinant is zero.
If Det(A) = 0, then the matrix A is singular, and it doesn't have an inverse.
Therefore, for A to be singular:
-158 + 20α = 0
Solve for α:
0314-4646739 0332-4646739 03364646739

20α = 158
α = 158/20
α = 7.9
So, for α = 7.9, the matrix A is singular and doesn't have an inverse.
If you want to find the inverse of A for a specific value of α, you would need
to substitute that value into the matrix and then calculate the inverse using
various methods like Gaussian elimination or matrix algebra. However, for α
= 7.9, A is singular, and there is no unique inverse.
(b) Use matrices to solve the given system of linear equations:
2x + y + 3z = 3
0314-4646739 0332-4646739 03364646739

x + y – 2z = 0
-3x – y + 2z = 2
To solve the system of linear equations using matrices, you can represent the
system in matrix form Ax = b, where A is the coefficient matrix, x is the
column matrix of variables, and b is the column matrix of constants.
Here's the given system of equations:
2x + y + 3z = 3
x + y - 2z = 0
0314-4646739 0332-4646739 03364646739

-3x - y + 2z = 2
Let's represent this system in matrix form:
A X x = b
Where A is the coefficient matrix:
x is the column matrix of variables:
0314-4646739 0332-4646739 03364646739

And b is the column matrix of constants:
Now, to solve for x, you can use the matrix equation:
A X x = b
0314-4646739 0332-4646739 03364646739

Step 1: Find the inverse of matrix A.
Let's call the inverse of A as A^(-1). If A is invertible, then you can solve for
x using x = A^(-1) X b.
Step 2: Multiply both sides by A^(-1):
x = A^(-1) X b
Now, we need to find the inverse of matrix A.
Step 3: Calculate the inverse of A.
0314-4646739 0332-4646739 03364646739

det(A) = 2(12 - (-2)(-1)) - 1(12 - (-2)(-3)) + 3(1X(-1) - 1X(-3))
det(A) = 2(2 - 2) - 1(2 - 6) + 3(-1 + 3)
det(A) = 0 + 4 + 6
det(A) = 10
Now, calculate the entries of the inverse of A:
A^(-1) = (1/det(A)) X | (ei - fh) (ch - bi) (bf - ce) |
| (fg - di) (ai - cg) (cd - af) |
| (dh - eg) (bg - ah) (ae - bd) |
A^(-1) = (1/10) X | ((12 - (-2)(-1)) (-2X(-1) - 31) (3(-2) - 1X(-3)) |
| ((-32 - 2(-3)) (22 - (-3)(-3)) (1X(-3) - (-2)(-3)) |
0314-4646739 0332-4646739 03364646739

| ((-31 - 1X(-2)) (-12 - (-2)1) (2(-2) - (-3)(-3)) |
A^(-1) = (1/10) X | (2 - 2) (-2 + 3) (-6 + 3) |
| (-6 + 6) (4 - 9) (-3 + 6) |
| (-3 + 2) (-2 + 2) (-4 + 9) |
A^(-1) = (1/10) X | 0 1 -3 |
| 0 -5 3 |
| -1 0 5 |
Now, you have the inverse matrix A^(-1). Let's use it to solve for x.
Step 4: Multiply A^(-1) by b to find x:
0314-4646739 0332-4646739 03364646739

x = A^(-1) X b
x = (1/10) X | 0 1 -3 | X | 3 |
| 0 -5 3 | | 0 |
| -1 0 5 | | 2 |
Now, perform the matrix multiplication:
x = (1/10) X | (03 + 10 + (-3)(-1)) |
| (03 + (-5)0 + 32) |
| ((-1)3 + 00 + 5X2) |
x = (1/10) X | (0 + 0 + 3) |
0314-4646739 0332-4646739 03364646739

| (0 + 0 + 6) |
| (-3 + 0 + 10) |
x = (1/10) X | 3 |
| 6 |
| 7 |
Now, multiply each entry by (1/10):
x = | 3/10 |
| 6/10 |
| 7/10 |
0314-4646739 0332-4646739 03364646739

Simplify the fractions:
x = | 3/10 |
| 3/5 |
| 7/10 |
So, the solution to the system of equations is:
x = 3/10
y = 3/5
z = 7/10
0314-4646739 0332-4646739 03364646739

Q.4 (a) Nine pencils and five erasers cost Rs.60 and three pencils and ten
erasers cost Rs.45. Find the cost of one pencil and one eraser.
Let's denote the cost of one pencil as "P" (in rupees) and the cost of one eraser
as "E" (in rupees). We are given two pieces of information:
Nine pencils and five erasers cost Rs. 60, which can be represented as:
9P + 5E = 60
Three pencils and ten erasers cost Rs. 45, which can be represented as:
3P + 10E = 45
0314-4646739 0332-4646739 03364646739

Step 1: We can use the method of substitution or elimination to solve this
system of equations. Let's use the elimination method. Multiply the first
equation by 2 and the second equation by -3 to make the coefficients of "P" in
both equations cancel out when summed:
First equation: 2(9P + 5E) = 2(60) --> 18P + 10E = 120
Second equation: -3(3P + 10E) = -3(45) --> -9P - 30E = -135
0314-4646739 0332-4646739 03364646739

Now, add the modified equations together to eliminate "P":
(18P + 10E) + (-9P - 30E) = 120 - 135
Step 2: Simplify the equation:
18P - 9P + 10E - 30E = -15
9P - 20E = -15
Step 3: Solve for "P" in terms of "E":
9P = 20E - 15
P = (20E - 15)/9
0314-4646739 0332-4646739 03364646739

Step 4: Now, substitute this expression for "P" into one of the original
equations to solve for "E." Let's use the first equation:
9P + 5E = 60
9[(20E - 15)/9] + 5E = 60
Simplify the equation:
20E - 15 + 5E = 60
Step 5: Combine like terms and solve for "E":
25E - 15 = 60
0314-4646739 0332-4646739 03364646739

Add 15 to both sides:
25E = 60 + 15
25E = 75
Now, divide by 25 to find the cost of one eraser, "E":
E = 75/25
E = 3
So, the cost of one eraser is Rs. 3.
0314-4646739 0332-4646739 03364646739

Step 6: Now that we have the cost of one eraser, we can find the cost of one
pencil using the expression we derived in Step 3:
P = (20E - 15)/9
P = (20 X 3 - 15)/9
P = (60 - 15)/9
P = 45/9
P = 5
So, the cost of one pencil is Rs. 5.
Therefore, one pencil costs Rs. 5, and one eraser costs Rs. 3.
0314-4646739 0332-4646739 03364646739

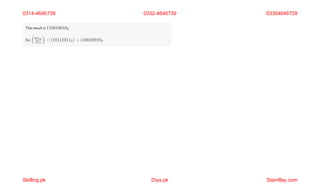
(b) Find the value of x if [𝟐 𝟏
𝟑 𝒙
] is singular.
0314-4646739 0332-4646739 03364646739

Q. 5 (a) Convert the following decimal systems into binary system:
(i) 67321 (ii) 143
0314-4646739 0332-4646739 03364646739

To convert decimal numbers into binary, you can use the process of successive
division by 2. Here's how you can convert the decimal numbers 67321 and
143 into binary step by step:
(i) Convert 67321 into binary:
Step 1: Start with the decimal number (67321).
Step 2: Divide the number by 2, and write down the quotient and the
remainder.
67321 ÷ 2 = 33660 remainder 1
0314-4646739 0332-4646739 03364646739

Step 3: Take the quotient from the previous step and repeat the process,
dividing it by 2 and recording the quotient and remainder.
33660 ÷ 2 = 16830 remainder 0
Step 4: Continue this process until the quotient becomes 0.
16830 ÷ 2 = 8415 remainder 0
8415 ÷ 2 = 4207 remainder 1
4207 ÷ 2 = 2103 remainder 1
2103 ÷ 2 = 1051 remainder 1
1051 ÷ 2 = 525 remainder 1
525 ÷ 2 = 262 remainder 1
0314-4646739 0332-4646739 03364646739

262 ÷ 2 = 131 remainder 0
131 ÷ 2 = 65 remainder 1
65 ÷ 2 = 32 remainder 1
32 ÷ 2 = 16 remainder 0
16 ÷ 2 = 8 remainder 0
0314-4646739 0332-4646739 03364646739

Step 5: The remainders from bottom to top form
representation. So, the binary representation of 67321 is:
10000011110001001
the binary
(ii) Convert 143 into binary:
Step 1: Start with the decimal number (143).
Step 2: Divide the number by 2, and write down the quotient and the
remainder.
143 ÷ 2 = 71 remainder 1
0314-4646739 0332-4646739 03364646739

Step 3: Take the quotient from the previous step and repeat the process,
dividing it by 2 and recording the quotient and remainder.
71 ÷ 2 = 35 remainder 1
Step 4: Continue this process until the quotient becomes 0.
35 ÷ 2 = 17 remainder 1
0314-4646739 0332-4646739 03364646739

Step 5: The remainders from bottom to top form the binary
representation. So, the binary representation of 143 is:
10001111
So, the binary representation of 67321 is 10000011110001001, and the binary
representation of 143 is 10001111.
(b) Simplify: {(𝟔𝟖𝟏)𝟏𝟎 ÷ (𝟐𝟐)𝟏𝟎} + (𝟏𝟎𝟏𝟏𝟏𝟎𝟏𝟏)𝟐
0314-4646739 0332-4646739 03364646739

10111011
11111
+
110010010
0314-4646739 0332-4646739 03364646739

0314-4646739 0332-4646739 03364646739

AIOU Solved Assignment Code 1349 Introduction To Business Mathematics Autumn 2023 Assignment 2.pdf

More Related Content

What's hot

Similar to AIOU Solved Assignment Code 1349 Introduction To Business Mathematics Autumn 2023 Assignment 2.pdf

More from Zawarali786

Recently uploaded

AIOU Solved Assignment Code 1349 Introduction To Business Mathematics Autumn 2023 Assignment 2.pdf