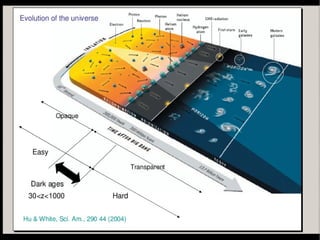
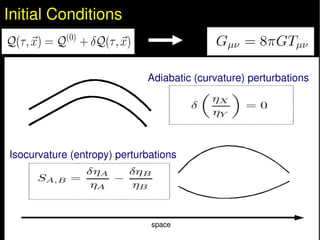
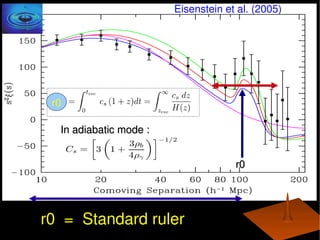
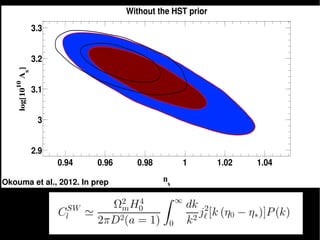
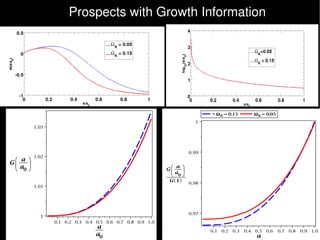
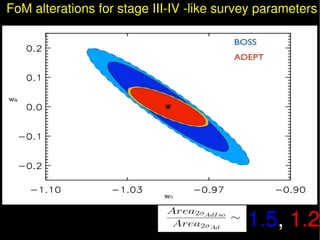
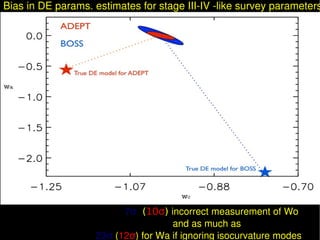
This document summarizes research on the impact of allowing for general isocurvature perturbations and cosmic curvature in analyses of baryon acoustic oscillations (BAO) as a probe of dark energy. The key points are: 1) Accounting for general isocurvature modes could bias dark energy parameter estimates from stage III-IV surveys by over 7 sigma, incorrectly measuring w0 and up to 23 sigma for wa. 2) Including isocurvature modes degrades the dark energy figure of merit from BAO data by at least 50% for experiments like BOSS. 3) BAO provide stronger constraints on the primordial perturbations than CMB alone. Allowing dynamical dark energy and curvature adds little

1. Aspects of Dark Energy
and
Cosmic Curvature
Patrice M. OKOUMA
UCT/AIMS/SAAO

3. A Fundamental Uncertainty in
The BAO Scale from Isocurvature Modes
Physics Letters B. 696 (2011), pp. 433­437
The sensitivity of BAO Dark Energy Constraints to
General Isocurvature Perturbations
arXiv:1111.2572v1
Work(s) With C. Zunckel, S. Muya­Kasanda,
K. Moodley (UKZN, SA) ;
B.A. BASSETT (AIMS/UCT/SAAO, SA)

4. Motivation
our current understanding of Baryon Acoustic Oscillations (BAO)
relies on a set of restrictive assumptions about the initial conditions.
Question : Assuming more general initial conditions,
by how much could this assumption alter/bias
our understanding of DE via the BAO scale ?

5. Initial Conditions space
Adiabatic (curvature) perturbations
Isocurvature (entropy) perturbations
space

6. “ Fingerprints ”
on
Large Scale Structure

7. Eisenstein et al. (2005)
r0
In adiabatic mode :
r0
r0 = Standard ruler

8. Fisher formalism applied to galaxy power spectrum
If likelihood function of band powers of galaxy power spectrum is Gaussian
(Tegmark et al. 1997; Seo & Eisenstein 2003)

9. Fisher formalism applied
to galaxy power spectrum – cont'd
+ Isocurvature parameters
Gaussian Likelihood
Minimum error on parameter =

10. FoM alterations for stage III­IV ­like survey parameters
1.5, 1.2

11. Bias in DE params. estimates for stage III­IV ­like survey parameters
7σ (10σ) incorrect measurement of Wo
and as much as
23σ (12σ) for Wa if ignoring isocurvature modes

12.
BAO are a firm prediction of CDM models
and one key­topic of the science programme for SKA;
Even for isocurvature amplitudes undetectable by PLANCK, the
presence of multiple isocurvature modes could lead to biases in the
DE parameters that exceed 7 sigma on average, if the analysis is
done assuming isocurvature initial conditions;
Accounting for all isocurvature modes corrects for this bias but
degrades the DE figure of merit by at least 50% in the case of the
BOSS experiment;
BAO data also provide much stronger constraints on the nature of
the primordial perturbations than from the CMB alone.

13. In adiabatic mode :
r0
r0 = Standard ruler

14. The curvature­dark energy
(geometric) degeneracy through
the CMB
Work with Y. Fantaye (SISSA, Italy)
& B. A. BASSETT (AIMS/UCT/SAAO, SA)

15. OUTLINE
Curvature, lnflation?
What is the Geometric Degeneracy?
Some results
Summary

16. Motivation
The current model of Inflation predicts that spatial
sections of space­time (the Universe) are flat;

Current datasets are consistent with this paradigm
IF the dark energy is a cosmological constant;

We study the impact of allowing for a general
evolution of the dark energy on the geometry of
the Universe and extract some new constraints on
cosmological parameters.

17. Curvature ?
R
R
X
(radius of) Curvature = 1/R ­­­­­­­­­­­> 0
(radius of) Curvature = 1/R K = 1
K = ­1
Curvature density parameter
K = 0

18. Inflation : a solution to some Big Bang puzzles
Larson et al. (2011)
AIMS 2012 18

20. What is the
curvature­dark energy
(geometric) Degeneracy?

21. D. Larson et al. (2010)
21
l1
AIMS 2012

22. The Basic Geometric Degeneracy :
Okouma et al., 2012. In prep
K =
Ωk and Wde effects can cancel each other
1
Using WMAP7 data only,
­­­­­­>same angular power spectrum for
K = ­1 IF WDE = ­1, Then
IF
different sets of these parameters.
Larson et al., 2011
K = 0

23. The general geometric degeneracy

24. The curvature­dark energy
(geometric) degeneracy through the
CMB

25. Bayes Theorem:
Metropolis­Hastings algorithm for the sampling of the posterior pdf
­­­> Random walk in parameter space using a modified CosmoMC
Data: WMAP7­yr , Supernovae, BBN, HST (+ ACT data)
B. Bassett stat. lectures
5 chains of 300 000 steps each ran

26. Some Results
Okouma et al., 2012. In prep

27. Oohh Look !
Okouma et al., 2012. In prep
Okouma et al., 2011. In prep
using CAMB
H0 = 71 (km/s)/Mpc,
Ok = 0.15
H0 = 56.36 (km/s)/Mpc,
Ok = ­0.06 AIMS 2012 27

28. ?
Okouma et al., 2012. In prep

29. Okouma et al., 2012. In prep

30. Large open models with dynamical DE which fit the
first CMB peak do exist, but the strong Integrated
Sachs­Wolfe (ISW) effect in such models means
that low multipoles of the CMB power spectrum is
very poorly fit, hence these models are discarded.
The vast ~ 30­dimensional parameter volume
explored is an additional limitation.

31. X
√

32. 
A significantly non­phantom (Wde > ­1) leads to a
strong reduction in the volume of possible curved
models;

A general dynamical dark energy model adds nothing
significant in terms of allowing for curved models;

Strong constraints on cosmic curvature remain despite
the extra dark energy freedom. However, these
constraints now come from a mixture of dynamical
constraints (ISW effect) and distance measurements.

34. Okouma et al., 2012. In prep

35. Okouma et al., 2012. In prep
J­Q Xia & M. Viel , 2009

36. Okouma et al., 2012. In prep

37. Okouma et al., 2012. In prep
Komatsu et al., 2008

38. Okouma et al., 2012. In prep

40. Prospects with Growth Information

41. Summary
A general dynamical dark energy model adds nothing
significant in terms of allowing for curved models;
Strong constraints on cosmic curvature remain despite
the extra dark energy freedom.
However, these constraints now come from a mixture of
dynamical constraints (Integrated Sachs­Wolfe effect) and
distance measurements.

42. Thank you
for
your attention