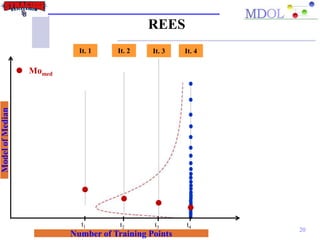
This document presents a new 3-level approach to simultaneously select the best surrogate model type, kernel function, and hyper-parameters for approximation models. The approach uses Regional Error Estimation of Surrogates (REES) to evaluate error and select models. It compares a cascaded technique that performs sequential optimization versus a one-step technique. Numerical examples on benchmark problems show the one-step technique reduces maximum and median errors by at least 60% with lower computational cost compared to the cascaded approach. Future work involves applying the one-step method to more complex problems and developing an online platform for collaborative surrogate model selection.

1. A Novel Approach to Simultaneous Selection of
Surrogate Models, Constitutive Kernels, and
Hyper-parameter Values
Ali Mehmani*, Souma Chowdhury#, and Achille Messac#
* Syracuse University, Department of Mechanical and Aerospace Engineering
# Mississippi State University, Bagley College of Engineering
10th Multi-Disciplinary Design Optimization Conference
AIAA Science and Technology Forum and Exposition
January 13 – 17, 2014 National Harbor, Maryland

2. Surrogate model
• Surrogate models are commonly used for providing a tractable and
inexpensive approximation of the actual system behavior in many
routine engineering analysis and design activities:
2

3. Surrogate model
• Surrogate models are commonly used for providing a tractable and
inexpensive approximation of the actual system behavior in many
routine engineering analysis and design activities:
3
Kriging . . .Model Type RBF SVR
Kernel / basis function
Linear Exponential Gaussian Cubic Multiquadric . . .
Hyper-parameter
Correlation parameter Shape parameter . . .
𝒇 𝒙 =
𝒊=𝟏
𝒏
𝒘𝒊 𝝍( 𝒙 − 𝒙𝒊
)
𝝍 𝒓 = (𝒓 𝟐
+ 𝒄 𝟐
) 𝟏/𝟐
𝒓= 𝒙 − 𝒙𝒊
𝒄𝒍𝒐𝒘𝒆𝒓
< 𝒄 < 𝒄 𝒖𝒑𝒑𝒆𝒓

4. Research Objective
 Develop a new model selection approach, which
simultaneously select the best model type, kernel function, and
hyper-parameter.
4
Types of model Types of basis/kernel Hyper-parameter(s)
• RBF,
• Kriging,
• E-RBF,
• SVR,
• QRS,
• …
• Linear
• Gaussian
• Multiquadric
• Inverse multiquadric
• Kriging
• …
• Shape parameter in RBF,
• Smoothness and width
parameters in Kriging,
• Kernel parameter in SVM,
• …

5. Presentation Outline
5
• Surrogate model selection
• REES-based Model Selection
• 3-Level model selection
• Regional Error Estimation of Surrogate (REES)
• Numerical Examples
• Concluding Remarks

6. Surrogate model selection
6
• Dimension and nature of sample points,
• Level of a noise,
• Application domain,
• …
Suitable Surrogate
Error measures are used to
select the best surrogate
Experienced-based model selection
Automated model selection
• RMSE,
• Cross-validation,
• REES,
• …
 Hyper-parameter selection (Kriging-Guassian) using cross validation and
maximum likelihood estimation (Martin and Simpson)
 Model type and basis function selection using cross validation (Viana and Haftka)
 Model type selection using leave-one-out cross validation (Drik Gorisson et al.)

7. 3-Level model selection
7
 In 3-level model selection, the selection criteria could depend
on the user preference.
Standard surrogate-based analysis
Structural optimization applications
lower median error
lower maximum error

8. 3-Level model selection
8
Median error
Maximum error
Two model selection criteria
evaluated using advanced surrogate error
estimation method presented in REES
 Depending on the problem and the available data set, the
median and maximum errors might be
mutually conflicting
mutually promoting
Pareto models
A single optimum model

9. 3-Level model selection
9
 To implement a 3-level model selection, two approaches are
proposed:
(i) Cascaded technique, and
(ii) One-Step technique.

10. 3-Level model selection
10
Cascaded technique
 For each candidate kernel function, hyper-parameter optimization is
performed to minimize the median and maximum error.
 Post hyper-parameter optimizations,
Pareto filter is used to reach the final
Pareto models.
 Hyper-parameter optimization is
the process of quantitative search to
find optimum hyper-parameter
value(s).

11. 3-Level model selection
11
Cascaded technique
Solutions of the hyper-parameter optimization in the cascaded
technique for multiquadric basis function of RBF surrogate for
Baranin-hoo function

12. 3-Level model selection
12
One-Step technique
 To escape the potentially high computational cost of the cascaded
technique
Subjected to
The three-level model selection could also be performed by solving
a single uniquely formulated mixed integer nonlinear
programming (MINLP) problem.
model type
basis function
hyper-parameter(s)

13. Regional Error Estimation of Surrogate
(REES)
13
The REES method is derived from the hypothesis that the accuracy of
approximation models is related to the amount of data resources
leveraged to train the model.
• Mehmani, A., Chowdhury, S., Zhang, Jie, and Messac, A., “Quantifying Regional Error in
Surrogates by Modeling its Relationship with Sample Density,” 54th
AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference,
Paper No. AIAA 2013-1751, Boston, Massachusetts, April 8-11, 2013.
• Mehmani, et. al., “Model Selection based on Generalized-Regional Error Estimation for
Surrogate,” 10th World Congress on Structural and Multidisciplinary Optimization, Paper No.
5447, Orlando, Florida, May 19-24, 2013.
• Mehmani, et. al.., “Regional Error Estimation of Surrogates (REES),” 14th AIAA/ISSMO
Multidisciplinary Analysis and Optimization Conference, Paper No. AIAA 2012-5707,
Indianapolis, Indiana, September 17-19, 2012.

14. REES
Sample Point
Surrogate Model
Training Point

15. Test Point
Training Point
1st Iter.
2nd Iter.
3rd Iter.
4th Iter.
Error
Surrogate
ε1
ε2
ε3
ε4
?
8 16
12 12
16 8
20 4
24 0
1st
2nd
3rd
4th
REES

16. Test Point
Training Point
1st
MedianofRAEs
1st
ε = 𝒎𝒆𝒅 |
𝒇𝒊 − 𝒇𝒊
𝒇𝒊
| ,
𝐢 = 𝟏, … , 𝟏𝟔
Actual modelIntermediate
surrogate model
...
REES
16

17. 17
MedianofRAEs
Momed
Number of Training Points
t1 t2 t3 t4
It. 1
REES

18. 18
MedianofRAEs
Number of Training Points
t1 t2 t3 t4
Momed
It. 2It. 1
REES

19. 19
MedianofRAEs
Number of Training Points
t1 t2 t3 t4
Momed
It. 3It. 2It. 1
REES

20. 20
It. 3It. 1
MedianofRAEs
Number of Training Points
t1 t2 t3 t4
It. 2
Momed
It. 4
ModelofMedian
REES

21. 21
It. 3It. 1
MedianofRAEs
Number of Training Points
t1 t2 t3 t4
It. 2
Momed
It. 4
ModelofMedian
Predicted Median Error
REES

22. 22
It. 3It. 1
MedianofRAEs
Number of Training Points
t1 t2 t3 t4
It. 2
Momed
It. 4
ModelofMedian
Momax Mode of maximum
error distribution at
each iteration
Predicted Median Error
Predicted Maximum Error
REES

23. 23
The effectiveness of the new 3-level model selection method is
investigated by considering the following three candidate surrogates:
The methods are implemented on three benchmark problems and an
engineering design problem are tested.
Gaussian basis function
Multiquadric basis function
Gaussian correlation function
Exponential correlation function
Radial basis kernel function
Sigmoid kernel function
SVR
RBF
Kriging
Model type Kernel function Hyper-parameter
Numerical Examples

24. 24
Numerical Setting
 The numerical settings for the implementation of REES-based model selection
for the benchmark problems
 The numerical settings for the hyper-parameter optimization
Numerical Examples
24

25. 25
Hyper-parameter optimization of Cascaded technique in different surrogate type and
Kernel functions for Branin-Hoo function with 2 design variables
Numerical Examples

26. 26
Numerical Setting
 The numerical settings for One-Step technique
Integer design variables
Numerical Examples

27. 27
Results; Branin-hoo 2 design variables
Computational cost
One-Step Technique
Cascaded technique
RBF-Multiquadric

28. 28
Cascaded technique
Actual error
RBF-Multiquadric
One-Step Technique
Results; Branin-hoo 2 design variables
RBF-Multiquadric

29. 29
Computational cost
One-Step Technique
Cascaded technique
Results; Hartmann function with 6 design variables
SVR-Radial basis

30. 30
Cascaded technique
Results; Hartmann function with 6 design variables
One-Step Technique
SVR-Radial basis
Actual error
SVR-Radial basis

31. 31
Computational cost
Cascaded technique
Results; Dixon & Price function with 18 design variables
One-Step Technique
RBF-Multiquadric

32. 32
Cascaded technique
One-Step Technique
RBF-Multiquadric
Actual error
RBF-Multiquadric
Results; Dixon & Price function with 18 design variables

33. 33
Numerical Examples
Initial Value Final Solution
Emax EmaxEmax
Emed Emed Emed
RBF-Multiquadric (C=0.9)

34. 34
Concluding Remarks
 A new 3-level model selection approach is developed to select the best
surrogate among available surrogate candidates based on the level of
accuracy.
 This approach is based on the model independent error measure given by the
Regional Error Estimation of Surrogates (REES) method.
 The preliminary results on problems indicate at least 60% reduction in
maximum and median error values.
(i) model type selection,
(ii) kernel function selection, and
(iii) hyper-parameter selection.

35. 35
Future Work
 Implementation of One-Step technique with
 larger pool of surrogates with different number of kernels
 higher dimensional and more computationally intensive problems
 Develop an open online platform called Collaborative Surrogate
Model Selection (COSMOS) to allow users to submit
- training data for identifying an ideal model from existing pool
of surrogate models, and
- their own new surrogate into the pool of surrogate candidates.
If interested in COSMOS please contact me at amehmani@syr.edu

36. Acknowledgement
 I would like to acknowledge my research adviser
Prof. Achille Messac, and my co-adviser Dr.
Souma Chowdhury for their immense help and
support in this research.
 I would also like to thank my friend and colleague
Weiyang Tong for his valuable contributions to this
paper.
 Support from the NSF Awards is also
acknowledged.
36

37. Questions
and
Comments
37
Thank you

38. Quantifying the mode of median and maximum errors
38

39. 39
A chi-square (χ2) goodness-of-fit criterion is used to select the
type of distribution from a list of candidates such as lognormal,
Gamma, Weibull, logistic, log logistic, inverse Gaussian, and
generalized extreme value distribution.