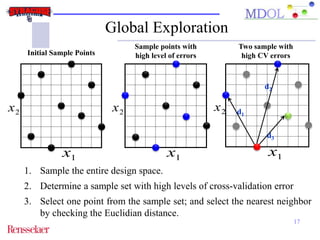
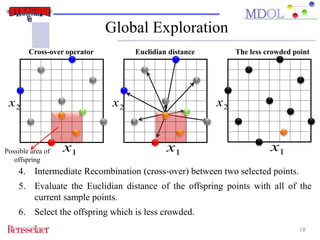
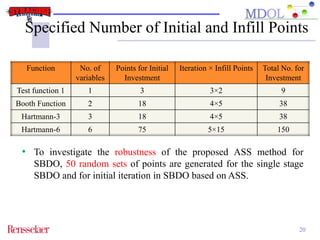
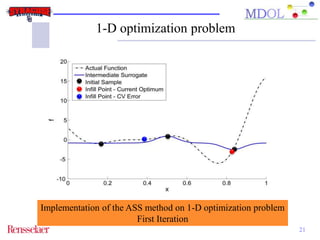
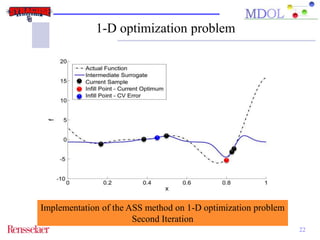
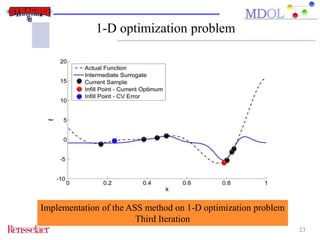
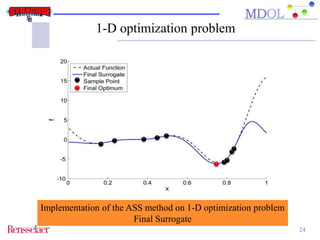
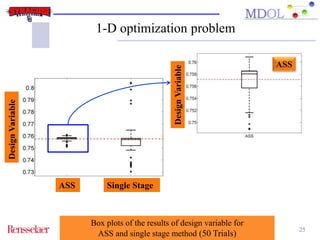
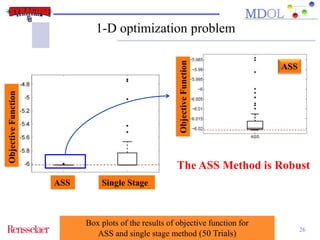
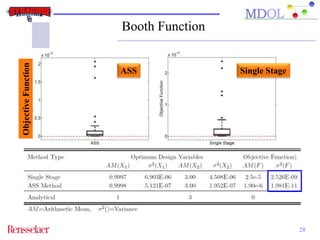
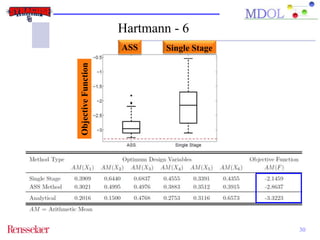
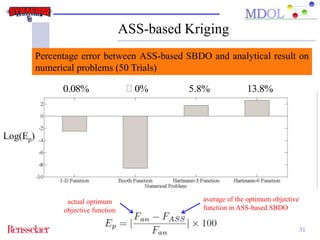
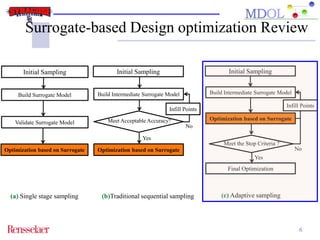
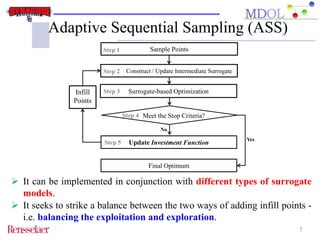
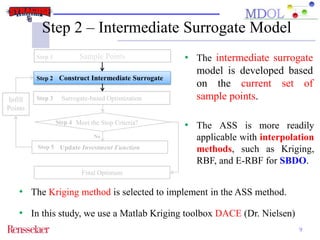
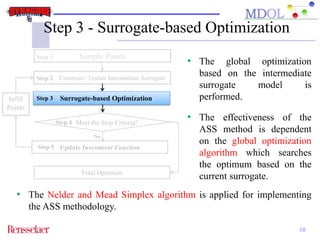
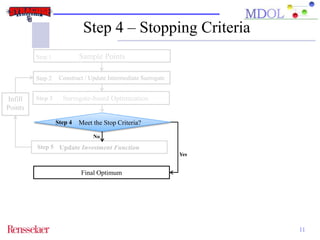
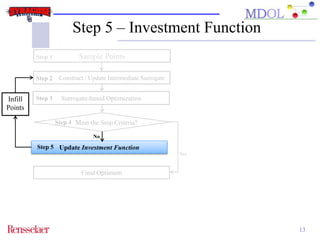
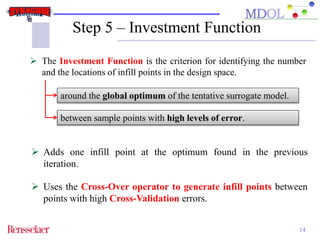
The document discusses the development of an adaptive sequential sampling (ASS) methodology for surrogate-based design optimization (SBDO) aimed at improving the accuracy of surrogate models in engineering design. By strategically adding infill points where surrogates exhibit high error and near the global optimum, the ASS method enhances local exploitation and global exploration, yielding better optimization results. Initial numerical examples validate the effectiveness of the ASS method over traditional single-stage approaches, demonstrating improved efficiency and accuracy.

1. Adaptive Sequential Sampling
for
Surrogate-based Design Optimization
Ali Mehmani*, Jie Zhang#, Souma Chowdhury# and Achille Messac*
* Syracuse University, Department of Mechanical and Aerospace Engineering
# Rensselaer Polytechnic Institute, Department of Mechanical, Aerospace, and Nuclear Engineering
53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and
Materials Conference,
23 - 26 April 2012
Honolulu, Hawaii

2. Surrogate-based Optimization - Overview
• Design optimization problems often involve computationally
intensive simulation models or expensive experiment-based
system evaluations.
• Use of mathematical approximation models (Surrogate) in
design optimization are effective tools for reducing the
computational cost and filtering numerical noise of these
simulation models.
• In surrogate-based design optimization, expensive objective
and/or constraint functions are substituted by accurate surrogate
models.
2

3. Research Motivation
 In spite of the recent developments in surrogate modeling
techniques, the low fidelity of these models often limits their use in
practical engineering design optimization.
 When such surrogates are used for optimization, it becomes
challenging to find the optimum/optima with certainty.
 Sequential sampling methods offer a powerful solution to this
challenge by providing the surrogate with reasonable accuracy
where and when needed.
3

4. Research Objectives
 Develop a new methodology to perform surrogate-based
design optimization using a sequential sampling method to
improve the accuracy of the surrogate in
• the region of the current global optimum (local exploitation) and,
• the regions of higher relative errors (global exploration).
 The proposed method adds infill points in the region of global
optimum as well as in the locations where the surrogate model
has relatively high errors.
4

5. Presentation Outline
• Surrogate-based Design Optimization Review
• Adaptive Sequential Sampling method for SBDO
 Cross-Validation error
 Cross-Over operator
 Surrogate-based design optimization by using ASS method
• Numerical examples: results and discussion
• Concluding remarks
5

6. Surrogate-based Design optimization Review
6
Initial Sampling
Build Surrogate Model
Validate Surrogate Model
Optimization based on Surrogate
Initial Sampling
Build Intermediate Surrogate Model
Infill Points
Meet Acceptable Accuracy?
Yes
Optimization based on Surrogate
No
Initial Sampling
Build Intermediate Surrogate Model
Optimization based on Surrogate
Meet the Stop Criteria ?
(a) Single stage sampling (b)Traditional sequential sampling (c) Adaptive sampling
Infill Points
Final Optimization
No
Yes

7. Adaptive Sequential Sampling (ASS)
 It can be implemented in conjunction with different types of surrogate
7
Sample Points
Construct / Update Intermediate Surrogate
Surrogate-based Optimization
Update Investment Function
Final Optimum
Step 1
Step 2
Step 3
Step 4 Meet the Stop Criteria?
No
Infill
Points
Yes
Step 5
models.
 It seeks to strike a balance between the two ways of adding infill points -
i.e. balancing the exploitation and exploration.

8. Step 1 – Initial Sample Points
Sample Points
Construct / Update Intermediate Surrogate
Surrogate-based Optimization
Update Investment Function
• Latin Hypercube (LH) sampling is applied to sample the whole design
8
space in the first iteration in ASS.
Infill
Points
Final Optimum
Step 1
Step 2
Step 3
Step 4 Meet the Stop Criteria?
No
Step 5
• A set of initial sampling points
are generated at the first
iteration.
• The distribution of the sample
points in design space has a
considerable effect on ASS.

9. Step 2 – Intermediate Surrogate Model
• The intermediate surrogate
model is developed based
on the current set of
sample points.
• The ASS is more readily
applicable with interpolation
methods, such as Kriging,
RBF, and E-RBF for SBDO.
9
Sample Points
Construct Intermediate Surrogate
Surrogate-based Optimization
Step 4 Meet the Stop Criteria?
No
Update Investment Function
Final Optimum
Step 1
Step 2
Step 3
Infill
Points
Step 5
• The Kriging method is selected to implement in the ASS method.
• In this study, we use a Matlab Kriging toolbox DACE (Dr. Nielsen)

10. Step 3 - Surrogate-based Optimization
• The effectiveness of the
ASS method is dependent
on the global optimization
algorithm which searches
the optimum based on the
current surrogate.
Sample Points
Construct / Update Intermediate Surrogate
Surrogate-based Optimization
Step 4 Meet the Stop Criteria?
No
Update Investment Function
Final Optimum
Step 1
Step 2
Step 3
• The Nelder and Mead Simplex algorithm is applied for implementing
10
the ASS methodology.
Infill
Points
Step 5
• The global optimization
based on the intermediate
surrogate model is
performed.

11. Step 4 – Stopping Criteria
11
Sample Points
Construct / Update Intermediate Surrogate
Surrogate-based Optimization
Update Investment Function
Final Optimum
Step 1
Step 2
Step 3
Step 4
Meet the Stop Criteria?
No
Infill
Points
Step 5
Yes

12. Step 4 – Stopping Criteria
Three different methods can be used as the stopping criteria:
(i) The difference between optimum values of two consecutive
12
iterations is smaller than a threshold value,
(ii) The maximum number of sample points allowed (total investment)
is reached, and
(iii)The change in the investment function value is smaller than a
defined threshold value over consecutive iteration.

13. Step 5 – Investment Function
13
Sample Points
Construct / Update Intermediate Surrogate
Surrogate-based Optimization
Update Investment Function
Final Optimum
Step 1
Step 2
Step 3
Step 4 Meet the Stop Criteria?
No
Infill
Points
Step 5
Yes

14. Step 5 – Investment Function
 The Investment Function is the criterion for identifying the number
14
and the locations of infill points in the design space.
around the global optimum of the tentative surrogate model.
between sample points with high levels of error.
 Adds one infill point at the optimum found in the previous
iteration.
 Uses the Cross-Over operator to generate infill points between
points with high Cross-Validation errors.

15. Cross-Validation
• The Relative Accuracy Error (RAE) which is derived from leave-one-
out strategy is applied to measure the Cross-Validation errors
15
at each current sample points.
• A set of sample points with high levels of cross-validation
error are determined.
Actual
function value
Estimated value
by surrogate

16. Cross-Over
• This operator is used to combine information from two current
16
sample points with high levels of cross-validation error.
• The Intermediate Recombination method is only applicable to real
variables to combine the genetic material of two parents.
α represents a scaling factor, and is chosen randomly between the
interval [−d, 1 + d].
• In this study, the standard intermediate recombination is used and
the value of d is assumed to be zero (d = 0)

17. Global Exploration
17
1 x
2 x
1 x
2 x
1. Sample the entire design space.
2. Determine a sample set with high levels of cross-validation error
3. Select one point from the sample set; and select the nearest neighbor
by checking the Euclidian distance.
1 x
2 x d1
d2
d3
Initial Sample Points
Sample points with
high level of errors
Two sample with
high CV errors

18. Global Exploration
Cross-over operator Euclidian distance The less crowded point
18
Possible area of
offspring
1 x
2 x
1 x
2 x
1 x
2 x
4. Intermediate Recombination (cross-over) between two selected points.
5. Evaluate the Euclidian distance of the offspring points with all of the
current sample points.
6. Select the offspring which is less crowded.

19. Numerical Examples
• The ASS method is validated using the following numerical test
19
problems:
1) 1-variable function;
2) Booth function;
3) Hartmann function with 3 variables; and
4) Hartmann function with 6 variables.

20. Specified Number of Initial and Infill Points
20
Function No. of
variables
Points for Initial
Investment
Iteration × Infill Points Total No. for
Investment
Test function 1 1 3 3×2 9
Booth Function 2 18 4×5 38
Hartmann-3 3 18 4×5 38
Hartmann-6 6 75 5×15 150
• To investigate the robustness of the proposed ASS method for
SBDO, 50 random sets of points are generated for the single stage
SBDO and for initial iteration in SBDO based on ASS.

21. 21
1-D optimization problem
Implementation of the ASS method on 1-D optimization problem
First Iteration

22. 22
1-D optimization problem
Implementation of the ASS method on 1-D optimization problem
Second Iteration

23. 23
1-D optimization problem
Implementation of the ASS method on 1-D optimization problem
Third Iteration

24. 24
1-D optimization problem
Implementation of the ASS method on 1-D optimization problem
Final Surrogate

25. 25
1-D optimization problem
ASS Single Stage
Box plots of the results of design variable for
ASS and single stage method (50 Trials)
Design Variable
ASS
Design Variable

26. 26
1-D optimization problem
Box plots of the results of objective function for
ASS and single stage method (50 Trials)
ASS
Objective Function
ASS Single Stage
Objective Function
The ASS Method is Robust

27. 1-D optimization problem
Comparison of the performances of ASS and single stage method on 1-D
27
optimization problem (50 Trials)
• The arithmetic mean of the results, the ASS method is more accurate
when compared to the single stage method.
• The variance results over the 50 trials in the ASS-based Kriging is
significantly less than that in the single stage-based Kriging.

28. 28
Booth Function
ASS Single Stage
Objective Function

29. 29
Hartmann - 3
Objective Function
ASS Single Stage

30. 30
Hartmann - 6
Objective Function
ASS Single Stage

31. 31
ASS-based Kriging
Percentage error between ASS-based SBDO and analytical result on
numerical problems (50 Trials)
0.08% 0% 5.8% 13.8%
actual optimum
objective function
average of the optimum objective
function in ASS-based SBDO
Log(Ep)

32. Conclusion and remarks
• We developed the Adaptive Sequential Sampling (ASS) method to
efficiently and accurately find the optimum in surrogate-based
design optimization.
• The ASS improves the local and the global accuracy of the
surrogate model by adding infill points at the optimum as well as
in the regions with high cross-validation errors.
• This method uses the cross-over operator to generate infill points
• The preliminary results indicate that the ASS method improves
the efficiency and the accuracy of SBDO over the single stage
method.
32
between points with high cross-validation errors.
• The ASS method is not limited to specific kind of surrogate
modeling techniques.

33. Future work
• Apply other robust heuristic algorithms such as Particle
33
Swarm Optimization to perform SBDO
• Apply special criteria for adaptively identifying the suitable
number of infill points at each iteration during the SBDO
process.

34. Acknowledgement
• I would like to acknowledge my research adviser Prof.
Achille Messac, for his immense help and support in this
research.
• I would also like to thank my friends and colleagues Jie
Zhang and Souma Chowdhury for their valuable
contributions to this paper.
• Support from the NSF Awards is also acknowledged.
34

35. Thank you
Questions
and
Comments