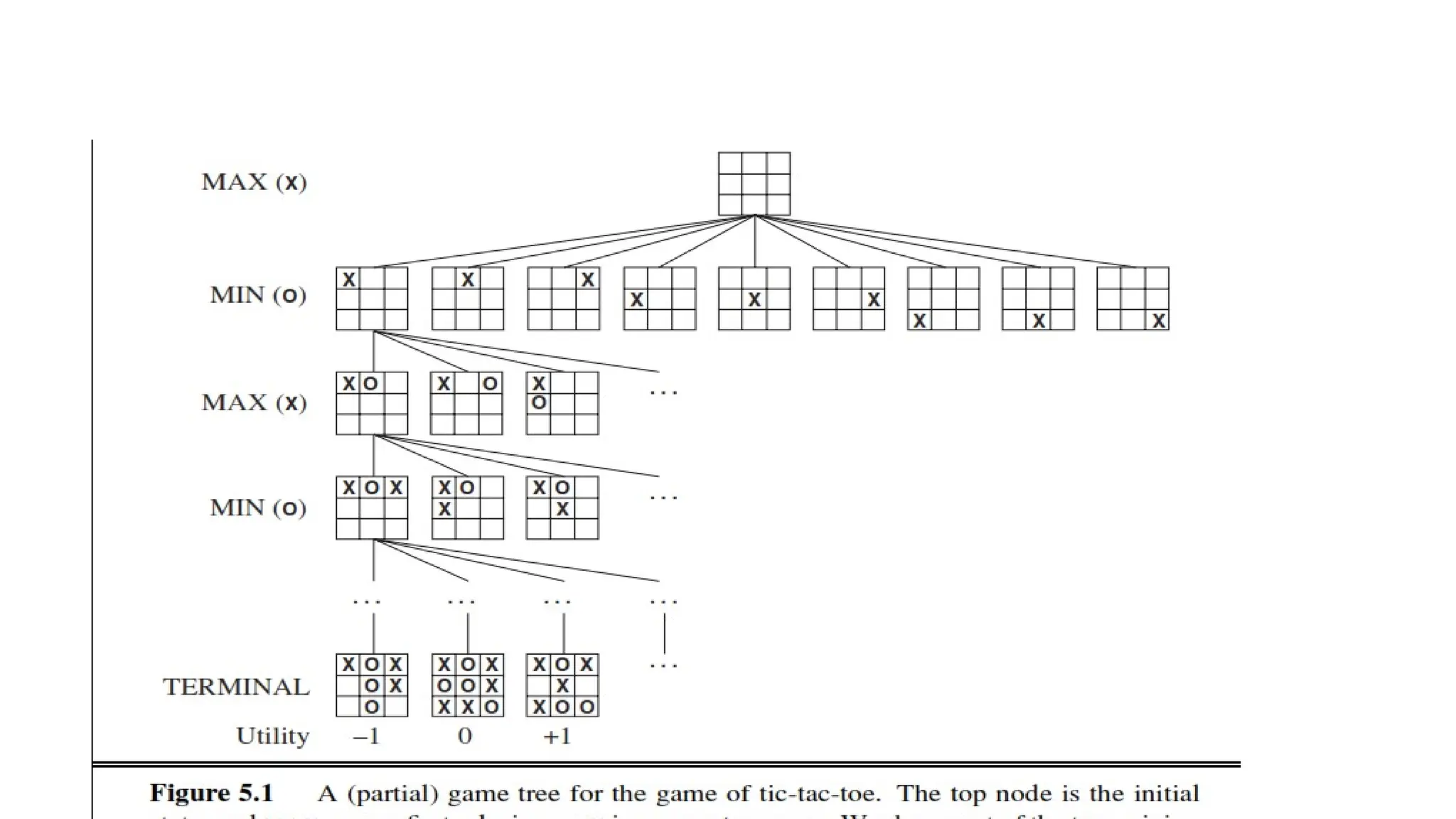
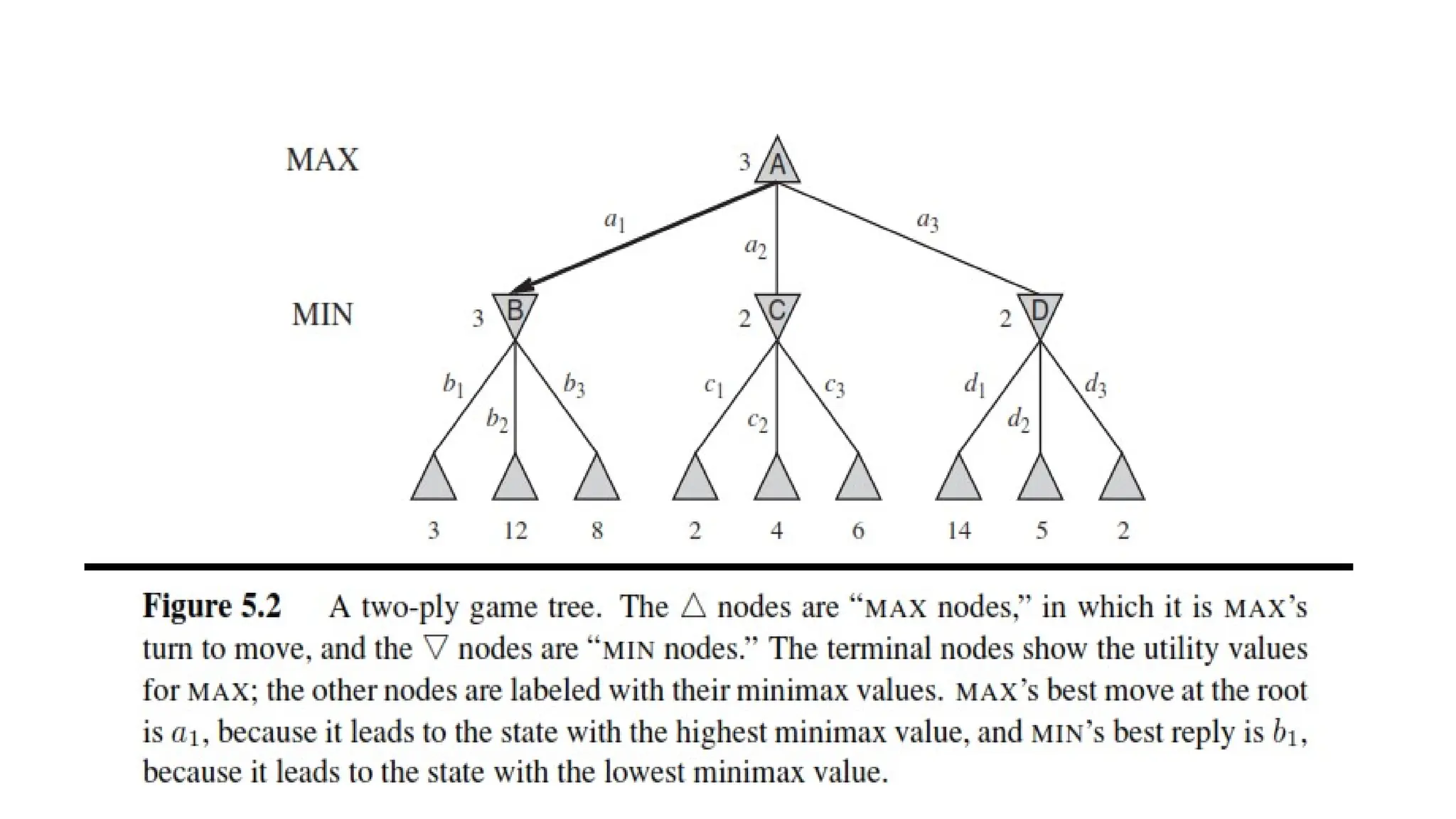
Chapter 2 introduced multiagent environments, in which each agent needs to consider the actions of other agents and how they affect its own welfare. The unpredictability of these other agents can introduce contingencies into the agent’s problem-solving process, as discussed in Chapter 4. In this chapter we cover competitive environments, in which the agents’ goals are in conflict, giving rise to adversarial search problems—often known as games. Mathematical game theory, a branch of economics, views any multiagent environment as a game, provided that the impact of each agent on the others is “significant,” regardless of whether the agents are cooperative or competitive. 1 In AI, the most common games are of a rather specialized kind—what game theorists call deterministic, turn-taking, two-player, zero-sum games of perfect information (such as chess). In our terminology, this means deterministic, fully observable environments in which two agents act alternately and in which the utility values at the end of the game are always equal and opposite. For example, if one player wins a game of chess, the other player necessarily loses. It is this opposition between the agents’ utility functions that makes the situation adversarial. Games have engaged the intellectual faculties of humans—sometimes to an alarming degree—for as long as civilization has existed. For AI researchers, the abstract nature of games makes them an appealing subject for study. The state of a game is easy to represent, and agents are usually restricted to a small number of actions whose outcomes are defined by precise rules. Physical games, such as croquet and ice hockey, have much more complicated descriptions, a much larger range of possible actions, and rather imprecise rules defining the legality of actions. With the exception of robot soccer, these physical games have not attracted much interest in the AI community.

1.  Search Tree: A tree where nodes represent states and edges represent
actions.
o Root Node: Represents the initial state.
o Branches: Represent actions leading to new states.
o Leaf Nodes: Nodes with no children, representing possible end
states.
 Search Graph: Similar to a search tree but avoids redundant paths by
remembering explored states.
Search Trees and Graphs

2. Basic Search Algorithms
 Tree-Search Algorithm:
o Explores all possible paths to find a solution.
o May encounter redundant paths and loops.
 Graph-Search Algorithm:
o Avoids redundant paths by keeping track of explored states.
o More efficient than tree-search in avoiding loops and redundant paths.

3. Key Components of Search Algorithms
 State: A representation of the current situation.
 Action: An operation that transitions from one state to another.
 Transition Model: Describes the result of applying an action to a state.
 Goal Test: Determines if a given state is a goal state.
 Path Cost: The cost associated with a sequence of actions leading to a
state.

4. Search Strategies
 Breadth-First Search (BFS):
o Explores the shallowest nodes first.
o Complete and optimal for unit step costs but has high space
complexity.
 Uniform-Cost Search:
o Expands the node with the lowest path cost.
o Optimal for general step costs but can be slow.

5.  Depth-First Search (DFS):
o Explores the deepest nodes first.
o Not complete or optimal but has low space complexity.
 Depth-Limited Search:
o DFS with a depth limit to avoid infinite paths.
o Can be incomplete if the depth limit is too low.
 Iterative Deepening Search (IDS):
o Combines BFS and DFS by gradually increasing the depth limit.
o Complete and optimal for unit step costs with moderate space complexity.

6.  Bidirectional Search:
o Runs two simultaneous searches from the initial state and the goal
state.
o Can significantly reduce time complexity but requires more space.

7. Measuring Performance
 Completeness: Whether the algorithm guarantees finding a solution if one
exists.
 Optimality: Whether the algorithm guarantees finding the best solution.
 Time Complexity: How long the algorithm takes to find a solution.
 Space Complexity: How much memory the algorithm uses during the
search.

8. Practical Considerations
 Redundant Paths: Multiple ways to reach the same state can increase
complexity.
 Loops: Infinite loops can occur in DFS and must be managed.
• Memory Usage: BFS and uniform-cost search can consume large
amounts of memory

9. Introduction to Games
. Multiagent Environments: These require agents to consider the
actions of others, leading to adversarial search problems.
 Types of Games: Focuses on deterministic, turn-taking, two-player,
zero-sum games of perfect information (e.g., chess).

10. Optimal Decisions in Games
Game Tree: Represents the possible moves in a game.
Minimax Algorithm: Used to find the optimal move by assuming both
players play optimally.
Minimax Value: The utility of a node assuming optimal play from both
players

11. Alpha-Beta Pruning
 Pruning: Technique to ignore parts of the search tree that do not
affect the final decision.
 Alpha-Beta Algorithm: Enhances minimax by pruning branches,
making the search more efficient.

12. Imperfect Real-Time Decisions
 Evaluation Functions: Estimate the utility of a game state when the
search is cut off early.
 Quiescence Search: Extends the search to avoid evaluating non-
quiescent positions.
 Horizon Effect: The problem of delaying inevitable outcomes
beyond the search depth.

13. Stochastic Games
 Games with Chance: Include elements of randomness (e.g., dice
rolls in backgammon).
 Expectiminimax Algorithm: Extends minimax to handle chance
nodes by calculating expected values.

14. Alpha-Beta Pruning
Alpha-Beta Pruning is an optimization technique for the Minimax algorithm. It
reduces the number of nodes evaluated in the game tree by eliminating branches
that cannot influence the final decision.
1. Alpha: The best value that the maximizer (MAX) can guarantee at any point.
2. Beta: The best value that the minimizer (MIN) can guarantee at any point.

15. Example: Tic-Tac-Toe
• Let's consider game tree for tic-tac-toe where MAX (X) and MIN (O) have already made a few moves:
• Initial State:
• X | O | X
• ---|---|---
• O | X |
• ---|---|---
• | |

16. MAX's Turn (X)
Step-by-Step Process
1. Generate the Game Tree:
o MAX can place an 'X' in any of the remaining empty squares.
2. Possible Moves:
o Move 1: Place 'X' in the bottom-left corner.
o Move 2: Place 'X' in the bottom-center.
o Move 3: Place 'X' in the bottom-right corner.

17. 1. Evaluate Terminal States:
o For each move, generate the subsequent moves by MIN and evaluate the
terminal states.
2. Assign Utilities:
o Let's assume the following utilities
Move 1: Leads to a draw (utility = 0).
Move 2: Leads to a win for MAX (utility = +1).
Move 3: Leads to a win for MIN (utility = -1).

18. Alpha-Beta Pruning:
o Start with alpha = -∞ and beta = +∞.
o Evaluate Move 1: Utility = 0. Update alpha to 0.
o Evaluate Move 2: Utility = +1. Update alpha to +1.
o Evaluate Move 3: Utility = -1. Since -1 < alpha, prune this branch.

19. • Game Tree with Alpha-Beta Pruning:
Initial State
/ |
Move 1 Move 2 Move 3
(0) (+1) (-1) [Pruned]
MAX's Optimal Move: Move 2 (utility = +1)

20. What is an adversarial search problem?
An adversarial search problem arises in
competitive environments where agents' goals
conflict, such as in games where each agent must
consider the actions of others to optimize their
own outcome.

21. What is the minimax algorithm used for?
• The minimax algorithm is used to find the
optimal move in a game by assuming that both
players play optimally. It calculates the minimax
value of each node in the game tree to
determine the best move.

22. How does alpha-beta pruning improve the efficiency of the
minimax algorithm?
Alpha-beta pruning improves efficiency by eliminating
branches in the game tree that cannot affect the final
decision, thus reducing the number of nodes that need to
be evaluated.

23. What is the purpose of an evaluation function in game-playing
algorithms?
• An evaluation function estimates the utility of a game state
when the search is cut off early. It helps the algorithm make
decisions without having to search all the way to terminal
states.

24. What is the horizon effect, and how does it impact game-
playing algorithms?
• The horizon effect occurs when a game-playing algorithm
delays inevitable outcomes beyond its search depth, leading
to incorrect evaluations. It impacts the algorithm by making it
think a bad situation can be avoided when it cannot.

25. A game can be formally defined as a kind of search problem with the
following elements:
• S0:The initial state, which specifies how the game is set up at the
start.
• PLAYER(s): Defines which player has the move in a state.
• ACTIONS(s): Returns the set of legal moves in a state.
• RESULT(s, a): The transition model, which defines the result of a move
• TERMINAL-TEST(s):Aterminal test, which is true when the game is over
and false States where the game has ended are called terminal states.
• UTILITY(s, p): The utility function (also called an objective function or
payoff function),defines the final numeric value for a game that ends in
terminal state s for a player p.
• The initial state, ACTIONS function, and RESULT function define the
game tree for the game—a tree where the nodes are game states and the
edges are moves.

28. The minimax algorithm
1.Initialization: Start at the root node of the game tree, which represents the current state of the
game.
2.Recursive Exploration: Recursively explore each possible move from the current state. This involves:
1. Generating all possible successor states (children nodes) from the current state.
2. For each successor state, recursively apply the minimax algorithm to compute its minimax value.
3.Leaf Nodes Evaluation: When a leaf node (a terminal state with no further moves) is reached:
1. Apply the utility function to determine the value of the leaf node. This value represents the outcome of the
game from that state (e.g., win, lose, draw).
4.Backing Up Values: As the recursion unwinds, back up the minimax values from the leaf nodes to
the root:
1. For a minimizing player (usually the opponent), select the minimum value among the child nodes.
2. For a maximizing player (usually the current player), select the maximum value among the child nodes.
5.Root Node Decision: Once the values are backed up to the root node, the algorithm selects the
move that leads to the child node with the optimal minimax value (maximum for the maximizing
player).

29. Example
• Suppose the root node has three child nodes with values 3, 12,
and 8.
• The algorithm backs up the minimum value (3) for the
minimizing player.
• Similarly, for other branches, it backs up values like 2 and 2.
• Finally, at the root, it takes the maximum of these values (3, 2,
and 2), resulting in a backed-up value of 3 for the root node.

30. Optimal decisions in multiplayer games
MINIMAX-DECISION Function
• function MINIMAX-DECISION(state)
returns an action
• This function initiates the minimax decision process
from the given state.
• return arg max a ACTIONS(state)
∈
MIN-VALUE(RESULT(state, a))
• It returns the action that maximizes the minimum
value of the resulting state. Essentially, it looks at all
possible actions from the current state, applies the
MIN-VALUE function to the resulting states, and
chooses the action that gives the highest value

31. MAX-VALUE Function
• function MAX-VALUE(state) returns a utility value
 This function computes the maximum utility value for the maximizing
player from the given state.
• if TERMINAL-TEST(state) then return UTILITY(state)
 If the state is a terminal state (end of the game), it returns the utility
value of that state.
• v ← -∞
 Initializes the value v to negative infinity. This is because we are looking
for the maximum value, and any value will be greater than negative
infinity.
• for each a in ACTIONS(state) do
 Iterates over all possible actions from the current state.
• v ← MAX(v, MIN-VALUE(RESULT(state,
a)))
 For each action, it computes the minimum value of the resulting state
(using the MIN-VALUE function) and updates v to be the maximum of v
and this value.
• return v
 Returns the maximum value found.

32. MIN-VALUE Function MIN-VALUE Function
function MIN-VALUE(state) returns a utility value
 This function computes the minimum utility value for the minimizing player from
the given state.
if TERMINAL-TEST(state) then return UTILITY(state)
 If the state is a terminal state, it returns the utility value of that state.
v ← ∞
 Initializes the value v to positive infinity. This is because we are looking for the
minimum value, and any value will be less than positive infinity.
for each a in ACTIONS(state) do
 Iterates over all possible actions from the current state.
v ← MIN(v, MAX-VALUE(RESULT(state, a)))
 For each action, it computes the maximum value of the resulting state (using the
MAX-VALUE function) and updates v to be the minimum of v and this value.
return v
 Returns the minimum value found.