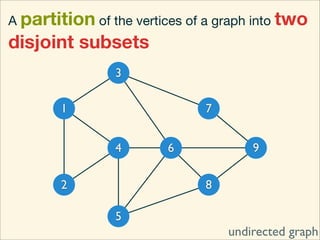
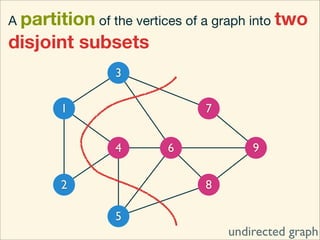
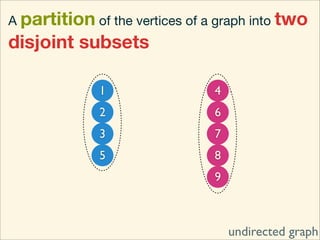
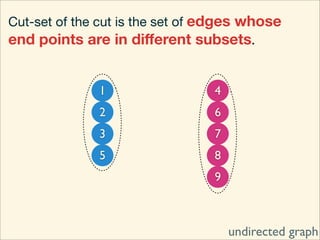
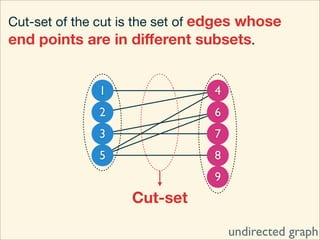
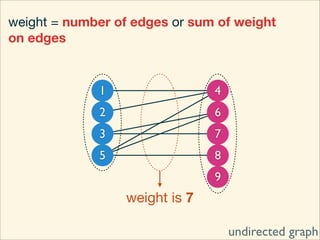
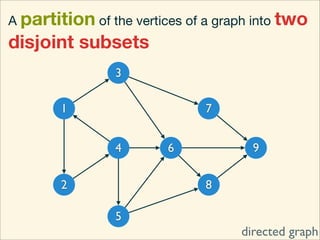
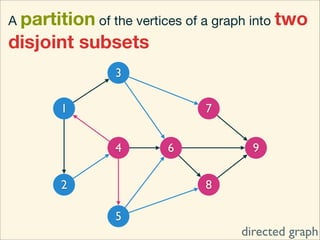
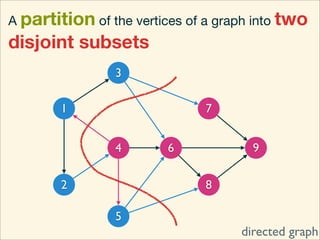
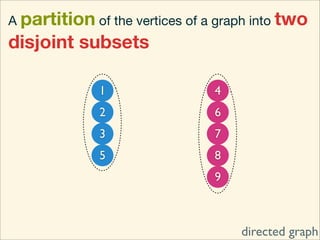
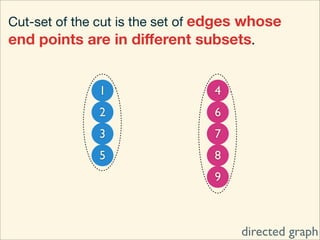
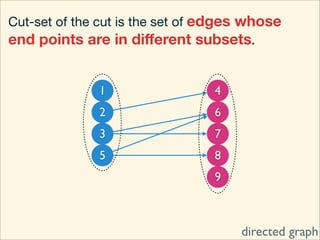
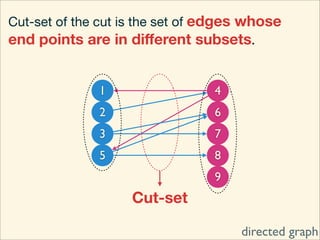
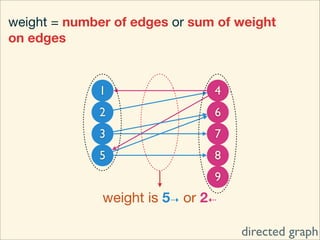
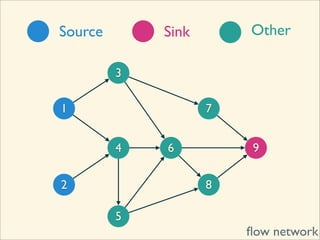
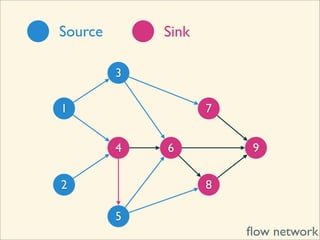
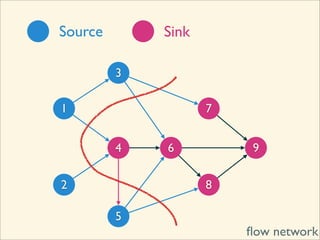
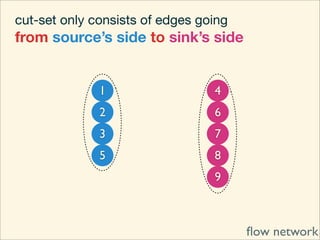
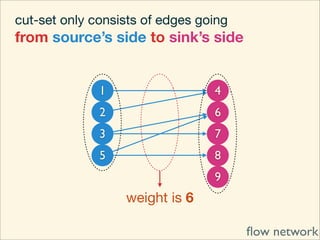
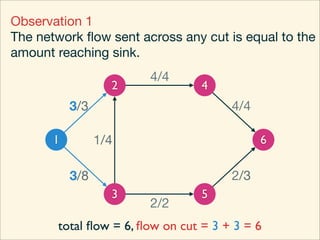
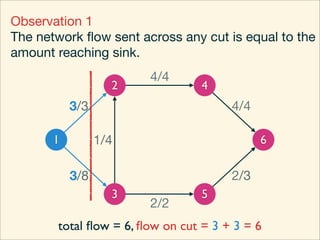
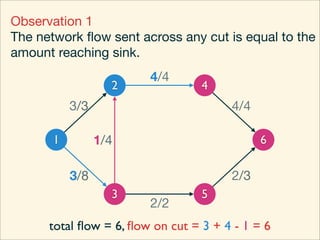
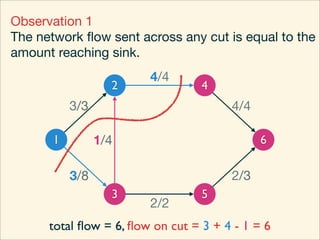
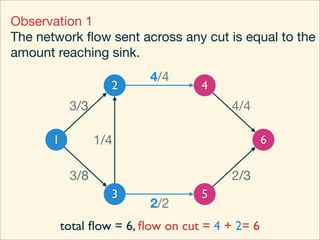
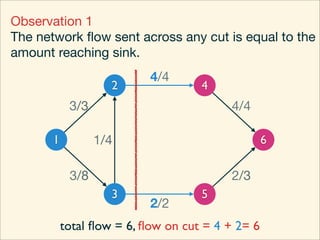
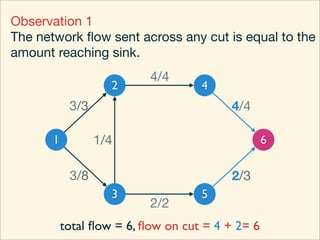
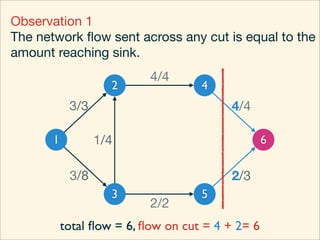
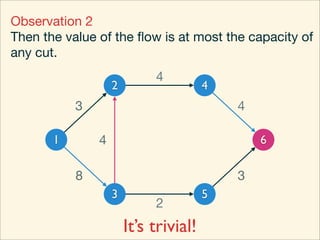
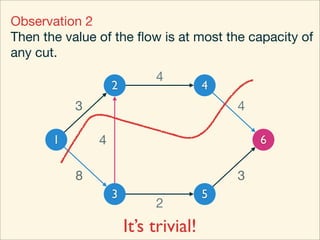
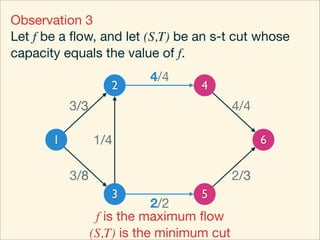
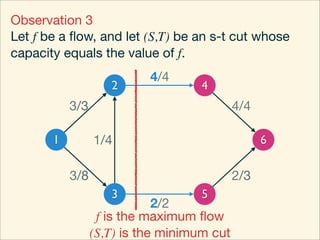
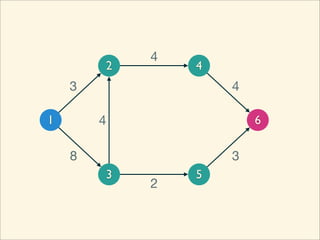
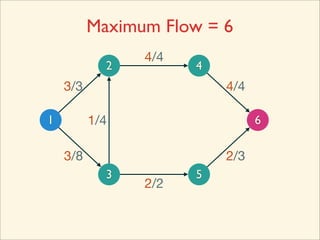
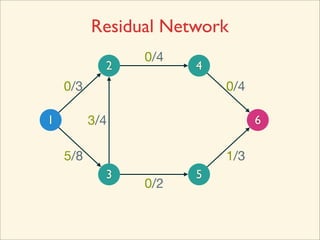
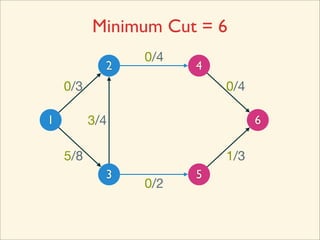
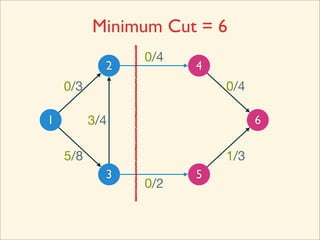
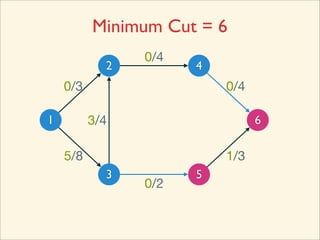
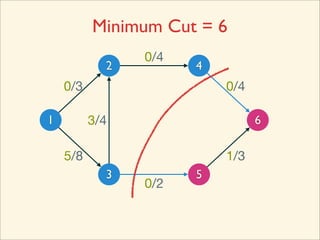
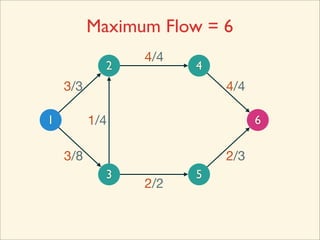
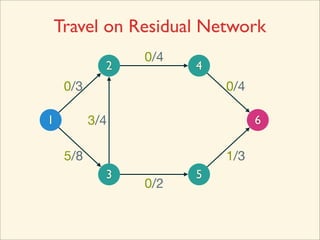
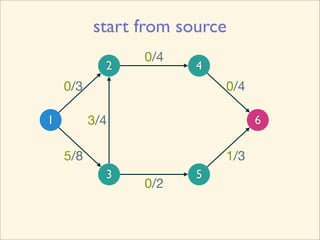
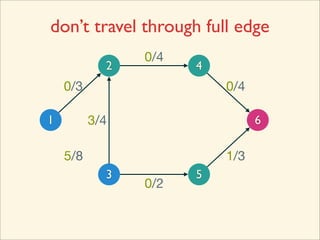
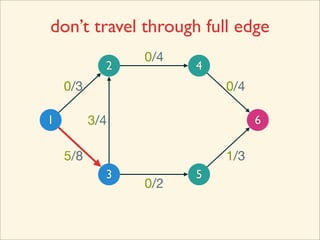
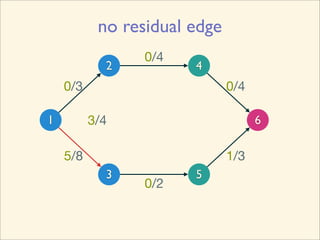
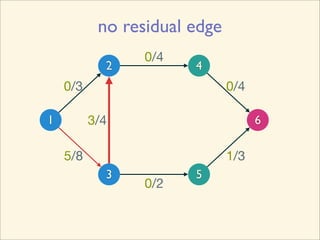
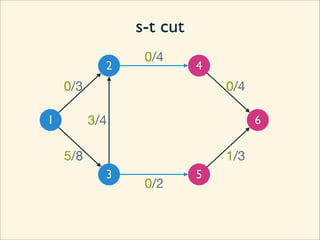
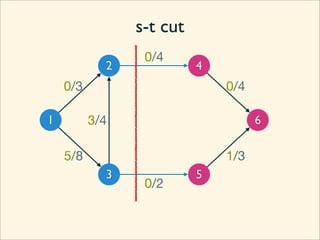
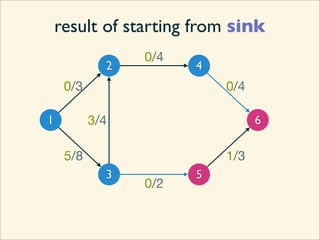
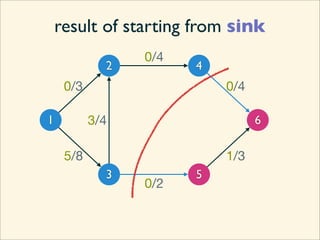
The document discusses minimum cuts in graphs. It defines a minimum cut as a partition of the vertices of a graph into two disjoint subsets such that the number/weight of edges between the two subsets is minimized. For directed graphs, the cut-set of a cut consists only of edges going from one subset to the other. The maximum flow minimum cut theorem states that the maximum amount of flow passing from a source to sink node is equal to the capacity of the minimum s-t cut.

1. Minimum Cut
郭至軒（KuoE0）
KuoE0.tw@gmail.com
KuoE0.ch

2. Cut

3. cut (undirected)

4. A partition of the vertices of a graph into two
disjoint subsets
3
1 7
4 6 9
2 8
5
undirected graph

5. A partition of the vertices of a graph into two
disjoint subsets
3
1 7
4 6 9
2 8
5
undirected graph

6. A partition of the vertices of a graph into two
disjoint subsets
3
1 7
4 6 9
2 8
5
undirected graph

7. A partition of the vertices of a graph into two
disjoint subsets
1 4
2 6
3 7
5 8
9
undirected graph

8. Cut-set of the cut is the set of edges whose
end points are in different subsets.
1 4
2 6
3 7
5 8
9
undirected graph

9. Cut-set of the cut is the set of edges whose
end points are in different subsets.
1 4
2 6
3 7
5 8
9
Cut-set
undirected graph

10. weight = number of edges or sum of weight
on edges
1 4
2 6
3 7
5 8
9
weight is 7
undirected graph

11. cut (directed)

12. A partition of the vertices of a graph into two
disjoint subsets
3
1 7
4 6 9
2 8
5
directed graph

13. A partition of the vertices of a graph into two
disjoint subsets
3
1 7
4 6 9
2 8
5
directed graph

14. A partition of the vertices of a graph into two
disjoint subsets
3
1 7
4 6 9
2 8
5
directed graph

15. A partition of the vertices of a graph into two
disjoint subsets
1 4
2 6
3 7
5 8
9
directed graph

16. Cut-set of the cut is the set of edges whose
end points are in different subsets.
1 4
2 6
3 7
5 8
9
directed graph

17. Cut-set of the cut is the set of edges whose
end points are in different subsets.
1 4
2 6
3 7
5 8
9
directed graph

18. Cut-set of the cut is the set of edges whose
end points are in different subsets.
1 4
2 6
3 7
5 8
9
Cut-set
directed graph

19. weight = number of edges or sum of weight
on edges
1 4
2 6
3 7
5 8
9
weight is 5⇢ or 2⇠
directed graph

20. s-t cut
1. one side is source
2. another side is sink
3. cut-set only consists of edges going
from source’s side to sink’s side

21. Source Sink Other
3
1 7
4 6 9
2 8
5
flow network

22. Source Sink
3
1 7
4 6 9
2 8
5
flow network

23. Source Sink
3
1 7
4 6 9
2 8
5
flow network

24. cut-set only consists of edges going
from source’s side to sink’s side
1 4
2 6
3 7
5 8
9
flow network

25. cut-set only consists of edges going
from source’s side to sink’s side
1 4
2 6
3 7
5 8
9
weight is 6
flow network

26. Max-Flow Min-Cut Theorem

27. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 3 + 3 = 6

28. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 3 + 3 = 6

29. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 3 + 4 - 1 = 6

30. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 3 + 4 - 1 = 6

31. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 4 + 2= 6

32. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 4 + 2= 6

33. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 4 + 2= 6

34. Observation 1
The network flow sent across any cut is equal to the
amount reaching sink.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
total flow = 6, flow on cut = 4 + 2= 6

35. Observation 2
Then the value of the flow is at most the capacity of
any cut.
4
2 4
3 4
1 4 6
8 3
3 5
2
It’s trivial!

36. Observation 2
Then the value of the flow is at most the capacity of
any cut.
4
2 4
3 4
1 4 6
8 3
3 5
2
It’s trivial!

37. Observation 3
Let f be a flow, and let (S,T) be an s-t cut whose
capacity equals the value of f.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
f is the maximum flow
(S,T) is the minimum cut

38. Observation 3
Let f be a flow, and let (S,T) be an s-t cut whose
capacity equals the value of f.
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2
f is the maximum flow
(S,T) is the minimum cut

39. Max-Flow
EQUAL
Min-Cut

40. Example

41. 4
2 4
3 4
1 4 6
8 3
3 5
2

42. Maximum Flow = 6
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2

43. Residual Network
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

44. Minimum Cut = 6
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

45. Minimum Cut = 6
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

46. Minimum Cut = 6
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

47. Minimum Cut = 6
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

48. The minimum capacity
limit
the maximum flow!

49. find a s-t cut

50. Maximum Flow = 6
4/4
2 4
3/3 4/4
1 1/4 6
3/8 2/3
3 5
2/2

51. Travel on Residual Network
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

52. start from source
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

53. don’t travel through full edge
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

54. don’t travel through full edge
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

55. no residual edge
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

56. no residual edge
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

57. s-t cut
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

58. s-t cut
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

59. result of starting from sink
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

60. result of starting from sink
0/4
2 4
0/3 0/4
1 3/4 6
5/8 1/3
3 5
0/2

61. Minimum cut is non-unique!

62. time complexity:
based on max-flow algorithm
Ford-Fulkerson algorithm O(EF)
Edmonds-Karp algorithm O(VE2)
Dinic algorithm O(V2E)

63. Stoer Wagner
only for undirected graph
time complexity: O(N3) or O(N2log2N)

64. Practice Now
UVa 10480 - Sabotage

65. Problem List
UVa 10480
UVa 10989
POJ 1815
POJ 2914
POJ 3084
POJ 3308
POJ 3469

66. Reference
• http://www.flickr.com/photos/dgjones/335788038/
• http://www.flickr.com/photos/njsouthall/3181945005/
• http://www.csie.ntnu.edu.tw/~u91029/Cut.html
• http://en.wikipedia.org/wiki/Cut_(graph_theory)
• http://en.wikipedia.org/wiki/Max-flow_min-cut_theorem
• http://www.cs.princeton.edu/courses/archive/spr04/cos226/lectures/
maxflow.4up.pdf
• http://www.cnblogs.com/scau20110726/archive/
2012/11/27/2791523.html

67. Thank You for Your
Listening.