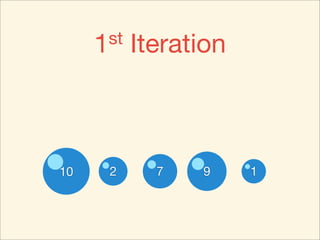
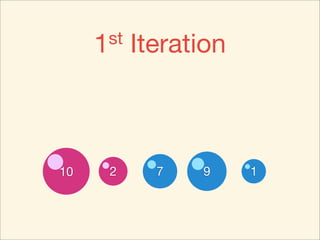
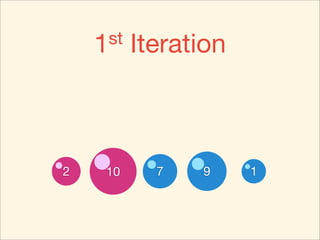
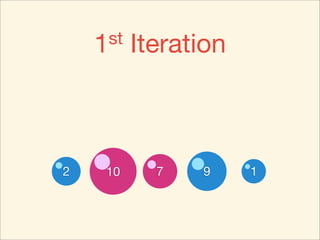
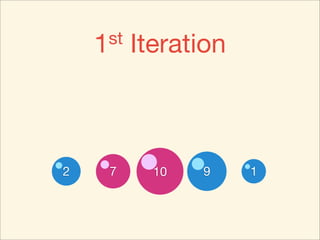
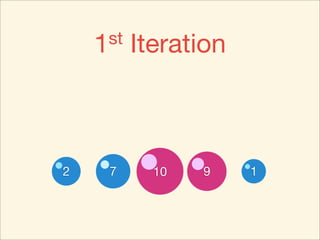
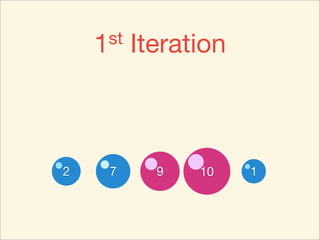
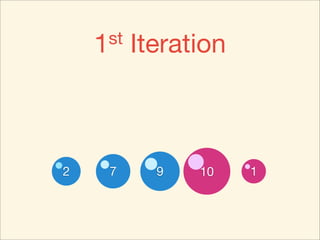
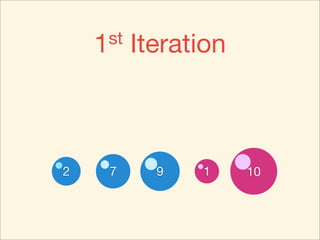
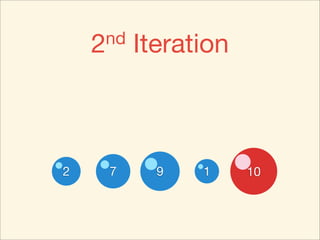
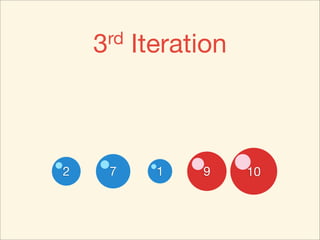
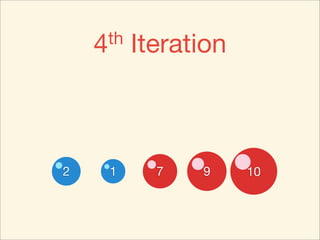
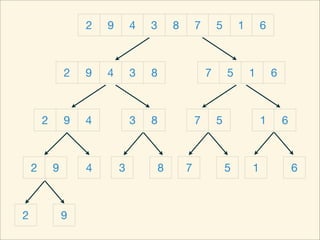
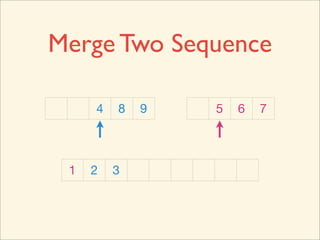
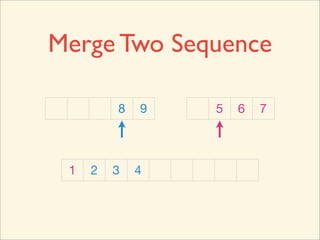
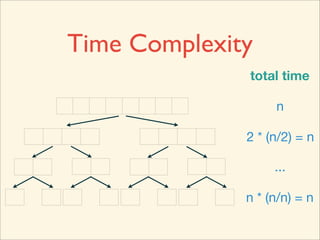
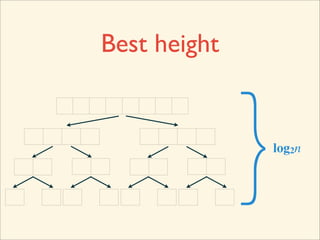
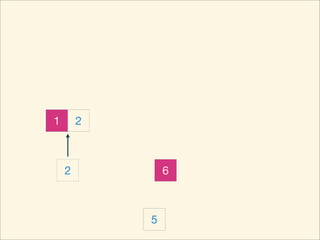
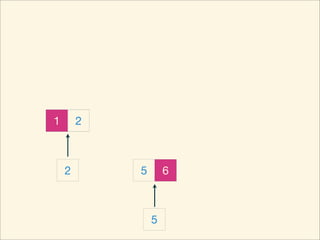
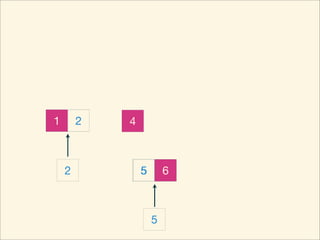
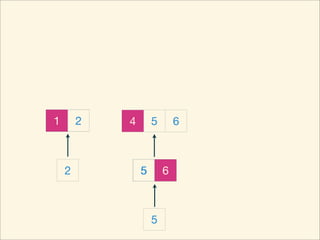
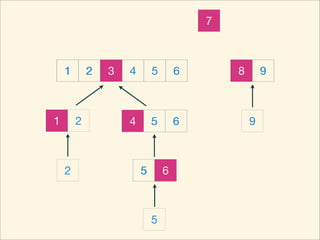
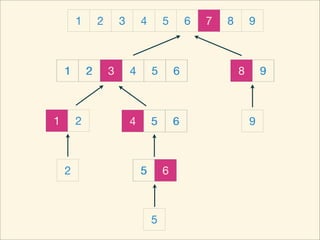
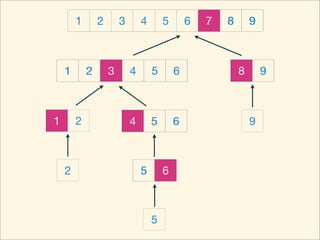
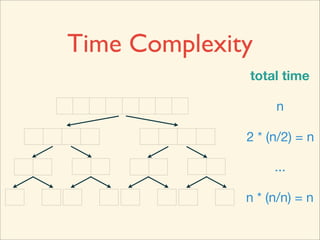
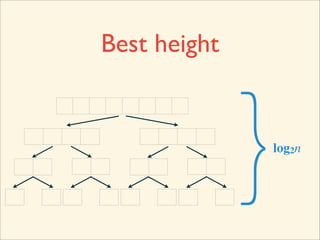
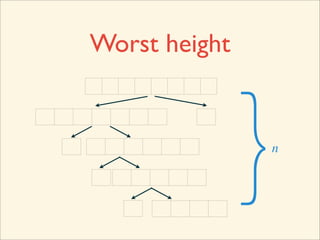
The document describes the bubble sort, merge sort, and quick sort algorithms. Bubble sort has a time complexity of O(n^2) as it may require up to n^2 comparisons in the worst case. Merge sort has a time complexity of O(nlogn) as it divides the list into halves recursively until single elements remain, then merges the sorted halves. Quick sort also has O(nlogn) time as it partitions the list around a pivot element, recursively sorts sublists, and merges the results.

1. Sort
郭至軒（KuoE0）
KuoE0.tw@gmail.com
KuoE0.ch

2. Attribution-ShareAlike 3.0 Unported
(CC BY-SA 3.0)
http://creativecommons.org/licenses/by-sa/3.0/
Latest update: Feb 27, 2013

3. Bubble Sort
氣泡排序法

4. Algorithm
1. 從第一個元素開始比較每一對相鄰元素
2. 若第一個元素大於第二個元素則交換
3. 每次遞減需要比較的元素對直到不需比
較

5. Origin
10 2 7 9 1
10 2 7 9 1

6. 1 st Iteration
10 2 7 9 1

7. 1 st Iteration
10 2 7 9 1

8. 1 st Iteration
2
10 2
10 7 9 1

9. 1 st Iteration
2
10 2
10 7 9 1

10. 1 st Iteration
2
10 2
7 7
10 9 1

11. 1 st Iteration
2
10 2
7 7
10 9 1

12. 1 st Iteration
2
10 2
7 7
9 9
10 1

13. 1 st Iteration
2
10 2
7 7
9 9
10 1

14. 1 st Iteration
2
10 2
7 7
9 1
9 1
10

15. 1 st Iteration
2 7 9 1 10
2
10 2
7 7
9 1
9 1
10

16. 2 nd Iteration
2 7 9 1 10

17. 2 nd Iteration
2 7 9 1 10

18. 2 nd Iteration
2 7 9 1 10

19. 2 nd Iteration
2 7 9 1 10

20. 2 nd Iteration
2 7 9 1 10

21. 2 nd Iteration
2 7 9 1 10

22. 2 nd Iteration
2 7 1
9 1
9 10

23. 2 nd Iteration
2 7 1 9 10
2 7 1
9 1
9 10

24. 3 rd Iteration
2 7 1 9 10

25. 3 rd Iteration
2 7 1 9 10

26. 3 rd Iteration
2 7 1 9 10

27. 3 rd Iteration
2 7 1 9 10

28. 3 rd Iteration
2 1
7 1
7 9 10

29. 3 rd Iteration
2 1 7 9 10
2 1
7 1
7 9 10

30. 4 th Iteration
2 1 7 9 10

31. 4 th Iteration
2 1 7 9 10

32. 4 th Iteration
1
2 1
2 7 9 10

33. 4 th Iteration
1 2 7 9 10
1
2 1
2 7 9 10

34. Result
1 2 7 9 10
1 2 7 9 10

35. Source Code
for ( int i = 0; i < n; ++i )
for ( int j = 0; j < n - 1 - i; ++j )
if ( A[ j ] > A[ j + 1 ] )
swap( A[ j ], A[ j + 1 ] );

36. Time Complexity
for ( int i = 0; i < n; ++i )
for ( int j = 0; j < n - 1 - i; ++j )
if ( A[ j ] > A[ j + 1 ] )
swap( A[ j ], A[ j + 1 ] );
最大循環次數略估
第 1 層迴圈 n
第 2 層迴圈 n

37. n×n= n 2
Time Complexity: O(n2)

38. 從範例中可發現...
耗費許多時間檢查有序數對

39. Merge Sort
合併排序法

40. Algorithm
採用 divide & conquer 策略

41. Divide
將當前數列對半切割遞迴進行
直到 剩一個元素

42. 2 9 4 3 8 7 5 1 6
2 9 4 3 8 7 5 1 6
2 9 4 3 8 7 5 1 6
2 9 4 3 8 7 5 1 6
2 9

43. Conquer
1. 利用兩個指標指向兩個有序數列 A 與 B
2. 比較指標指向的數值
3. 將較小的數值放入新的數列 C，並將該指標
指向下一數值
4. 直到某一指標指向數列結尾，將另一數列剩
餘的數值放都入數列 C

44. Merge Two Sequence
2 3 4 8 9 1 5 6 7

45. Merge Two Sequence
2 3 4 8 9 5 6 7
1

46. Merge Two Sequence
3 4 8 9 5 6 7
1 2

47. Merge Two Sequence
4 8 9 5 6 7
1 2 3

48. Merge Two Sequence
8 9 5 6 7
1 2 3 4

49. Merge Two Sequence
8 9 6 7
1 2 3 4 5

50. Merge Two Sequence
8 9 7
1 2 3 4 5 6

51. Merge Two Sequence
8 9
1 2 3 4 5 6 7

52. Merge Two Sequence
9
1 2 3 4 5 6 7 8

53. Merge Two Sequence
1 2 3 4 5 6 7 8 9

54. 1 2 3 4 5 6 7 8 9
2 3 4 8 9 1 5 6 7
2 4 9 3 8 5 7 1 6
2 9 4 3 8 7 5 1 6
2 9

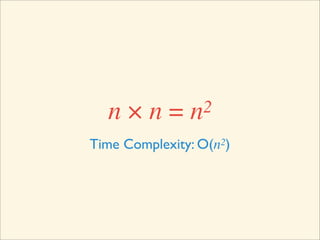
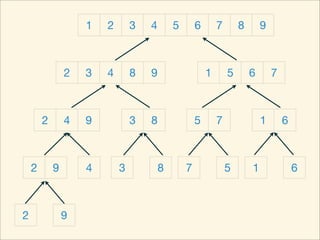
55. Source Code
int mergeSort( int L, int R ) {
if ( R - L == 1 )
return;
int mid = ( R + L ) / 2, C[ R - L ];
mergeSort( L, mid );
mergeSort( mid, R );
for ( int p1 = L, p2 = mid, p = 0; p < R - L; ++p ) {
if ( ( p1 != mid && A[ p1 ] < A[ p2 ] ) || p2 == R )
C[ p ] = A[ p1++ ];
else
C[ p ] = A[ p2++ ];
}
for ( int i = L; i < R; ++i )
A[ i ] = C[ i - L ];
}

56. Time Complexity
total time

57. Time Complexity
total time
n
2 * (n/2) = n
...
n * (n/n) = n

58. Best height
}
log2n

59. Time Complexity: O(nlog2n)

60. Quick Sort
快速排序法

61. Algorithm
採用 divide & conquer 策略

62. Divide
從數列中挑出一個元素作為 pivot，利
用 pivot 將原數列分為兩個子數列：
• 所有元素小於 pivot 的數列 A
• 所有元素大於 pivot 的元素的數列 B
• 等於 pivot 的元素可放置在任一個中

63. 2 9 4 3 8 7 5 1 6

64. 2 9 4 3 8 7 5 1 6

65. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8

66. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8

67. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6

68. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6

69. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6
2

70. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6
2

71. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6
2 5 6

72. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6
2 5 6

73. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6
2 5 6
5

74. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6
2 5 6
5

75. 2 9 4 3 8 7 5 1 6
2 4 3 5 1 6 9 8
2 1 4 5 6 9
2 5 6
5

76. Conquer
由於子數列已被 pivot 分為兩段，一段
小於等於 pivot 的數列 A，另一段大於
等於 pivot 的數列 B。

77. Conquer
由於子數列已被 pivot 分為兩段，一段
小於等於 pivot 的數列 A，另一段大於
等於 pivot 的數列 B。
A C B

78. 2

79. 1
2

80. 1 2
2

81. 1 2
2 6
5

82. 1 2
2 5 6
5

83. 1 2 4
2 5 6
5

84. 1 2 4 5 6
2 5 6
5

85. 3
1 2 4 5 6
2 5 6
5

86. 1 2 3 4 5 6
1 2 4 5 6
2 5 6
5

87. 1 2 3 4 5 6 8
1 2 4 5 6 9
2 5 6
5

88. 1 2 3 4 5 6 8 9
1 2 4 5 6 9
2 5 6
5

89. 7
1 2 3 4 5 6 8 9
1 2 4 5 6 9
2 5 6
5

90. 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 8 9
1 2 4 5 6 9
2 5 6
5

91. 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 8 9
1 2 4 5 6 9
2 5 6
5

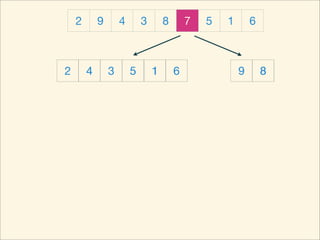
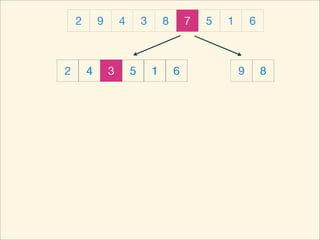
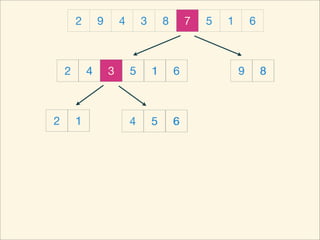
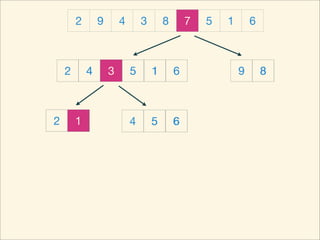
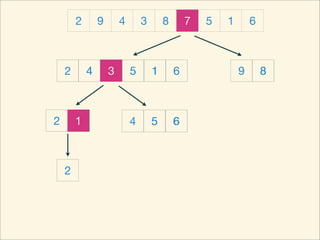
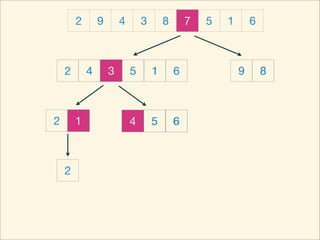
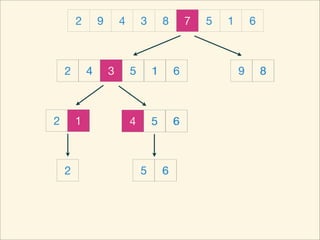
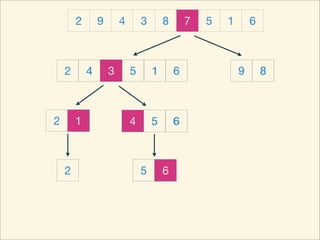
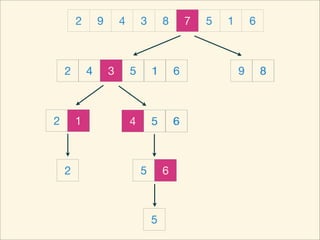
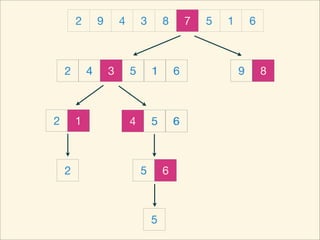
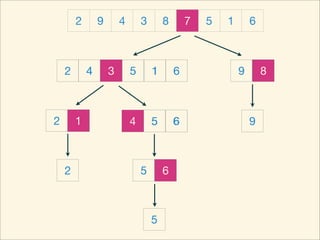
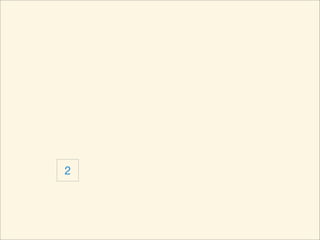
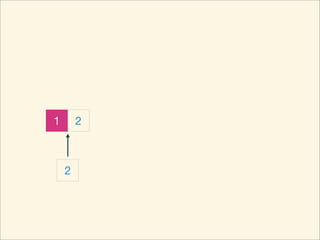
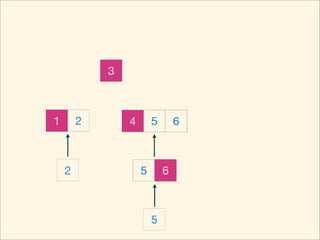
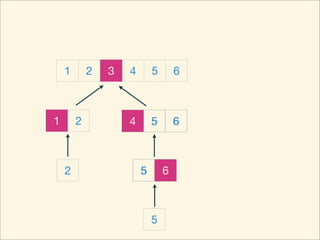
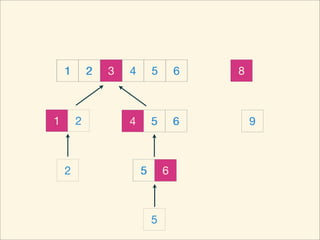
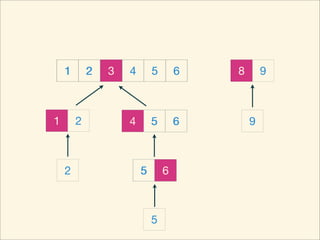
92. Source Code
void quickSort( int L, int R ) {
if ( R - L <= 1 )
return;
int pivot = N[ L ], p1 = L + 1, p2 = R - 1;
do {
while ( N[ p1++ ] <= pivot )
;
while ( N[ p2-- ] > pivot )
;
if ( p1 < p2 )
swap( N[ p1 ], N[ p2 ] );
} while ( p1 < p2 );
quickSort( L + 1, p1 );
quickSort( p1, R );
for ( int i = L + 1; i < p1; ++i )
swap( N[ i - 1 ], N[ i ] );
}

93. How to Divide
4 1 9 7 5 8 2 3 6

94. How to Divide
4 1 9 7 5 8 2 3 6

95. How to Divide
4 1 9 7 5 8 2 3 6

96. How to Divide
4 1 9 7 5 8 2 3 6

97. How to Divide
4 1 3 7 5 8 2 9 6

98. How to Divide
4 1 3 7 5 8 2 9 6

99. How to Divide
4 1 3 7 5 8 2 9 6

100. How to Divide
4 1 3 2 5 8 7 9 6

101. How to Divide
4 1 3 2 5 8 7 9 6

102. How to Divide
4 1 3 2 5 8 7 9 6

103. How to Divide
4 1 3 2 5 8 7 9 6
4 1 3 2 5 8 7 9 6

104. How to Conquer
4 1 2 3 5 6 7 8 9

105. How to Conquer
1 4 2 3 5 6 7 8 9

106. How to Conquer
1 2 4 3 5 6 7 8 9

107. How to Conquer
1 2 3 4 5 6 7 8 9

108. In-place Version
void quickSort( int L, int R ) {
if ( R - L <= 1 )
return;
int pivot = N[ R - 1 ], p = L;
for ( int i = L; i < R - 1; ++i ) {
if ( N[ i ] <= pivot ) {
swap( N[ i ], N[ p ] );
++p;
}
}
swap( N[ R - 1 ], N[ p ] );
quickSort( L, p );
quickSort( p + 1, R );
}

109. How to Divide
2 9 4 3 8 7 5 1 6

110. How to Divide
2 9 4 3 8 7 5 1 6

111. How to Divide
2 9 4 3 8 7 5 1 6

112. How to Divide
2 9 4 3 8 7 5 1 6

113. How to Divide
2 9 4 3 8 7 5 1 6

114. How to Divide
2 9 4 3 8 7 5 1 6

115. How to Divide
2 9 4 3 8 7 5 1 6

116. How to Divide
2 4
9 9
4 3 8 7 5 1 6

117. How to Divide
2 4
9 9
4 3 8 7 5 1 6

118. How to Divide
2 4
9 9
4 3 8 7 5 1 6

119. How to Divide
2 4
9 3
4 9
3 8 7 5 1 6

120. How to Divide
2 4
9 3
4 9
3 8 7 5 1 6

121. How to Divide
2 4
9 3
4 9
3 8 7 5 1 6

122. How to Divide
2 4
9 3
4 9
3 8 7 5 1 6

123. How to Divide
2 4
9 3
4 9
3 8 7 5 1 6

124. How to Divide
2 4
9 3
4 9
3 8 7 5 1 6

125. How to Divide
2 4
9 3
4 9
3 8 7 5 1 6

126. How to Divide
2 4
9 3
4 5
3 8 7 9
5 1 6

127. How to Divide
2 4
9 3
4 5
3 8 7 9
5 1 6

128. How to Divide
2 4
9 3
4 5
3 8 7 9
5 1 6

129. How to Divide
2 4
9 3
4 5
3 8
1 7 9
5 8
1 6

130. How to Divide
2 4
9 3
4 5
3 1
8 7 9
5 8
1 6

131. How to Divide
2 4
9 3
4 5
3 1
8 6
7 9
5 8
1 7
6

132. How to Divide
2 4
9 3
4 5
3 1
8 6
7 9
5 8
1 7
6
2 4 3 5 1 9 8 7

133. How to Conquer
6
1 2 3 4 5 7 8 9

134. How to Conquer
1 2 3 4 5 6 7 8 9
1 2 3 4 5 7 8 9

135. Time Complexity
total time

136. Time Complexity
total time
n
2 * (n/2) = n
...
n * (n/n) = n

137. Best height
}
log2n

138. Worst height
}
n

139. Time Complexity:
O(nlog2n) ~ O(n 2)

140. Average Time Complexity:
O(nlog2n)

141. Builtin Function
如果你純粹想要排序罷了...

142. qsort (C/C++)
• include <stdlib.h> or <cstdlib>
• compare function
void qsort (void* base, size_t num, size_t
size, int (*compar)(const void*,const void*));

143. void qsort (void* base, size_t num, size_t
size, int (*compar)(const void*,const void*));
base: 指向欲排序列表起始位置之指標
num: 欲排序的元素數量
size: 各元素大小
compar: 比較函式的函式指標

144. Compare Function
Function prototype:
int function_name(const void* p1, const void* p2);
return value means
less than 0 p1 < p2
equal to 0 p1 == p2
greater than 0 p1 > p2

145. Example
int cmp( const void* p1, const void* p2 ) {
return *(int*)p1 - *(int*)p2;
}
int main() {
int n, N[ 10010 ];
while ( scanf( “%d”, &n ) != EOF ) {
int x;
for ( int i = 0; i < n; ++i ) {
scanf( “%d”, &x );
N[ i ] = x;
}
qsort( N, n, sizeof( int ), cmp );
}
return 0;
}

146. sort (STL)
• include <algorithm>
• compare function for customized
behavior
template <class RandomAccessIterator>
void sort (RandomAccessIterator first,
RandomAccessIterator last);
template <class RandomAccessIterator, class Compare>
void sort (RandomAccessIterator first,
RandomAccessIterator last, Compare comp);

147. Sort by operator <
template <class RandomAccessIterator>
void sort (RandomAccessIterator first,
RandomAccessIterator last);
first: 指向欲排序列表起始位置之 iterator
last: 指向欲排序列表結尾位置之 iterator
指標可被轉型為 iterator!
依照該資料型別的小於運算子 (<) 作為排序依據！

148. Customized Data Type
Function prototype for operator <:
bool operator< ( const type_name &p ) const;
return value means
TRUE this < p
FALSE this >= p

149. Example (builtin type)
int main() {
int n, N[ 10010 ];
while ( scanf( “%d”, &n ) != EOF ) {
int x;
for ( int i = 0; i < n; ++i ) {
scanf( “%d”, &x );
N[ i ] = x;
}
sort( N, N + n );
}
return 0;
}

150. Example (custom type)
struct T {
int x, y;
bool operator< ( const T &p ) const {
return x == p.x ? x < p.x : y < p.y;
}
};
T pt[ 10010 ];
int main() {
int n;
while ( scanf( “%d”, &n ) != EOF ) {
int x, y;
for ( int i = 0; i < n; ++i ) {
scanf( “%d %d”, &x, &y );
pt[ i ].x = x, pt[ i ].y = y;
}
sort( pt, pt + n );
}
return 0;
}

151. Sort by Compare Function
template <class RandomAccessIterator, class Compare>
void sort (RandomAccessIterator first,
RandomAccessIterator last, Compare comp);
first: 指向欲排序列表起始位置之 iterator
last: 指向欲排序列表結尾位置之 iterator
comp: 比較函式
指標可被轉型為 iterator!

152. Customized Data Type
Function prototyp:
bool function_name ( type_name p1, type_name p2 );
return value means
TRUE p1 < p2
FALSE p1 >= p2

153. Example (descending)
bool descending( int p1, int p2 ) {
return p1 >= p2;
}
int main() {
int n, N[ 10010 ];
while ( scanf( “%d”, &n ) != EOF ) {
int x;
for ( int i = 0; i < n; ++i ) {
scanf( “%d”, &x );
N[ i ] = x;
}
sort( N, N + n, descending );
}
return 0;
}

154. Reference
• 冒泡排序 - 維基百科，自由的百科全書
• 歸併排序 - 維基百科，自由的百科全書
• 快速排序 - 維基百科，自由的百科全書
• qsort - C++ Reference
• sort - C++ Reference

155. Practice Now
10810 - Ultra-QuickSort

156. Thank You for Your
Listening.