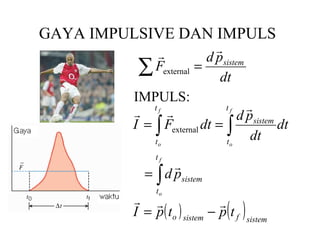
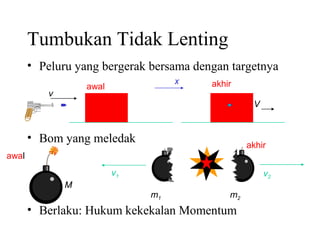
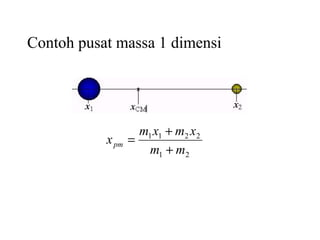
Dokumen ini membahas konsep momentum linier, impuls, serta hukum kekekalan momentum. Terdapat penjelasan mengenai gaya dan interaksi antara partikel, serta pengelompokan tumbukan seperti lenting sempurna dan tidak lenting. Selain itu, dokumen juga menyertakan contoh pusat massa dalam sistem yang terdiri dari beberapa benda.

1. MOMENTUM LINIER
DAN IMPULS

2. • Gaya fungsi dari waktu  Konsep
Momentum
• Momentum  perubahan yang terjadi
akibat adanya interaksi antara masing-
masing partikel

3. MOMENTUM LINIER
Hukum II Newton
Untuk m konstan, diperoleh
bentuk hukum II Newton
yang dikenal pada dinamika
Definisi momentum linier vmp

=
v
dt
dm
dt
vd
m
dt
vdm
dt
pd
F



+=
==∑
am
dt
vd
mF


==∑
F


4. KEKEKALAN MOMENTUM LINIER
Untuk sistem dengan:
Gaya total pada sistem: ∑∑∑ += externalinternal FFF

0internal =∑F

Maka momentum sistem :
∑= externalF
dt
pd sistem

Jika 00external =⇒=∑ dt
pd
F sistem

sistemakhirsistemawalsistem pppd

=⇒= Konstan

5. GAYA IMPULSIVE DAN IMPULS
IMPULS:
dt
pd
F sistem

=∑ external
( ) ( )sistemfsistemo
t
t
sistem
t
t
sistem
t
t
tptpI
pd
dt
dt
pd
dtFI
f
o
f
o
f
o



−=
=
==
∫
∫∫ external

6. DESKRIPSI GRAFIK
Grafik gaya dari pemukul kepada sebuah bola dan
momentum bola selama menerima gaya.
Fres (N)
Luas = Fres t = Impuls
t (detik)
P = mv (kg m/s)
t (detik)
tan α = ∆p/∆t = Fres

7. TUMBUKAN

8. PENGELOMPOKAN TUMBUKAN
• Lenting sempurna
• Lenting sebagian
• Tidak lenting sama
sekali
• Energi kinetik sistem
konstan
• Energi kinetik sistem tidak
konstan, tetapi berkurang
• Benda bergerak bersama
setelah tumbukan. Energi
kinetik sistem berkurang

9. Tumbukan Lenting Sempurna
• Tumbukan antara dua buah benda, dimana
diantaranya terdapat pegas:
• Tumbukan bola pada permainan billiard
• Berlaku: Hukum kekekalan Momentum dan
Hukum kekekalan Energi
vvi

10. Tumbukan Tidak Lenting
• Peluru yang bergerak bersama dengan targetnya
• Bom yang meledak
• Berlaku: Hukum kekekalan Momentum
v
V
awal akhirx
M
awal
m1 m2
v1 v2
akhir

11. Pusat Massa
∑∑ ==
i
i
i
i
eksternaltotal
dt
rd
mFF 2
2 
2
2
2
2
2
2
2
2
dt
Rd
MF
M
rm
dt
d
M
dt
rmd
dt
rmd
F
total
iiii
i
ii
total


=








===
∑∑∑
M
rm
R ii∑=


Sistem yang terdiri dari n buah benda, maka:
Dimana:
Adalah pusat massa dari sistem
tersebut

12. Contoh pusat massa 1 dimensi
21
2211
mm
xmxm
xpm
+
+
=