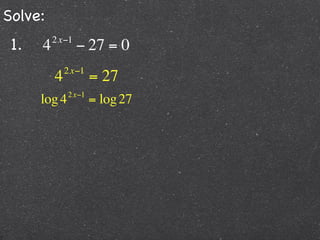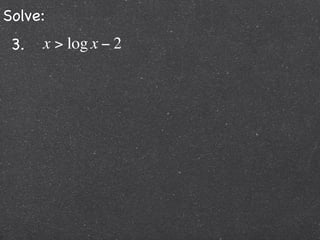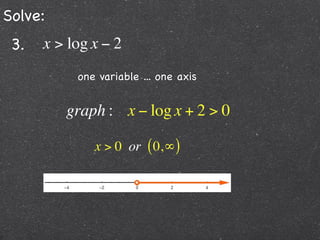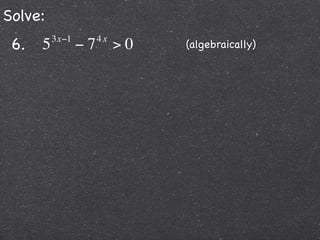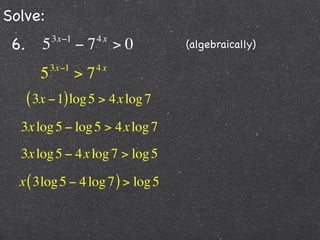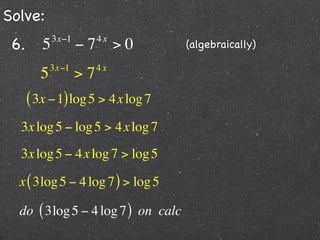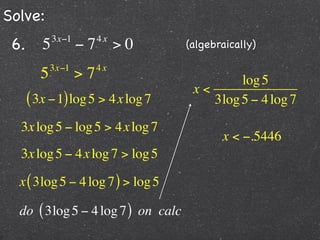This document contains step-by-step solutions to 6 exponential and logarithmic equations. The solutions involve algebraic manipulation of logarithmic and exponential terms as well as graphical methods. Scriptural context is provided at the beginning emphasizing the instructional value of studying such examples.

1. 4.4 Exponential &
Logarithmic Equations
Day 2
Romans 15:4 For whatever was written in former
days was written for our instruction, that through
endurance and through the encouragement of the
Scriptures we might have hope.

2. Solve:
1. 4 2 x−1
− 27 = 0

3. Solve:
1. 4 2 x−1
− 27 = 0
2 x−1
4 = 27

4. Solve:
1. 4 2 x−1
− 27 = 0
2 x−1
4 = 27
2 x−1
log 4 = log 27

5. Solve:
1. 4 2 x−1
− 27 = 0
2 x−1
4 = 27
2 x−1
log 4 = log 27
( 2x − 1) log 4 = log 27

6. Solve:
1. 4 2 x−1
− 27 = 0
2 x−1
4 = 27
2 x−1
log 4 = log 27
( 2x − 1) log 4 = log 27
log 27
2x − 1 =
log 4

7. Solve:
1. 4 2 x−1
− 27 = 0
2 x−1
4 = 27
2 x−1
log 4 = log 27
( 2x − 1) log 4 = log 27
log 27
2x − 1 =
log 4
log 27
2x = +1
log 4

8. Solve:
1. 4 2 x−1
− 27 = 0
2 x−1
4 = 27 log 27 1
log 4 2 x−1
= log 27 x= +
2 log 4 2
( 2x − 1) log 4 = log 27 this is now
log 27 “calculator ready”
2x − 1 =
log 4
log 27
2x = +1
log 4

9. Solve:
1. 4 2 x−1
− 27 = 0
2 x−1
4 = 27 log 27 1
log 4 2 x−1
= log 27 x= +
2 log 4 2
( 2x − 1) log 4 = log 27 this is now
log 27 “calculator ready”
2x − 1 =
log 4 x ≈ 1.6887
log 27
2x = +1
log 4

10. Solve:
2. e = x − 1
x 2

11. Solve:
2. e = x − 1
x 2
no algebraic method presents itself ...
do graphically

12. Solve:
2. e = x − 1
x 2
no algebraic method presents itself ...
do graphically
x 2
y1 = e y2 = x − 1

13. Solve:
2. e = x − 1
x 2
no algebraic method presents itself ...
do graphically
x 2
y1 = e y2 = x − 1
find intersection points

14. Solve:
2. e = x − 1
x 2
no algebraic method presents itself ...
do graphically
x 2
y1 = e y2 = x − 1
find intersection points
x ≈ −1.1478

15. Solve:
3. x > log x − 2

16. Solve:
3. x > log x − 2
one variable ... one axis

17. Solve:
3. x > log x − 2
one variable ... one axis
graph : x − log x + 2 > 0

18. Solve:
3. x > log x − 2
one variable ... one axis
graph : x − log x + 2 > 0
x > 0 or ( 0,∞ )

19. Solve:
4. y < log ( 2x ) + 1

20. Solve:
4. y < log ( 2x ) + 1
two variables ... two axes
graph on graph paper!

21. Solve:
4. y < log ( 2x ) + 1
two variables ... two axes
graph on graph paper!
graph : y1 = log ( 2x ) + 1
dotted line & shade below

22. Solve:
5. x
y≥e −2

23. Solve:
5. x
y≥e −2
two variables ... two axes
graph on graph paper!

24. Solve:
5. x
y≥e −2
two variables ... two axes
graph on graph paper!
x
graph : y1 = e − 2
solid line & shade above

25. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)

26. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7

27. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7
( 3x − 1) log 5 > 4x log 7

28. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7
( 3x − 1) log 5 > 4x log 7
3x log 5 − log 5 > 4x log 7

29. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7
( 3x − 1) log 5 > 4x log 7
3x log 5 − log 5 > 4x log 7
3x log 5 − 4x log 7 > log 5

30. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7
( 3x − 1) log 5 > 4x log 7
3x log 5 − log 5 > 4x log 7
3x log 5 − 4x log 7 > log 5
x ( 3log 5 − 4 log 7 ) > log 5

31. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7
( 3x − 1) log 5 > 4x log 7
3x log 5 − log 5 > 4x log 7
3x log 5 − 4x log 7 > log 5
x ( 3log 5 − 4 log 7 ) > log 5
do ( 3log 5 − 4 log 7 ) on calc

32. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7 log 5
x<
( 3x − 1) log 5 > 4x log 7 3log 5 − 4 log 7
3x log 5 − log 5 > 4x log 7
3x log 5 − 4x log 7 > log 5
x ( 3log 5 − 4 log 7 ) > log 5
do ( 3log 5 − 4 log 7 ) on calc

33. Solve:
6. 5 3x−1
−7 4x
>0 (algebraically)
3x−1 4x
5 >7 log 5
x<
( 3x − 1) log 5 > 4x log 7 3log 5 − 4 log 7
3x log 5 − log 5 > 4x log 7
x < −.5446
3x log 5 − 4x log 7 > log 5
x ( 3log 5 − 4 log 7 ) > log 5
do ( 3log 5 − 4 log 7 ) on calc

34. HW #7
It is time for us all to stand and cheer for the doer,
the achiever – the one who recognizes the challenge
and does something about it.
Vince Lombardi