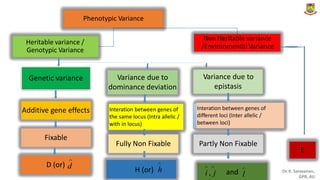
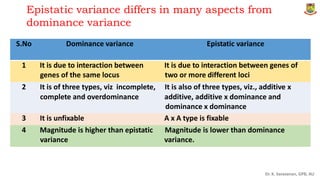
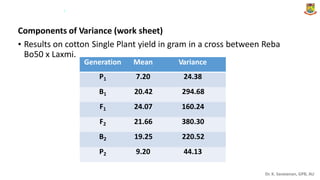
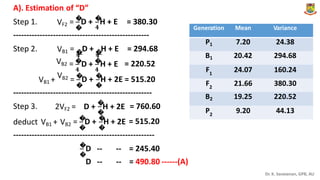
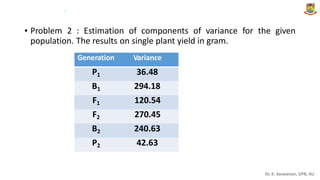
The document discusses the components of variance and gene action in quantitative genetics, emphasizing the importance of genetic variability for plant breeding. It categorizes variance into phenotypic, genotypic, and environmental, detailing their significance and the implications of different types of gene action. The document also outlines methodologies for estimating these variances and how they relate to breeding strategies for self-pollinated and cross-pollinated crops.