NIPS Reading Group

1. Temporal Difference Models: Model-Free
Deep RL for Model-Based Control
V. Pong*, S. Gu*, M. Dalal, and S. Levine
ICLR 2018
Eiji Uchibe
Dept. of Brain Robot Interface, ATR Computational Neuroscience Labs.

2. 論文の概要と選択理由
• モデルフリーRLとモデルベースRLの共同
• モデルベースの利点は仮想経験の生成だけでなく
プランニングが利用できる点
• Monte Carlo Tree Searchなどの方法がロボット制御
問題では長期予測の点から役に立たない
• モデル予測制御における制約条件の工夫により解決
[O'Doherty et al., 2017]

3. モデルベース強化学習
• 狭義には状態遷移確率𝑃(𝑠′ ∣ 𝑠, 𝑎)が既知、もしくは推定した
モデルを用いた強化学習アルゴリズム
– 価値反復法や方策反復法、
PILCO [Deisenroth et al., 2014], MCTSなど
環境𝑃 𝑠′ 𝑠, 𝑎
観測𝑜
行動𝑎
報酬𝑟内部状態𝑠
学習率 𝛼
逆温度 𝛽
割引率 𝛾

4. 最近のモデルベース・モデルフリー強化学習
S. GuのICLR2017のスライドから引用

5. 𝑠 𝑔
目標条件付き価値関数 (Goal-conditioned value function)
• 価値関数を目標状態𝑠 𝑔 ∈ 𝒢にも依存するように拡張
マルチタスク強化学習
• 基本的には通常の状態行動価値関数を
と拡張するだけ
• タスクを失敗しても𝑠 𝑔を失敗した軌道の中から選び直すことで
非零の報酬を生成し学習する [Andrychowicz et al., 2017]
𝑄(𝑠, 𝑎, 𝑠 𝑔)
𝑠𝑡
𝑎 𝑡
𝑠𝑡+1
𝑠 𝑔
𝑠 𝑔

6. モデル予測制御 (Model Predictive Control)
• 状態のダイナミクスは既知
• モデルベース強化学習とみなせる
• 目的
制約条件
• 各時間で制約付き最適化問題
を解くので、計算コストは高い
𝑎 𝑡 = argmax
𝑎 𝑡:𝑡+𝑇
෍
𝑖=𝑡
𝑡+𝑇
𝑟𝑐(𝑠𝑖, 𝑎𝑖)
𝑠𝑖+1 = 𝑓 𝑠𝑖, 𝑎𝑖 , ∀𝑖 ∈ 𝑡, … , 𝑡 + 𝑇 − 1
[山田2006]から引用

7. 目標条件付き価値関数からモデルへ
• 目標集合𝒢が状態集合𝒮と同じ場合(𝒢 = 𝒮)を考える
• 距離ベース報酬関数を導入する
• 割引率𝛾 = 0のとき価値関数は即時報酬に収束
– 𝐷は距離関数なので、𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔 = 0なら𝑠𝑡+1 = 𝑠𝑔を意味する
• モデル予測制御の制約条件を変更
𝑟𝑑 𝑠𝑡, 𝑎 𝑡, 𝑠𝑡+1, 𝑠 𝑔 = −𝐷 𝑠𝑡+1, 𝑠 𝑔
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔 = −𝐷 𝑠𝑡+1, 𝑠 𝑔
𝑎 𝑡 = argmax
𝑎 𝑡:𝑡+𝑇
෍
𝑖=𝑡
𝑡+𝑇
𝑟𝑐(𝑠𝑖, 𝑎𝑖)
𝑠𝑖+1 = 𝑓 𝑠𝑖, 𝑎𝑖 , ∀𝑖 ∈ 𝑡, … , 𝑡 + 𝑇 − 1
𝑎 𝑡 = argmax
𝑎 𝑡:𝑡+𝑇,𝑠 𝑡+1:𝑡+𝑇
෍
𝑖=𝑡
𝑡+𝑇
𝑟𝑐(𝑠𝑖, 𝑎𝑖)
𝑄 𝑠𝑖, 𝑎𝑖, 𝑠𝑖+1 = 0, ∀𝑖 ∈ 𝑡, … , 𝑡 + 𝑇 − 1
この段階では、表現方法が
違うだけで同じことを計算

8. Temporal Difference Modelによる長期予測学習
• 𝛾 > 0の場合、𝑄(𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔) が何を意味するか明確でない
• infinite horizon discount rewardではなく、finite horizon total reward
で定式化すれば良さそう
• 決定論的な状態遷移の場合
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔, 𝜏 = ቐ
−𝐷(𝑠𝑡+1, 𝑠 𝑔) 𝜏 = 0
max
𝑎
𝑄 𝑠𝑡+1, 𝑎, 𝑠 𝑔, 𝜏 − 1 𝜏 ≠ 0
𝑠𝑡
𝑎 𝑡
𝑠𝑡+1
𝑠 𝑔
𝑠𝑡+𝜏+1
∗
𝜋∗
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔, 𝜏
状態𝑠𝑡で行動𝑎 𝑡を実行し
状態𝑠𝑡+1に遷移し、以降
𝜏ステップ最適方策𝜋∗
に
従って行動して、𝑠𝑡+𝜏+1
∗
に遷移する

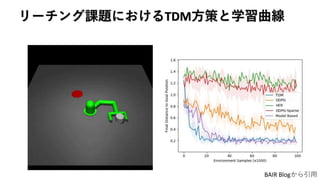
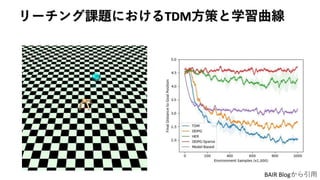
9. TDMと通常のfinite horizon total rewardの比較
• TDM
• Finite horizon total reward
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔, 𝜏 = 𝔼 𝑝 𝑠𝑡+1 𝑠𝑡, 𝑎 𝑡
ൣ−𝐷 𝑠𝑡+1, 𝑠 𝑔 𝕀 𝜏 = 0
቉+ max
𝑎
𝑄 𝑠𝑡+1, 𝑎, 𝑠 𝑔, 𝜏 − 1 𝕀 𝜏 ≠ 0
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑡 = 𝔼 𝑝 𝑠𝑡+1 𝑠𝑡, 𝑎 𝑡
𝑟 𝑠𝑡, 𝑎 𝑡, 𝑠𝑡+1 + max
𝑎
𝑄 𝑠𝑡+1, 𝑎, 𝑡 + 1

10. 行動の決定 (Model Predictive Control)
• 各時刻で以下の制約付き最適化問題を解く
– 計算を簡略化するために𝐾ステップごとの評価を用いる
– さらに𝐾 = 𝑇として簡略化した場合
𝑎 𝑡 = argmax
𝑎 𝑡:𝐾:𝑡+𝑇,𝑠 𝑡+𝐾:𝐾:𝑡+𝑇
෍
𝑖=𝑡,𝑡+𝐾,…,𝑡+𝑇
𝑟𝑐(𝑠𝑖, 𝑎𝑖)
s.t. 𝑄 𝑠𝑖, 𝑎𝑖, 𝑠𝑖+𝐾, 𝐾 − 1 = 0 ∀ 𝑖 ∈ 𝑡, 𝑡 + 𝐾, … , 𝑡 + 𝑇 − 𝐾
𝑎 𝑡 = argmax
𝑎 𝑡,𝑎 𝑡+𝑇,𝑠 𝑡+𝑇
𝑟𝑐 𝑠𝑡+𝑇, 𝑎 𝑡+𝑇 s.t. 𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠𝑡+𝑇, 𝑇 − 1 = 0

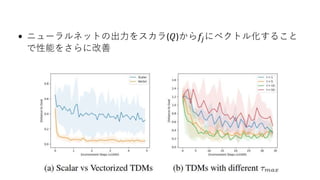
11. 価値関数を構造化した場合の行動の決定
• 前述の制約付き最適化問題を各時刻で解くのは大変
• 価値関数の表現を限定
– 𝑓をニューラルネットなどで近似する
• 制約付き最適化が制約なし最適化問題に帰着
– タスクが目標状態𝑠𝑔に到達するようなケースの場合
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔, 𝜏 = −𝐷 𝑓 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔, 𝜏 , 𝑠 𝑔 𝑄が非負であることを保証
𝑎 𝑡 = argmax
𝑎 𝑡,𝑎 𝑡+𝑇,𝑠 𝑡+𝑇
𝑟𝑐 𝑓 𝑠𝑡, 𝑎 𝑡, 𝑠𝑡+𝑇, 𝑇 − 1 , 𝑎 𝑡+𝑇
𝑎 𝑡 = argmax
𝑎
𝑄 𝑠𝑡, 𝑎, 𝑠 𝑔, 𝑇

13. リーチング課題におけるTDM方策と学習曲線
BAIR Blogから引用

14. リーチング課題におけるTDM方策と学習曲線
BAIR Blogから引用

16. • ニューラルネットの出力をスカラ(𝑄)から𝑓𝑗にベクトル化すること
で性能をさらに改善

17. 個人的な意見
• モデルを使ったプランニングを制約条件の形でMPCに導入するの
は興味深い
• 𝑄(𝑠, 𝑎, 𝑠 𝑔, 𝜏)の学習は大変そうで、結果として正しく学習できてい
るのか確認したい
• 状態空間上での距離関数𝐷(𝑠, 𝑠 𝑔)と𝑠から𝑠 𝑔に遷移するのに必要な
ステップ数は異なるので、最小ステップを学習するような定式化
はどうか
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔, 𝜏 = 𝔼 𝑝 𝑠𝑡+1 𝑠𝑡, 𝑎 𝑡
1 + min
𝑎
𝑄 𝑠𝑡+1, 𝑎, 𝑠 𝑔, 𝜏 − 1
𝑄 𝑠𝑡, 𝑎 𝑡, 𝑠 𝑔, 0 = 𝐷 𝑠𝑡+1, 𝑠 𝑔 or +∞

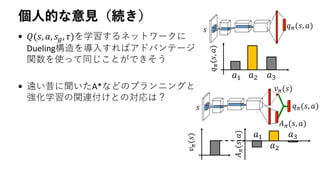
18. 個人的な意見（続き）
• 𝑄(𝑠, 𝑎, 𝑠 𝑔, 𝜏)を学習するネットワークに
Dueling構造を導入すればアドバンテージ
関数を使って同じことができそう
• 遠い昔に聞いたA*などのプランニングと
強化学習の関連付けとの対応は？
𝑠 𝑞 𝜋(𝑠, 𝑎)
𝑎1 𝑎2 𝑎3
𝑞𝜋(𝑠,𝑎)
𝑠 𝑞 𝜋(𝑠, 𝑎)
𝑣 𝜋(𝑠)
𝐴 𝜋(𝑠, 𝑎)
𝑎1
𝑎2
𝑎3
𝐴𝜋(𝑠,𝑎)
𝑣𝜋(𝑠)

19. References
• Andrychowicz, M., …, Abbeel, P., and Zaremba, W. (2017). Hindsight experience replay. NIPS 30.
• O'Doherty, J.P., Cockburn, J., and Pauli, W. M. (2017). Learning, Reward, and Decision Making. Annual
Review of Psychology, 68:73-100.
• Pong*, V., Gu*, S., Dalal, M., and Levine, S. (2018). Temporal Difference Models: Model-Free Deep RL
for Model-Based Control. In Proc. of ICLR 2018.
• Pong, V. TDM: From Model-Free to Model-Based Deep Reinforcement Learning. BAIR Blog.
• 山田照樹. モデル予測制御理論の紹介. SICEセミナー, 2006.