「これからの強化学習」勉強会#2

1. 「これからの強化学習」勉強会#2
テキスト
これからの強化学習
牧野 貴樹 澁谷 長史 白川 真一 浅田 稔 麻生 英樹 荒井 幸代 飯間 等 伊藤 真
大倉 和博 黒江 康明 杉本 徳和 坪井 祐太 銅谷 賢治 前田 新一 松井 藤五郎
南 泰浩 宮崎 和光 目黒 豊美 森村 哲郎 森本 淳 保田 俊行 吉本 潤一郎
森北出版 2016-10-27
Amazonで詳しく見る by G-Tools
今回の範囲
第1章 強化学習の基礎的理論 ―― 1.4節～1.5節
第2章 強化学習の発展的理論
第3章 強化学習の工学応用
第4章 知能のモデルとしての強化学習
2017/01/02 Chihiro Kusunoki

2. その他の参考文献
強化学習
Richard S.Sutton Andrew G.Barto 三上 貞芳 皆川 雅章
森北出版 2000-12-01
Amazonで詳しく見る by G-Tools
目次
方策勾配による解法
REINFORCE アルゴリズム
アクター・クリティック手法
POMDP

3. 前回までのあらすじ
強化学習問題を解く（ ⇔ 最適方策 π* を求める ）には、最適行動
価値関数 Q* を解けばよい（ or 数値的に推定すればよい ）。
→ ただし、前回までの解法だと状態集合や行動集合が連続的なとき困る。
連続的だと評価・改善対象の π(a|s)，Q(s, a) を配列で表現できず
サンプルエピソード生成や逐次近似による Q* の推定ができない。
そのような場合そもそも π* の存在も保証されていない（要出典）。
• 状態集合や行動集合が離散集合でない例：
‐ 空の色を見て（状態）、再現すべく絵の具を混ぜる（行動）。
※ 空の色をデジカメで取り込む場合は、状態は離散的かもしれない。
‐ 川の流れの向きと速さを検知して（状態）、最短距離で対岸に
着くようにラジコンボートの舵を制御する（行動）。
※ センサやアクチュエータによっては離散的かもしれない。
‐ ギョウザの味をみて（状態）、満足度が高くなるような比率で
酢・醤油・ラー油を混ぜる（行動）。
※ 満足度を数値化するメカニズムは謎。

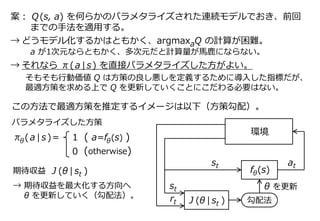
4. 案： Q(s, a) を何らかのパラメタライズされた連続モデルでおき、前回
までの手法を適用する。
→ どうモデル化するかはともかく、argmaxaQ の計算が困難。
a が1次元ならともかく、多次元だと計算量が馬鹿にならない。
→ それなら π(a|s) を直接パラメタライズした方がよい。
そもそも行動価値 Q は方策の良し悪しを定義するために導入した指標だが、
最適方策を求める上で Q を更新していくことにこだわる必要はない。
st
π (a|s)＝ 1 ( a=f (s) )θ θ
0 (otherwise)
f (s)θ
at
環境
rt
st
J (θ | st )
θ を更新
勾配法
この方法で最適方策を推定するイメージは以下（方策勾配）。
パラメタライズした方策
期待収益
→ 期待収益を最大化する方向へ
θ を更新していく（勾配法）。
J (θ | st )

5. 方策勾配による解法
方策 π をパラメタライズされたモデル化し、直接改善する作戦。
…といってもどのようなモデルにすればいいのか → とりあえず状態 s を
代入したら、取るべき行動 a の確率分布を返してくれればよい。
π (a|s)＝softmax(θ )θ s a
θ =1手目
「1六歩」の価値
「2六歩」の価値
「3六歩」の価値
「6八飛」の価値
「7八飛」の価値
π (a|s)＝softmax(θ Φ(s,a’))θ a
T
① 状態も行動も離散的
② 行動のみ離散的
③ 状態も行動も連続的 π (a|s)＝N(Ws ,C)θ ※ d 次元正規分布
例えば、機械学習でおなじみの確率分布：
① のイメージ
赤字が最適化対象パラメータ
a

6. 眠さ
ストレス
② のイメージ
Φ(今日の体調, コーヒー銘柄) =
感じる苦味
感じる酸味
感じるコク
A = {モカ, キリマンジャロ, ブルーマウンテン, グァテマラ}
θ =
苦味の価値
酸味の価値
コクの価値
※ あくまで模式的な例。
※ 特徴ベクトル Φ の
各要素に「苦味」
「酸味」「コク」
のような意味がある
とは限らない。
③ のイメージ
A =
※ あくまで模式的な例。
S = {今日の体調 | 今日の体調 ∈ Rd }
コーヒー濃さ
砂糖の量
ミルクの量
a= a ∈ R3
S = s= s ∈ R2
Ws =
眠さ
ストレス
w11
w21
w31
w12
w22
w32
θ Φ(今日の体調, コーヒー銘柄) ＝
T 今日の体調の下での
コーヒー銘柄の価値
最適な濃さ
最適な砂糖量
最適な牛乳量
=
w11= 単位眠さあたり必要なコーヒー濃さ
c11
c21
c31
c12
c22
c32
c13
c23
c33
C =
c22 = 砂糖量に許容
される誤差
c23 = c32 = 砂糖とミルクの間の束縛条件

7. あとは期待収益 J (θ | st ) の θ 勾配方向に θ を更新していけばよい。
θt+1 ← θt + η∇ J (θ | st )
更新時の学習率 η は、一般的な機械学習の手法よろしく頑張って決める。
勾配 ∇ J (θ | st ) の理論式と導出は論文参照。
→ ただし、上の理論式は解析的に求まるとは限らない & 表式に Q が含
まれており、環境のダイナミクスが既知であることを前提とする。
→ 前回のモンテカルロ法や Sarsa / Q学習のように、観測データを利用し
ていくアルゴリズムが望ましい。
θ
R. S. Sutton, D. A. McAllester, S. P. Singh, and Y. Mansour: Policy Gradient
Methods for Reinforcement Learning with Function Approximation, Advances in
Neural Information Processing Systems 12, pp. 1057-1063 (2000).
https://webdocs.cs.ualberta.ca/~sutton/papers/SMSM-NIPS99.pdf
π
θ

8. 方策勾配による解法1. REINFORCE アルゴリズム
勾配を求めるため、勾配の表式に含まれる Q を観測データで近似したい。
Q (st , at) は「方策πの下での状態行動対 (st , at) の価値 ≡ 状態 st の
ときに行動 at を選択し、その後は方策 π にしたがうときの期待収益」
なので、ものすごく粗っぽく考えれば、π にしたがって生成したエピ
ソード中で st にたどり着いたときに得た報酬 rt で置き換えられる（即時
報酬 rt こそが、方策 π の下での st の価値と考える）。
→ 実際にこの粗い近似で解くのが REINFORCE アルゴリズム。
π
π
R. J. Williams: Simple Statistical Gradient-Following Algorithms for Connectionist
Reinforcement Learning, Machine Learning, Vol. 8, Issue 3, pp. 229-256 (1992).
http://www-anw.cs.umass.edu/~barto/courses/cs687/williams92simple.pdf
ちなみに、REINFORCE は以下の略だそうです（論文参照）。
Δθ = α × (r － b) × ∇ log(π)
REward
Increment
即時報酬に
よる θ 修正分
Nonnegative
Factor
非負の学習率
Offset
Reinforcement
オフセット済
即時報酬
Characteristic
Eligibility
現在の θ の
適格度
θ ※ b は勾配の推定
分散を小さくす
るために導入す
るベースライン。

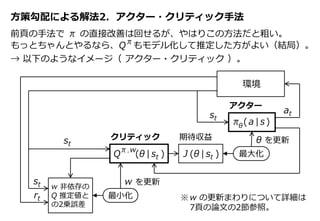
9. 方策勾配による解法2. アクター・クリティック手法
前頁の手法で π の直接改善は回せるが、やはりこの方法だと粗い。
もっとちゃんとやるなら、Q もモデル化して推定した方がよい（結局）。
st
at
環境
rt
st
J (θ | st )
θ を更新
最大化
π,w
Q (θ | st )
π (a|s)θ
アクター
クリティック 期待収益
w を更新
最小化
st
π
→ 以下のようなイメージ（ アクター・クリティック ）。
w 非依存の
Q 推定値と
の2乗誤差
※w の更新まわりについて詳細は
7頁の論文の2節参照。

10. アクター（行動器）＝ 推定方策： 行動を決定する。
クリティック（評価器）＝ 推定価値関数： 行動の結果を評価する。
前頁の図のようなサイクルを組めば、方策勾配による π の改善が回せる。
ここで疑問： θ 空間における勾配方向に θ を更新するのでいいのか。
最終目標は π を最もよい方策にしてくれる θ を見つけることだった。
→ θ 空間において勾配をみてその方向に θ 動かすより、π がよくなる
ような方向に動かす方がよいのでは。
→ 確率分布間の距離はカルバック・ライブラー情報量という指標がある。
この距離に基づいた指標を自然勾配という。方策勾配による解法では
自然勾配を用いた方が性能が向上する。
θ
θ
Shun-ichi Amari. Natural Gradient Works Efficiently in Learning, Neural
Computation, Vol. 10, No. 2, pp. 251-276 (1998).
http://www.maths.tcd.ie/~mnl/store/Amari1998a.pdf

11. POMDP（部分観測マルコフ決定過程）
強化学習問題の枠組みでは、マルコフ決定過程を前提にしてきた。
→ 仮に状態系列がマルコフ的だとしても、真の状態を観測できるのか。
Ex. 自分が「不満」なのか「満足」なのか
正しく認識できるのか。
行動 at
環境
報酬 rt
観測 ot
観測
関数状態 st
→ POMDP では、MDP
の枠組みに観測を加
味し、状態は観測と
して知覚されると考
える（一般に、観測
集合も状態集合とは
異なる）。

12. POMDP では状態が手に入らない。状態の確率分布（信念状態）をもつ。
太郎
次郎
次郎
太郎
三郎
信念状態空間 信念状態空間1
1
1
1
1
遠いので真に誰か
わからない
→ いまの観測、
→ 前回の信念状態、
→ 前回の行動
→ からベイズ予測
→ 信念状態を更新 状態集合＝{ 太郎, 次郎 } 状態集合＝{ 太郎, 次郎, 三郎 }
𝑆0~𝑃0 𝑠
𝑆𝑡+1~𝑃 𝑠 𝑆𝑡, 𝐴 𝑡
𝑅𝑡+1~𝑟 𝑆𝑡, 𝐴 𝑡 , 𝑆𝑡+1
𝐴 𝑡~𝜋 𝑎 𝑆𝑡
𝐵0~𝑃0 𝑏
𝐵𝑡+1~𝑃 𝑏 𝐵𝑡, 𝐴 𝑡
𝑅𝑡+1~𝑟 𝐵𝑡, 𝐴 𝑡 , 𝐵𝑡+1
𝐴 𝑡~𝜋 𝑎 𝐵𝑡
？
MDP belief MDP状態 s の代わりに
信念状態 b を用い
れば、POMDP も
MDP と同様の確率
過程となる
（belief MDP）。
s が離散的でも b は
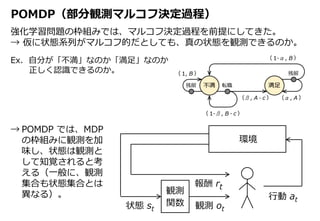
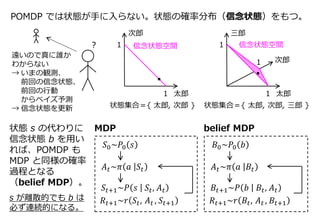
必ず連続的になる。

13. POMDP の場合の最適方策の解法
• belief MDP の Bellman 最適方程式を厳密に解く。
 b が離散的だが限られた場合に解法がある。
• belief MDP の Bellman 最適方程式を近似的に解く（PBVI, PBPI）。
 考える信念状態空間を制限することで計算を計量化したもの。
• その他（価値関数をモデル化しない方法）。
 モンテカルロシミュレーション
‐ POMCP … 信念状態を粒子フィルタで更新する。
 Sarsa による価値反復
 その他の価値反復
 その他