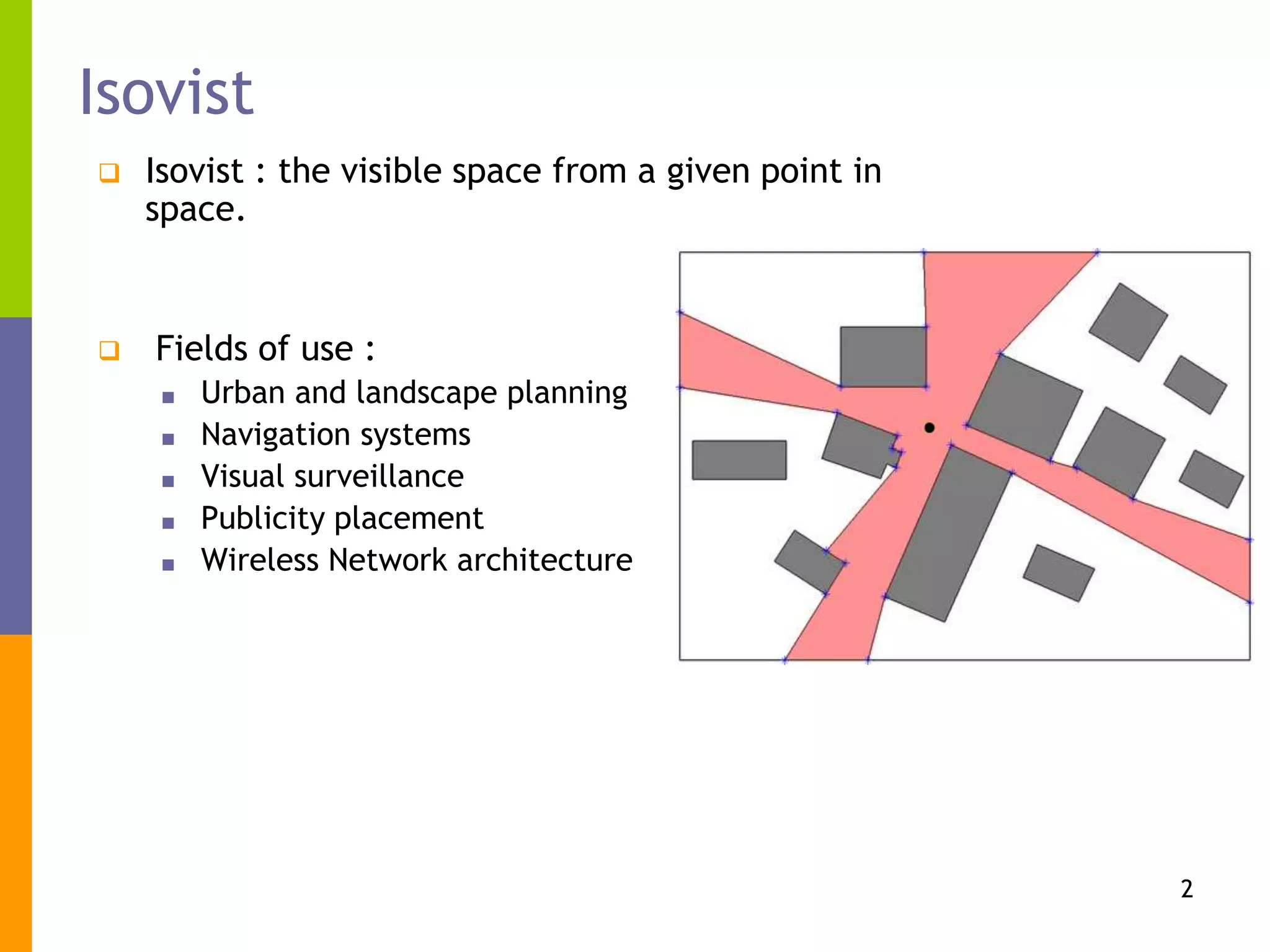
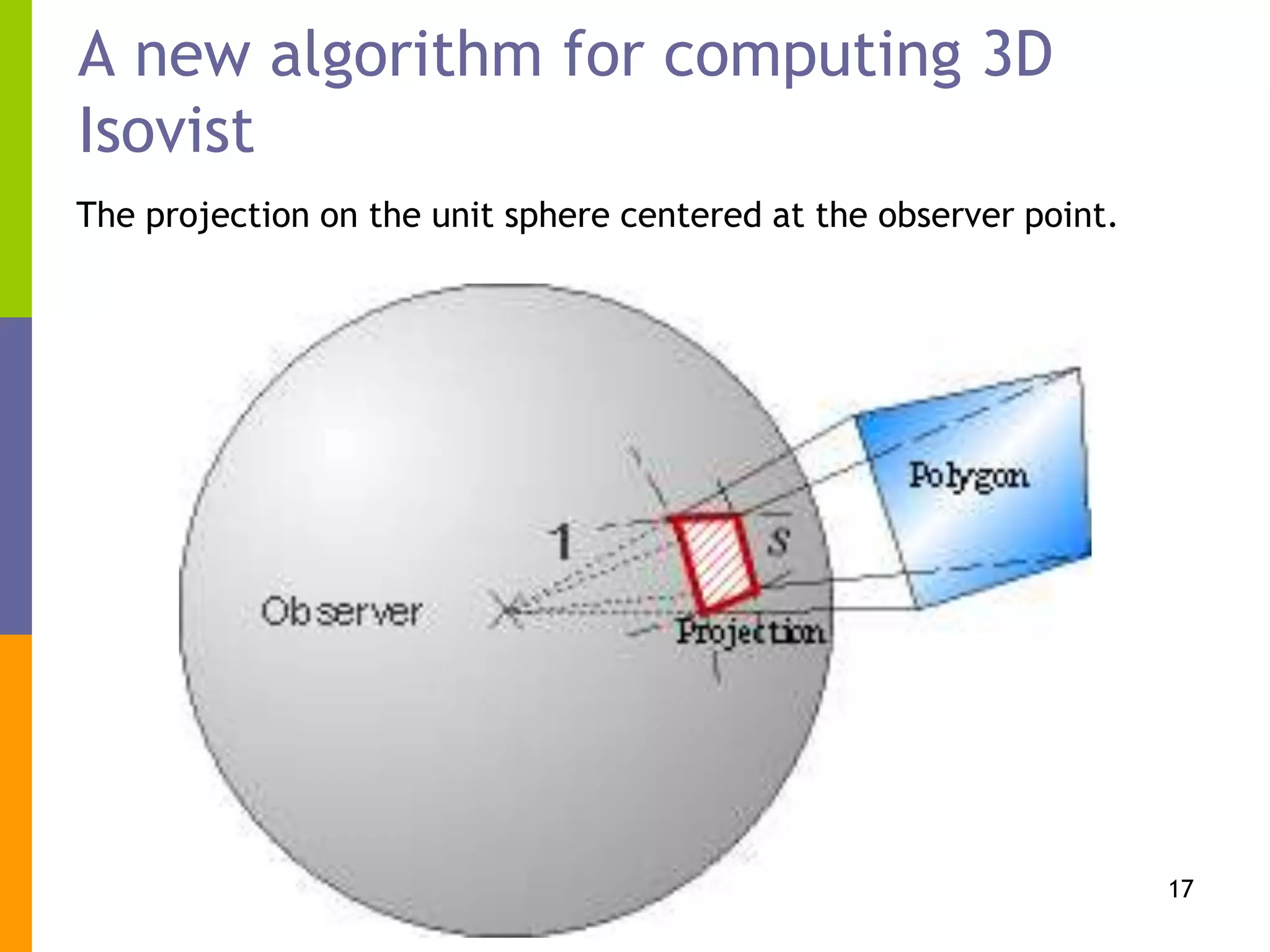
The document presents a new algorithm for computing 2D and 3D isovist, which captures the visible space from a given point, addressing challenges posed by complex topographies and buildings. It details the principles, techniques, and implementations using MATLAB, highlighting applications in urban planning, navigation, and visibility analysis. Future work includes developing standalone software and optimizing calculations through parallel processing.

1. A New Algorithm for 3D Isovist
SULEIMAN Wassim1,
JOLIVEAU Thierry1,
FAVIER Eric2
1ISTHME-ISIG CNRS/UMR EVS, Université Jean Monnet - Saint-Etienne.
2DIPI EA 3719 École Nationale d'Ingénieurs de Saint-Etienne
wassim.suleiman@univ-st-etienne.fr
thierry.joliveau@univ-st-etienne.fr
eric.favier@enise.fr
1
15th International Symposium on Spatial Data Handling (SDH) – August 2012 in Bonn, Germany

2. Isovist
 Isovist : the visible space from a given point in
space.
 Fields of use :
■ Urban and landscape planning
■ Navigation systems
■ Visual surveillance
■ Publicity placement
■ Wireless Network architecture
2

3. Main technique for computing Isovist :
ray tracing
2D Vector data 2.5D Raster data
Brossard & Wieber
Number of rays ? Resolution ?
3

4. 3D ?
Wii home
Challenge:
Dealing with 3D environment composed of buildings laying on
a non-flat topographical surface.
4

5. 2.5 and 3D Isovist solutions
2,5 Raster mode Voxel mode
(Public Eye) (Pyysalo et al. 2009), (Morello & Ratti 2009)
Limitations ?
• The identity and the individuality of the special entities
(buildings for example) is lost
• The precision is related to the resolution
5

6. New algorithms for computing ISOVIST
in 2D and 3D
 The principle is to analyze how the spatial entities
(buildings) block the line-of-sight.
 The isovist will be considered as a group of vision angle
associated with spatial entities or free space (if there
is no building blocking the sight).
6

7. New algorithm for 2D ISOVIST
 Assumption
■ 2D space is an aggregation of segments.
■ We will use the polar coordinates centered at the observer
point.
7

8. New algorithm for 2D ISOVIST

8

9. New algorithm for 2D ISOVIST
 Definition
■ The free segment is a segment whose the two ends are visible
by the observer.
9

10. New algorithm for 2D ISOVIST
 Definition
■ The free vision field is an angle of vision where there is no
obstacle blocking the line of sight.
10

11. New algorithm for 2D ISOVIST

11

12. New algorithm for 2D ISOVIST
Implementation : virtual environment on Matlab
12

13. New algorithm for 2D ISOVIST
Implementation : real GIS data on Matlab
13

14. New algorithm for 2D ISOVIST
Application: dominant type of buildings in view
14

15. 3D data model used for implementing
the 3D Isovist algorithm
 3D environment considered as a constellation of
polygons
■ TIN terrain model +
■ 2D footprints with
height extrusion
3D polygon plane facets (terrain, building)
15

16. A new algorithm for computing 3D
Isovist

16

17. A new algorithm for computing 3D
Isovist
The projection on the unit sphere centered at the observer point.
1
Polygon
Observer
Projection
17

18. A new algorithm for computing 3D
Isovist

18

19. A new algorithm for computing 3D Isovist
 Definitions
■ The free polygon is a polygon whose edges (or the enclosed
frontier segments) are visible from the observer.
19

20. A new algorithm for computing 3D Isovist
 Definitions
■ The free vision field is a solid angle of vision where no obstacle
is blocking the line of sight.
20

21. A new algorithm for computing 3D Isovist

21

22. A new algorithm for computing 3D Isovist
Implementation on Matlab
22

23. A new algorithm for computing 3D Isovist
Verification and validation: the comparison between our 3d isovist and the real
visibility
The image by The image in
the 3D isovist The real world
2D/3D registration
(Edges and corners matching)
23

24. A new algorithm for computing 3D Isovist
Application: Computing visibility indices
Open sky index with IDW interpolation Visibility of target building with IDW interpolation
Visibility of target
building with solid
angle of vision
interpolation
24

25. Conclusion
 We propose a new algorithm for computing Isovist in
2D and 3D environment with non-flat topographical
surface
 It permits the calculation of classic visibility indices
and new ones like the content of the view (e.g. the
percentage of historic building in a view)
25

26. Future work
 Developing a stand alone program to achieve the
calculation.
 Using parallel processing like using cuda over GPU.
 Implementation in the hardware or in a low level
programming language.
 Thinking about meaning and definition of 3D Visibility
indices (vertical and horizontal surfaces).
26

27. Thank you
for your attention !
27