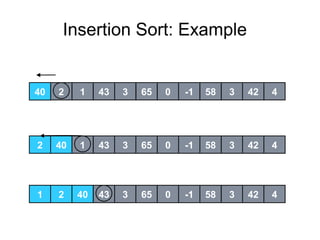
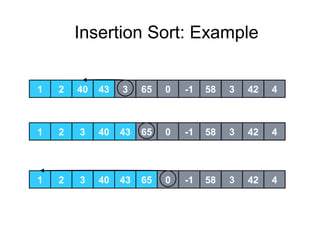
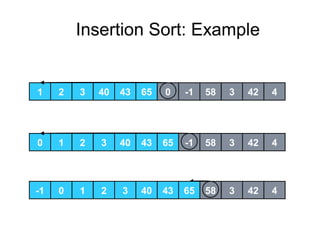
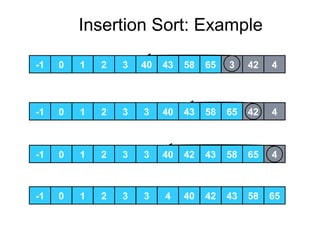
Insertion sort is a sorting algorithm that works by building a sorted array (or list) one item at a time. It maintains two groups, a sorted group and an unsorted group. It removes one element from the unsorted group, finds the location it belongs within the sorted group, and inserts it there. This continues until the unsorted group is empty, leaving a fully sorted list. The worst-case running time is O(n^2) as each insertion may require traversing the entire sorted portion. However, the average case is O(n) for nearly sorted data. A lower bound analysis shows that any algorithm relying on adjacent swaps has a worst case lower bound of Ω(n^2).

1. Insertion Sort

2. Insertion Sort: Idea

Idea: sorting cards.
− 8 | 5 9 2 6 3
− 5 8 | 9 2 6 3
− 5 8 9 | 2 6 3
− 2 5 8 9 | 6 3
− 2 5 6 8 9 | 3
− 2 3 5 6 8 9 |

3. Insertion Sort: Idea
1. We have two group of items:
 sorted group, and
 unsorted group
1. Initially, all items in the unsorted group
and the sorted group is empty.
 We assume that items in the unsorted
group unsorted.
 We have to keep items in the sorted group
sorted.
1. Pick any item from, then insert the item
at the right position in the sorted group to

4. 40 2 1 43 3 65 0 -1 58 3 42 4
2 40 1 43 3 65 0 -1 58 3 42 4
1 2 40 43 3 65 0 -1 58 3 42 4
40
Insertion Sort: Example

5. 1 2 3 40 43 65 0 -1 58 3 42 4
1 2 40 43 3 65 0 -1 58 3 42 4
1 2 3 40 43 65 0 -1 58 3 42 4
Insertion Sort: Example

6. 1 2 3 40 43 65 0 -1 58 3 42 4
1 2 3 40 43 650 -1 58 3 42 4
1 2 3 40 43 650 58 3 42 41 2 3 40 43 650-1
Insertion Sort: Example

7. 1 2 3 40 43 650 58 3 42 41 2 3 40 43 650-1
1 2 3 40 43 650 58 42 41 2 3 3 43 650-1 5840 43 65
1 2 3 40 43 650 42 41 2 3 3 43 650-1 5840 43 65
Insertion Sort: Example
1 2 3 40 43 650 421 2 3 3 43 650-1 584 43 6542 5840 43 65

8. Insertion Sort: Analysis

Running time analysis:
− Worst case: O(N2
)
− Best case: O(N)

9. A Lower Bound

Bubble Sort, Selection Sort, Insertion
Sort all have worst case of O(N2
).

Turns out, for any algorithm that
exchanges adjacent items, this is the
best worst case: Ω(N2
)

In other words, this is a lower bound!

10. How many squares can you create in this figure by connecting any 4
dots (the corners of a square must lie upon a grid dot?
TRIANGLES:
How many triangles are located in the image below?

11. There are 11 squares total; 5 small, 4 medium, and 2 large.
27 triangles. There are 16 one-cell triangles, 7 four-cell triangles, 3 nine-cell triangles, and
1 sixteen-cell triangle.

12. GUIDED READING