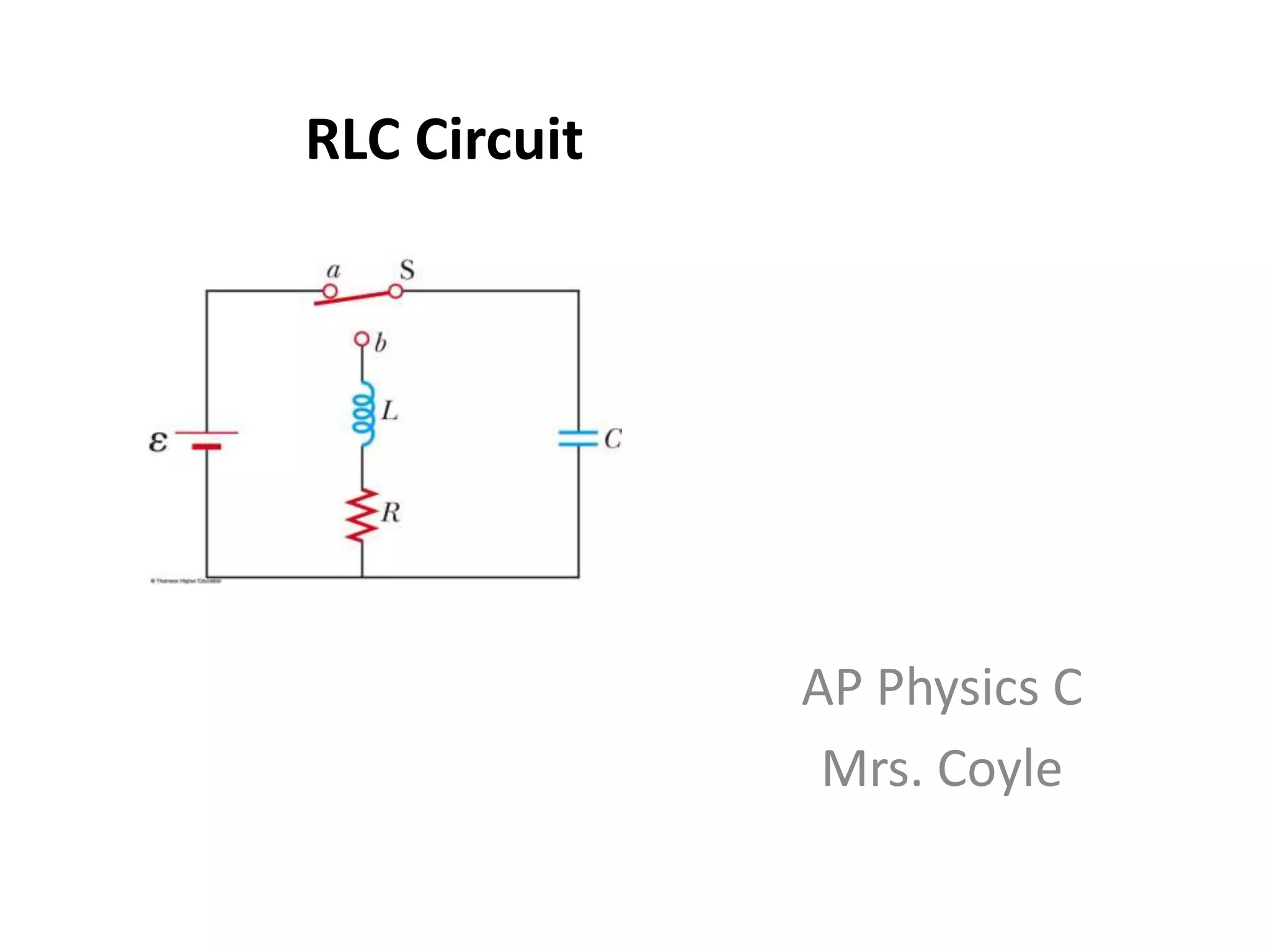
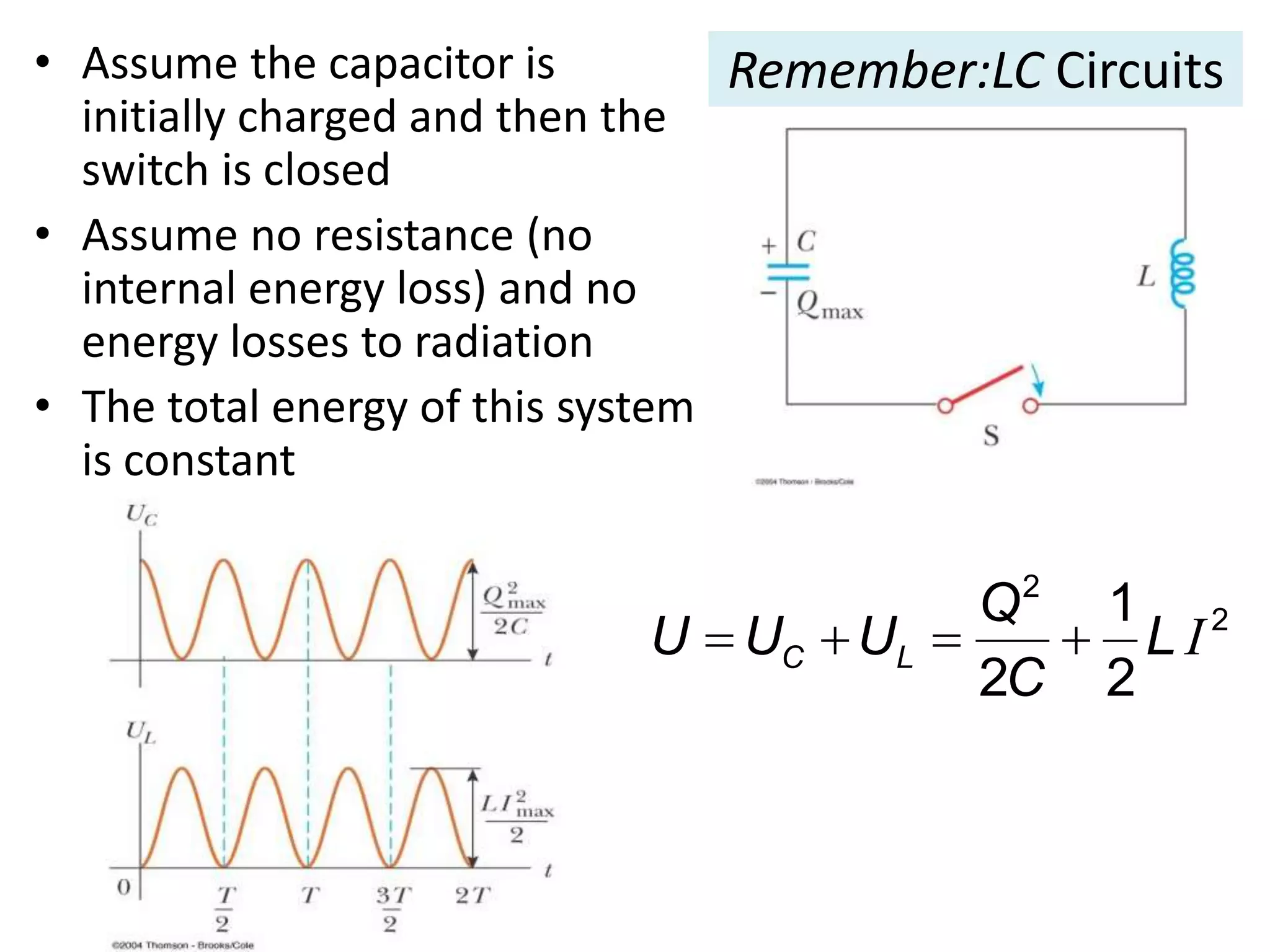
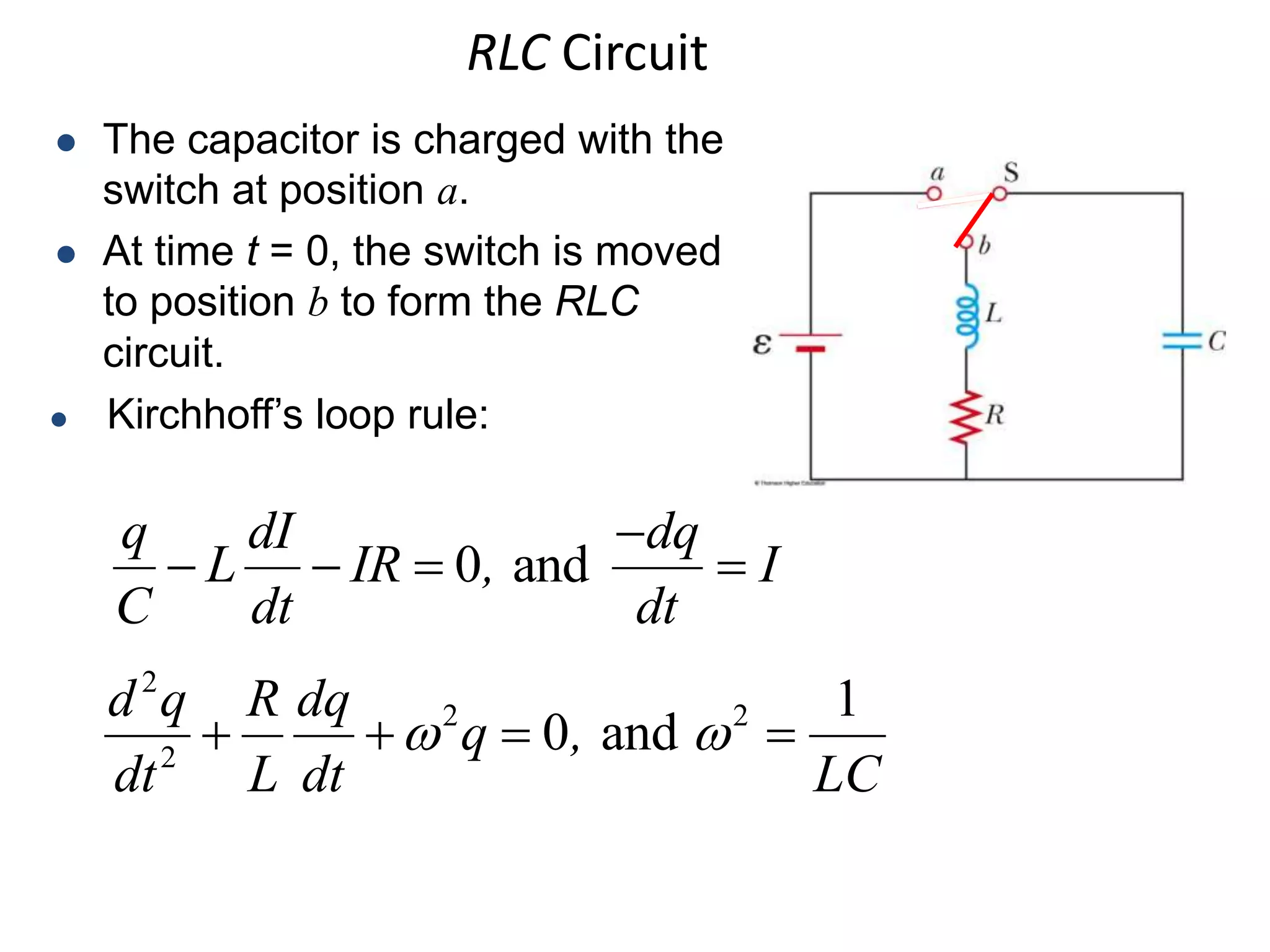
An RLC circuit consists of a resistor, inductor, and capacitor connected in a loop. When the switch is closed, current flows through the circuit. Some energy is lost to heat in the resistor over time, causing the total energy of the circuit to decrease similarly to a damped mass-spring system. The current and charge oscillate at the circuit's resonant frequency. Kirchhoff's laws can be applied to derive equations describing the oscillating current and charge in the RLC circuit.

1. RLC Circuit
AP Physics C
Mrs. Coyle

2. RLC circuit
• In real circuits, there is some resistance, and some
energy is lost to internal energy for the resistor
(heat).
• (Some energy is also lost to radiation but this is
ignored).
• Therefore the total energy of the circuit decreases
over time similar to damping in a mass-spring
system.

3. Remember:LC Circuits• Assume the capacitor is
initially charged and then the
switch is closed
• Assume no resistance (no
internal energy loss) and no
energy losses to radiation
• The total energy of this system
is constant
2
21
2 2
IC L
Q
U U U L
C
   

4. Simulation
http://phet.colorado.edu/en/simulation/circu
it-construction-kit-ac

5. RLC Circuit
 The capacitor is charged with the
switch at position a.
 At time t = 0, the switch is moved
to position b to form the RLC
circuit.
 Kirchhoff’s loop rule:
0 and
q dI dq
L IR , I
C dt dt

   
2
2 2
2
1
0 and
d q R dq
q ,
dt L dt LC
    

6. RLC Circuit
  22
1
with
2
R
t
L
max d d
R
q Q e cos t ,
LC L
 

  
   2
2
R
t
L
max d d d
R
I Q e sin t cos t
L
  
  
  
 