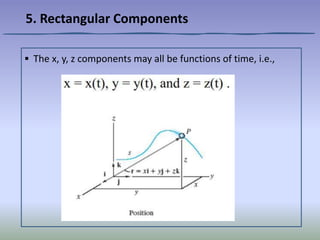
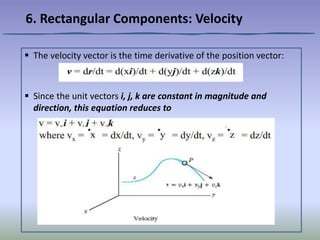
This document discusses describing particle motion using rectangular components relative to a fixed frame of reference. It defines the position vector and velocity vector as the time derivative of position. The acceleration vector is defined as the time derivative of velocity. An example problem is given to find the point of collision and speeds of two particles before collision by setting their position vectors equal and differentiating to find velocities.

1.  It is often convenient to describe the motion of a particle in terms
of its x, y, z or rectangular components, relative to a fixed frame
of reference.
 The position of the particle can be defined at any instant by the
position vector,
5. Rectangular Components

2.  The x, y, z components may all be functions of time, i.e.,
5. Rectangular Components

3.  The velocity vector is the time derivative of the position vector:
 Since the unit vectors i, j, k are constant in magnitude and
direction, this equation reduces to
6. Rectangular Components: Velocity

4.  The acceleration vector is the time derivative of the velocity vector:
The magnitude of the acceleration vector is:
7. Rectangular Components: Acceleration

5. CURVILINEAR MOTION
Example
Given:
The motion of two particles (A and B) is described by the position vectors.
Find:
The point at which the particles collide and their speeds just before the
collision.
Plan:
1) The particles will collide when their position vectors are equal,
or rA= r B
2) Their speeds can be determined by differentiating the position
vectors.

6. CURVILINEAR MOTION
Solution

7. CURVILINEAR MOTION
Solution