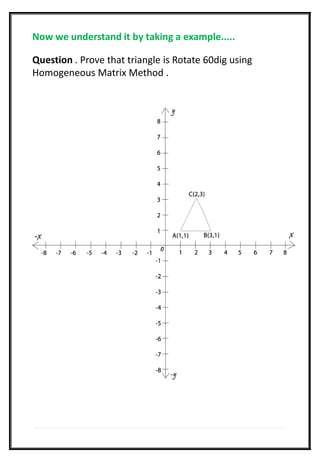
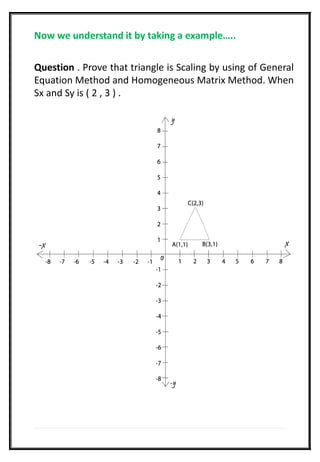
This document is a project report submitted by Vishal Loungani towards the partial fulfillment of a bachelor's degree in computer application. The report discusses various 2D transformations in computer graphics including translation, rotation, and scaling. It provides examples of applying each transformation using both the classic method and homogeneous matrix method. For translation, rotation by 60 degrees, and scaling by factors of 2 and 3 are shown. The transformations are applied to the coordinates of a sample triangle and the results are presented.

1. Computer Graphics
Assessment
Presented By
Vishal Loungani
Bachelors of Computer Application – Second Year
Dezyne E’cole College, Ajmer

2. Project report on
Computer Graphics Assessment
Submitted To
Dezyne E’cole College
Towards
The Partial Fulfilment
Of 2019 Year, Bachelor of Computer Application
By
Vishal Loungani
Dezyne E’cole College
106/10, Civil Line, Ajmer
www.dezyneecole.com

3. Acknowledgment
I Am Vishal Loungani Student of Bachelor Of Computer Application,
Dezyne E’cole College. I Would Like To Express My Gratitude to Each
And Every Person Who Has Contributed in Encouraging Me And
Helping Me to Coordinate My Project.
I Also Thank Dezyne E’cole College Who Provided Insight And Expertise
That Greatly Assisted the Project. A Special Thanks To My Teachers,
Parents and Colleagues Who Have Supported Me at Every Step. Not
To Forget, the Almighty Who Blessed Me With Good Health Because
of Which I Worked More Efficiently And Better.

4. 2-D Viewing
2-D Transformation ?
Changes in the Orientation ,size , shape or position
of an object, such that the coordinates values of
the object changes, is known as transformation.
The three Basic transformations are :
1. Translation.
2. Rotation.
3. Scaling.
From this basic transformation .
The two more transformation derived it is known
as Derived transformation.
1. Shearing.
2. Reflection.

5. 1) Classic Method: In Computer Graphics we use classic
translation method in Graphs .
For classic translation First we have tx and ty given in
Question . After this we have calculate Q by using classic
Method .
1. Translation: Whenever we change the position
of an object such that the coordinates values change
then it is called translation .
Under it we follow two types of methods shown below.
1) Classic Method .
2) Homogeneous Matrix Method .
I. Q’=Q + T
Where
Q’= New Coordinates.
T=Translation Distance.
Q= Original Coordinates.
II. x’=x + tx
y’=y+ ty
2) Homogeneous Matrix Method are shown in Example .

6. Now we take Example….
Question . Prove that triangle Translation by using of Classic
Method and Homogeneous Matrix Method. When tx and ty is
( 2 , 3 ) .

7. Solution :
By use classic Method :
tx =2
ty =3
Q is = A(1,1) B(3,1) C(2,3)
Q’ = New Coordinates
A x’ = x + tx
1 + 2 = 3
y’ = y + ty
1 + 3 = 4
B x’ = x + tx
3 + 2 = 5
y’ = y + ty
1 + 3 = 4
C x’ = x + tx
2 + 2 = 4
y’ = y + ty
3 + 3 = 6
Q’ is = A(3,4) B(5,4) C(4,6)

8. By use of Homogeneous Matrix Method :
1 0 tx
0 1 ty
0 0 1
1 3 2
1 1 3
1 1 1
A B C
x
y
*
1 0 2
0 1 3
0 0 1
1 3 2
1 1 3
1 1 1
A B C
x
y
*
1+0+2 3+0+2 2+0+2
0+1+3 0+1+3 0+3+3
0+0+1 0+0+1 0+0+1
3 5 4
4 4 6
1 1 1
A B C
x
y Ans. Q’ is = A(3,4) B(5,4) C(4,6)
A B C
x
y

9. Ans.

10. 2. Rotation: In order to rotate an object we need to rotate
each vertex of the figure individually. On rotating a point
P(x, y) by an angle A about the origin we get a point P'(x’, y’).
The values of x’ and y’ can be calculated as follows:-
We know that,
x = rcosB, y = rsinB
x’ = rcos(A+B) = r( cosAcosB – sinAsinB) =
rcosBcosA – rsinBsinA = xcosA – ysinA
y’ = rsin(A+B) = r( sinAcosB + cosAsinB) =
rcosBsinA + rsinBcosA = xsinA + ycosA
Types of Rotation:
1. Anticlockwise: The positive value of the pivot point
(rotation angle) rotates an object in a counter-clockwise
(anti-clockwise) direction.
2. Counterclockwise: The negative value of the pivot point
(rotation angle) rotates an object in a clockwise direction.

11. 1. Matrix for rotation is a clockwise direction.
Matrix for homogeneous co-ordinate rotation (anticlockwise)
Matrix for homogeneous co-ordinate rotation (clockwise)
2. Matrix for rotation is an anticlockwise direction.
Rotation by Matrix in two Types :

12. Now we need a Trigonometry Table for find a value of
cos Θ and sin Θ in different degrees of angels :
Trigonometry Table
Θ 0° 30° 45° 60° 90°
sinΘ 0 0.5 0.7 0.87 1
cosΘ 1 0.87 0.7 0.5 0

13. Question . Prove that triangle is Rotate 60dig using
Homogeneous Matrix Method .
Now we understand it by taking a example.....

14. Solution:
Using by Homogeneous Matrix: Rotate 60° :
Cos Θ -Sin Θ 0
Sin Θ Cos Θ 0
0 0 1
1 3 2
1 1 3
1 1 1
A B C
x
y
*
0.50 -0.87 0
0.87 0.50 0
0 0 1
1 3 2
1 1 3
1 1 1
A B C
x
y
*
0.50+(-0.87)+0 1.50+(-0.87)+0 1+(-2.61)+0
0.87+0.50+0 2.61+0.50+0 1.74+1.50+0
0+0+1 0+0+1 0+0+1
-0.37 0.63 -1.61
1.37 3.11 3.2
1 1 1
A’ B’ C’
x
y
A’ B’ C’
x
y
Now we Round figure
it for make accuracy in
new coordinates .

15. 0 1 -2
1 3 3
1 1 1
A’ B’ C’
x
y
Our new round figure coordinates is.
Ans. New Coordinates of object on 60dig rotation is .
X , Y
A=(0,1)
B=(1,3)
C=(-2,3)

16. Ans.

17. 3. Scaling: To change the size of an object, scaling
transformation is used. In the scaling process ,
you either expand or compress the dimensions
of the object. Scaling can be achieved by multipl-
-ying the original coordinates of the object with
the scaling factor to get the desired result.
Let us assume that the original coordinates are (X,Y)
, the scaling factors are (SX, SY), and the produced
coordinates are (X’, Y’). This can be mathematically
represented as shown below −
X' = X . SX and Y' = Y . SY
The scaling factor sx, sy scales the object in X and Y
direction respectively. So, the below equation can be
represented in matrix form:

18. For homogeneous coordinates, the below scaling matrix may
be represented like a 3 x 3 matrix as-

19. Now we understand it by taking a example…..
Question . Prove that triangle is Scaling by using of General
Equation Method and Homogeneous Matrix Method. When
Sx and Sy is ( 2 , 3 ) .

20. Solution :
By use General Equation Method :
Sx =2
Sy =3
Q is = A(1,1) B(3,1) C(2,3)
Q’ is for = New Coordinates
A x’ = x . sx
1 * 2 = 2
y’ = y . sy
1 * 3 = 3
B x’ = x . sx
3 * 2 = 6
y’ = y . sy
1 * 3 = 3
C x’ = x . sx
2 * 2 = 4
y’ = y . sy
3 * 3 = 9
Q’ is = A(2,3) B(6,3) C(4,9)

21. By use of Homogeneous Matrix Method :
sx 0 0
0 sy 0
0 0 1
1 3 2
1 1 3
1 1 1
A B C
x
y
*
2 0 0
0 3 0
0 0 1
1 3 2
1 1 3
1 1 1
A B C
x
y
*
2+0+0 6+0+0 4+0+0
0+3+0 0+3+0 0+9+0
0+0+1 0+0+1 0+0+1
2 6 4
3 3 9
1 1 1
A B C
x
y Ans. Q’ is = A(2,3) B(6,3) C(4,9)
A B C
x
y

22. Ans.

23. Thank You
Presented By
Vishal Loungani
Bachelors of Computer Application
Dezyne E’cole College
www.dezyneecole.com