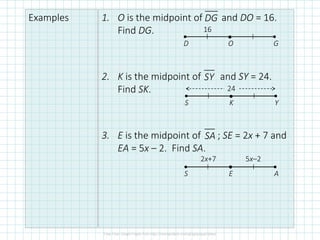
The document outlines the segment addition postulate, including how to calculate distances between points on a number line and graph and solving linear equations using midpoint properties. It introduces key terms like congruent segments, bisecting, and midpoints with examples demonstrating their application. The importance of using proper notation is emphasized, highlighting that distance is always a positive value.

1. Segment Addition Postulate
Objectives:
• Calculate the distance between two points on a number
line and on a graph
• Set up and solve linear equations using midpoint
properties
• Correctly use notation for distance and segments

2. distancedistancedistancedistance – the absolute value of the difference of the
coordinates. Also called the lengthlengthlengthlength.
Example:
The distance from R to S is written RS:
Distance is alwaysalwaysalwaysalways positive. If you come up with a
negative answer, you’ve done something wrong!
Notation: Notice the different notations:
AB line AB
segment AB
AB length AB
AB
2 3 5 5RS = − − = − =
R S

3. congruent segmentscongruent segmentscongruent segmentscongruent segments – segments that have the same length.
Notation: “Tick marks” indicate congruent segments. To
match more than one set of congruent segments, match
up the tick marks (2 tick marks go with 2 tick marks, etc.)
YX
A B
Since XY , (and vice versa)AB XY AB= ≅
• •
t

4. betweenbetweenbetweenbetween – point B is between two points A and C if all three
points are collinearcollinearcollinearcollinear and
AB + BC = AC.
(part + part = whole)
Note: This is also called the Segment Addition PostulateSegment Addition PostulateSegment Addition PostulateSegment Addition Postulate.
●
A B C

5. bisectbisectbisectbisect – to cut or divide into two congruent pieces.
Example:
Point B bisectsbisectsbisectsbisects FI ⇒ FB = BI
midpointmidpointmidpointmidpoint – the point that bisects a segment.
Example: Point B is the midpointmidpointmidpointmidpoint of FI.
●
F B I

6. Examples 1. O is the midpoint of and DO = 16.
Find DG.
2. K is the midpoint of and SY = 24.
Find SK.
3. E is the midpoint of ; SE = 2x + 7 and
EA = 5x – 2. Find SA.
DG
SY
SA
●
D O G
16
●
S K Y
24
●
S E A
2x+7 5x–2

7. Examples 1. O is the midpoint of and DO = 16.
Find DG.
2. K is the midpoint of and SY = 24.
Find SK.
3. E is the midpoint of ; SE = 2x + 7 and
EA = 5x – 2. Find SA.
DG
SY
SA
●
D O G
16
●
S K Y
24
●
S E A
2x+7 5x–2
DO + OG = DG
16 + 16 = 32
SK = ½ SY = ½(24) = 12
SE = EA
2x + 7 = 5x – 2
9 = 3x
x = 3
SA = SE + EA
= 2(3)+7+5(3)-2
= 26