2013 osnk fisika (tkunci)

OSN Fisika Bedah soal
2013(kab/kota)
180 http://ibnu2003.blogspot.com
1. Pembahasan
a. besar kecepatan benda ( 𝑣⃗( 𝑡)) saat t=2 detik dan t=4 detik
kecepatan benda [ 𝑣⃗( 𝑡)] dalam bidang xy dapat dituliskan
dengan vektor satuan [ 𝑖] pada arah sumbu x dan [ 𝑗] pada
arah sumbu y, maka persamaan [ 𝑣⃗( 𝑡)] adalah :
𝑣⃗( 𝑡) = 𝑣𝑥( 𝑡) 𝑖 + 𝑣𝑦( 𝑡) 𝑗
pada saat t=2 detik
𝑣𝑥( 𝑡) = (3𝑡2
− 4𝑡 + 5) 𝑚/𝑑𝑡
𝑣𝑥(2) = (3.22
− 4.2 + 5) = 9𝑚/𝑑𝑡
𝑣𝑦(2) = 30𝑚/𝑑𝑡(𝑙𝑖ℎ𝑎𝑡 𝑔𝑎𝑚𝑏𝑎𝑟)
sehingga :
𝑣⃗(2) = 𝑣𝑥(2) 𝑖 + 𝑣𝑦(2) 𝑗
𝑣⃗(2) = (9𝑖 + 30𝑗) 𝑚/𝑑𝑡
pada saat t=4 detik
𝑣𝑥( 𝑡) = (3𝑡2
− 4𝑡 + 5) 𝑚/𝑑𝑡
𝑣𝑥(4) = (3.42
− 4.4 + 5) = 37𝑚/𝑑𝑡
pada selah waktu (3 ≤ 𝑡 ≤ 5) detik dalan arah sumbu y
benda bergerak dengan percepatan konstan, maka
percepatan pada sumbu y :
−10
−20
−30
−40
10
20
30
40
50
60
10 11 121 2 3 4 5 6 7 8 9
𝑣(𝑡)(𝑚/𝑠)
𝑡(𝑑𝑡)

2013(kab/kota)
𝑎 𝑦 =
𝑣𝑦(5) − 𝑣𝑦(3)
∆𝑡
=
60 − 30
5 − 3
= 15𝑚/𝑑𝑡2
maka percepatan benda selang waktu (3 ≤ 𝑡 ≤ 4) detik sama
dengan selang waktu (3 ≤ 𝑡 ≤ 5) detik
sehingga kecepatan pada sumbu y pada 4 detik
𝑣𝑦( 𝑡) = 𝑣𝑦(3) + 𝑎 𝑦∆𝑡
𝑣𝑦(4) = 30+ 15.(4 − 3) = 45𝑚/𝑑𝑡
maka persamaan vektor kecepatan pada 4 detik adalah :
𝑣⃗(4) = 𝑣𝑥(4) 𝑖 + 𝑣𝑦(4) 𝑗
𝑣⃗(4) = (37𝑖 + 45𝑗) 𝑚/𝑑𝑡
b. besar Percepatan benda ( 𝑎⃗( 𝑡)) saat t=4 detik
turunkan fungsi kecepatan terhadap waktu, maka
memperoleh persamaan percepatan.
𝑎 𝑥( 𝑡) =
𝑑𝑣𝑥( 𝑡)
𝑑𝑡
=
𝑑
𝑑𝑡
(3𝑡2
− 4𝑡 + 5)
𝑎 𝑥( 𝑡) = (6𝑡 − 4) 𝑚/𝑑𝑡2
sehingga :
𝑎 𝑥(4) = (6.4 − 4) = 20𝑚/𝑑𝑡2
percepatan arah sumbu y :
𝑎 𝑦(4) = 15𝑚/𝑑𝑡2
maka persamaan vektor percepatan menjadi
𝑎(4) = 𝑎 𝑥(4) 𝑖 + 𝑎 𝑦(4) 𝑗
𝑎(4) = (20𝑖 + 15𝑗)𝑚/𝑑𝑡2
c. besar posisi benda ( 𝑟⃗( 𝑡)) saat t=9 detik, jika posisi awal
benda adalah [ 𝑟⃗(0) = (74𝑖 + 40𝑗) 𝑚]
persaman vektor posisi benda pada sumbu xy adalah :
𝑟⃗( 𝑡) = 𝑟𝑥( 𝑡) 𝑖 + 𝑟𝑦( 𝑡) 𝑗
pada waktu t=0, maka
𝑟⃗(0) = 𝑟𝑥(0) 𝑖 + 𝑟𝑦(0) 𝑗 = (74𝑖 + 40𝑗) 𝑚
poisisi benda pada t=9 detik diperoleh dari :
mengintegralkan fungsi kecepatan terhadap waktu
𝑣𝑥( 𝑡) =
𝑑𝑥( 𝑡)
𝑑𝑡
⇋ 𝑣𝑥( 𝑡) 𝑑𝑡 = 𝑑𝑥( 𝑡)
𝑥( 𝑡) = ∫ 𝑣𝑥( 𝑡) 𝑑𝑡
𝑥( 𝑡) = ∫ (3𝑡2
− 4𝑡 + 5) 𝑑𝑡
𝑥( 𝑡) = 𝑡3
− 2𝑡2
+ 5𝑡 + 𝐶
pada saat t=0, nilai C adalah :[ 𝑟𝑥(0) = 74]

2013(kab/kota)
persamaan posisinya menjadi
𝑥( 𝑡) = ( 𝑡3
− 2𝑡2
+ 5𝑡 + 74) 𝑚
sehingga pada t=9 detik, posisi benda terhadap sumbu x
adalah :
𝑥(9) = (93
− 2. 92
+ 5.9+ 74) 𝑚 = 686𝑚
meninjau gerak benda pada sumbu y, maka luas grafik [ 𝑦( 𝑡)]
terhadap waktu menunjukkan nilai dari [ 𝑦( 𝑡)].
maka nilai [ 𝑦(9)] merupakan jumlah aljabar luas grafik :
luas I (0 ≤ 𝑡 ≤ 3) = 3.30 = 90𝑚
luas II (3 ≤ 𝑡 ≤ 5) = 0,5(5 − 3)(30+ 60) = 90𝑚
luas III (5 ≤ 𝑡 ≤ 8) = 0,5.3.60 = 90𝑚
luas IV (5 ≤ 𝑡 ≤ 8) = 0,5.1.(−20) = −10𝑚
total [ 𝑦(9) = 𝐼 + 𝐼𝐼 + 𝐼𝐼𝐼 + 𝐼𝑉 + 𝑦(0)]
𝑦(9) = 90 + 90+ 90− 10 + 40 = 300𝑚
sehingga posisi vektor pada t=9 detik adalah :
𝑟⃗(9) = 𝑟𝑥(9) 𝑖 + 𝑟𝑦(9) 𝑗
𝑟⃗(9) = 686𝑖 + 300𝑗
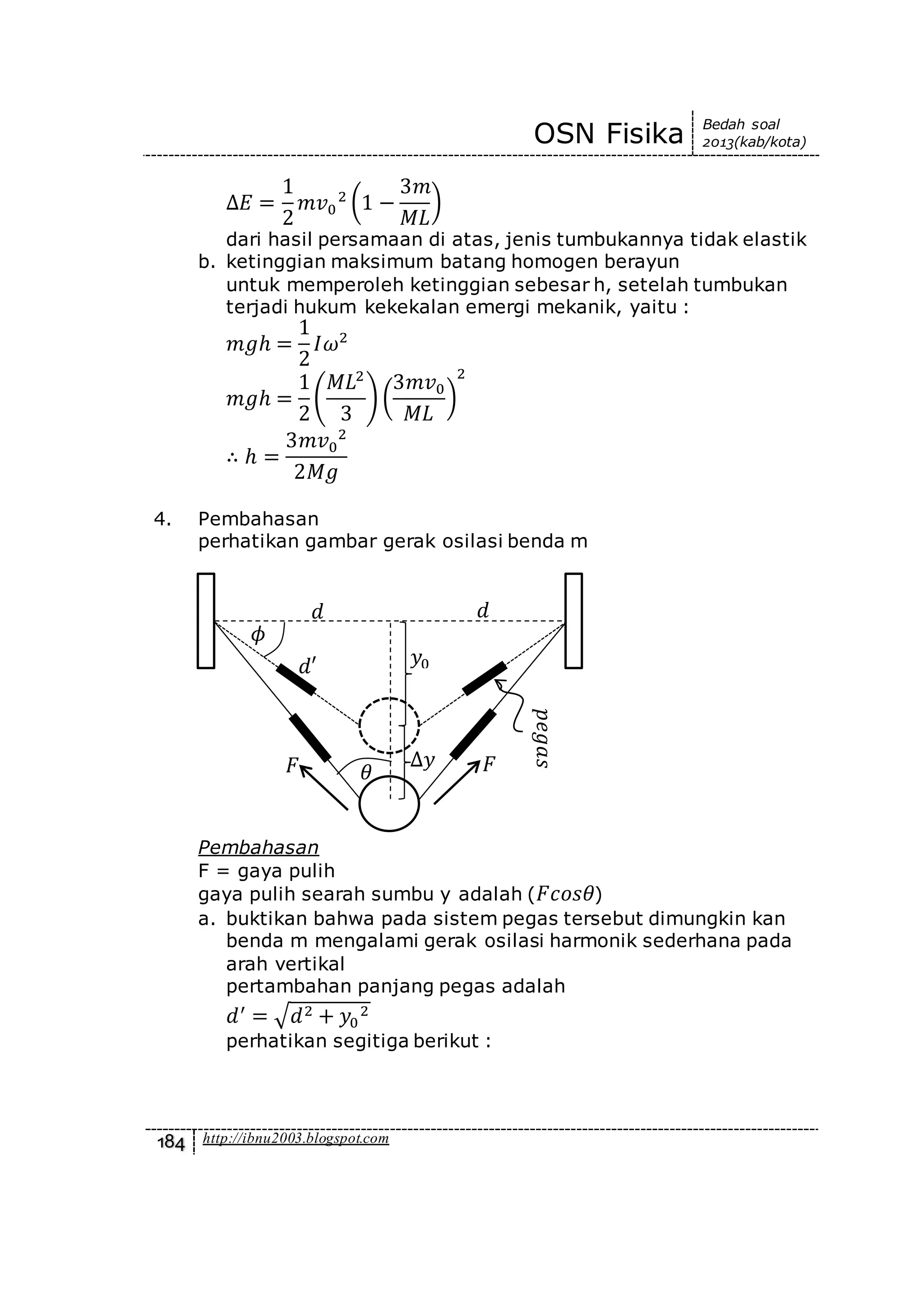
2. Pembahasan
perhatikan gambar diagram bebas sistem di bawah ini
Seseorang massa 60kg tersebut akan diam pada posisi tertentu
saat orang tersebut mempertahankan dirinya untuk tidak
menyentuk lantai. gaya yang harus diberikan orang tersebut ke
tali agar orang ini bisa mempertahamkan diri agar tidak
menyentuh lantai adalah gaya tegangan T1.
𝑇1 + 𝑇2 = 𝑚𝑔 ⇋ 𝑇2 = 2𝑇1
𝑚𝑔
𝑇1 𝑇1
𝑇1
𝑇2

2013(kab/kota)
maka :
3𝑇1 = 𝑚𝑔 ⇋ 𝑇1 =
𝑚𝑔
3
=
600
3
= 200𝑁
3. Pembahasan
berikut gerakan benda setelah tumbukan
a. kasus diatas termasuk tumbukan elastik atau tak elastik
Setalah tumbukan benda m diam dan batang memiliki
kecepatan sudut ( 𝜔). hukum kekekalan momentum sudut
sebelum dan sesudah tumbukan dengan mengambil acuan
langit-langit, sehingga :
𝐿 𝑠𝑒𝑏𝑒𝑙𝑢𝑚 = 𝐿 𝑠𝑒𝑠𝑢𝑑𝑎ℎ
𝑚𝑣0 𝐿 = 𝐼𝜔
momen inersia batang yang berotasi pada ujungnya adalah :
𝐼 =
𝑀𝐿2
3
maka :
𝑚𝑣0 𝐿 =
𝑀𝐿2
3
𝜔
𝜔 =
3𝑚𝑣0
𝑀𝐿
energi yang hilang karena proses tumbukan adalah :
∆𝐸 = 𝐸𝑘( 𝑎𝑤𝑎𝑙) − 𝐸𝑘( 𝑎𝑘ℎ𝑖𝑟)
∆𝐸 =
1
2
𝑚𝑣0
2
−
1
2
𝐼𝜔2
∆𝐸 =
1
2
𝑚𝑣0
2
−
1
2
(
𝑀𝐿2
3
)(
3𝑚𝑣0
𝑀𝐿
)
2
𝑑𝑖𝑎𝑚
ℎ
𝜔𝑚

2013(kab/kota)
∆𝐸 =
1
2
𝑚𝑣0
2
(1 −
3𝑚
𝑀𝐿
)
dari hasil persamaan di atas, jenis tumbukannya tidak elastik
b. ketinggian maksimum batang homogen berayun
untuk memperoleh ketinggian sebesar h, setelah tumbukan
terjadi hukum kekekalan emergi mekanik, yaitu :
𝑚𝑔ℎ =
1
2
𝐼𝜔2
𝑚𝑔ℎ =
1
2
(
𝑀𝐿2
3
) (
3𝑚𝑣0
𝑀𝐿
)
2
∴ ℎ =
3𝑚𝑣0
2
2𝑀𝑔
4. Pembahasan
perhatikan gambar gerak osilasi benda m
Pembahasan
F = gaya pulih
gaya pulih searah sumbu y adalah ( 𝐹𝑐𝑜𝑠𝜃)
a. buktikan bahwa pada sistem pegas tersebut dimungkin kan
benda m mengalami gerak osilasi harmonik sederhana pada
arah vertikal
pertambahan panjang pegas adalah
𝑑′
= √𝑑2 + 𝑦0
2
perhatikan segitiga berikut :
𝑑𝑑
𝐹𝐹
𝑦0𝑑′
∆𝑦
𝜙
𝜃
𝑝𝑒𝑔𝑎𝑠

2013(kab/kota)
data-data yang diperlukan
𝑐𝑜𝑠𝜃 =
𝑦0 + ∆𝑦
√ 𝑑2 + (𝑦0 + ∆𝑦)2
⇋ 𝑐𝑜𝑠𝜙 =
𝑦0
√ 𝑑2 + 𝑦0
2
𝑥 = (𝑑2
+ 𝑦0
2
) + 2𝑦0∆𝑦 + ∆𝑦2
𝑥 = 𝑑′2
+ 2𝑦0∆𝑦 + ∆𝑦2
pertambahan panjang pegas searah sumbu y adalah
∆𝑦 = 𝑥 − 𝑑′
∆𝑦 = √𝑑2 + (𝑦0 + ∆𝑦)2 − 𝑑′
gaya pulih pada benda m
𝐹𝑝𝑢𝑙𝑖ℎ = −2𝐹𝑐𝑜𝑠𝜃
= −2𝑘(√𝑑2 + (𝑦0 + ∆𝑦)2 − 𝑑′)(
𝑦0 + ∆𝑦
√ 𝑑2 + (𝑦0 + ∆𝑦)2
)
= −2𝑘(𝑦0 + ∆𝑦 −
𝑑′[𝑦0 + ∆𝑦]
√ 𝑑2 + (𝑦0 + ∆𝑦)2
)
= −2𝑘(𝑦0 + ∆𝑦 −
𝑑′[𝑦0 + ∆𝑦]
√ 𝑑2 + (𝑦0 + ∆𝑦)2
)
= −2𝑘(𝑦0 + ∆𝑦)(1 −
𝑑′
√ 𝑑2 + (𝑦0 + ∆𝑦)2
)
= −2𝑘𝑦0(1 +
∆𝑦
𝑦0
)(
√ 𝑑′2 + 2𝑦0∆𝑦 + ∆𝑦2 − √ 𝑑′2
√ 𝑑′2 + 2𝑦0∆𝑦 + ∆𝑦2
)
= −2𝑘𝑦0(1 +
∆𝑦
𝑦0
)(1 − [1 +
2𝑦0∆𝑦 + ∆𝑦2
𝑑′2
]
−1/2
)
gunakan ekspansi binomial Newton, yaitu :
(1 + 𝑢)−1/2
= 1 −
1
2
𝑢
𝑑
𝑑′ 𝑦0
∆𝑦
𝑥
𝑥 = √ 𝑑2 + (𝑦0 + ∆𝑦)2
𝑑′
= √ 𝑑2 + 𝑦0
2
𝜃
𝜙

2013(kab/kota)
maka :
[1 +
2𝑦0∆𝑦 + ∆𝑦2
𝑑′2
]
−1/2
= 1 −
1
2
(
2𝑦0∆𝑦 + ∆𝑦2
𝑑′2
)
𝐹𝑝𝑢𝑙𝑖ℎ = −2𝑘𝑦0(1 +
∆𝑦
𝑦0
) (
2𝑦0∆𝑦 + ∆𝑦2
2𝑑′2
)
𝐹𝑝𝑢𝑙𝑖ℎ = −2𝑘
𝑦0
𝑑′2
(
2𝑦0[𝑦0∆𝑦 + ∆𝑦2
] + ∆𝑦2
[𝑦0 + ∆𝑦]
2𝑦0
)
𝐹𝑝𝑢𝑙𝑖ℎ = −2𝑘
𝑦0
2
𝑑′2
∆𝑦 [1 +
∆𝑦
𝑦0
](1 +
∆𝑦
2𝑦0
)
pada diagram di atas :
𝑠𝑖𝑛2
𝜙 =
𝑦0
2
𝑑′2
sehingga :
𝐹𝑝𝑢𝑙𝑖ℎ = −2𝑘𝑠𝑖𝑛2
𝜙∆𝑦 [1 +
3∆𝑦
2𝑦0
+
∆𝑦2
2𝑦0
2
]
untuk :[∴
∆𝑦
𝑦0
≈ 0, 𝑚𝑎𝑘𝑎 ∶ 𝑦0 ≫≫ ∆𝑦]
maka :
∴ 𝐹𝑝𝑢𝑙𝑖ℎ = −2𝑘𝑠𝑖𝑛2
𝜙∆𝑦
benda m dimungkin melakukan gerak harmonis sederhana,
dengan konstanta pembanding sebesar :
𝑘′
= 2𝑘𝑠𝑖𝑛2
𝜙
sehingga :
∴ 𝐹𝑝𝑢𝑙𝑖ℎ + 𝑘′
∆𝑦 = 0
b. besar frekuensinya
kecepatan anguler gerak harmonis berbanding dengan akar
konstanta pembanding dan terbalik dengan massa beban.
𝜔2
=
𝑘′
𝑚
⇋∴ 𝜔 = √
2𝑘𝑠𝑖𝑛2 𝜙
𝑚
∴ 𝑓 =
1
2𝜋
√
𝑚
⇋∴ 𝑇 = 2𝜋√
𝑚

2013(kab/kota)
5. pembahasan
perhatikan perilaku bola billiar sebelum dan sesudah tumbukan
momentum awal dan akhir bola berturut-turut adalah
𝑝1 = −𝑚𝑢
𝑝2 = 𝑚𝑣
impuls merupakan perubahan momentum, maka :
𝐽 = ∆𝑝 = 𝑝2 − 𝑝1
𝐽 = ∆𝑝 = 𝑚𝑣 − (−𝑚𝑢)
𝐽 = ∆𝑝 = 𝑚(𝑣 + 𝑢)
perubahan momentum sudut terjadi karena adanya impuls yang
bekerja pada jarak (h-r) relatif terhadap pusat massa bola,
∆𝐿 = −∆𝑝(ℎ − 𝑟)
∆𝐿 = −𝑚[( 𝑣 + 𝑢)(ℎ − 𝑟)]
∆𝐿 = 𝑚𝑟(𝑣 + 𝑢) − 𝑚ℎ( 𝑣 + 𝑢)
kecepatan sudut awal dan akhir bola berturut-turut adalah
𝜔1 = −
𝑢
𝑟
𝜔2 =
𝑣
𝑟
perubahan momentum sudut bola menjadi
∆𝐿 = 𝐿2 − 𝐿1 = 𝐼(𝜔2 − 𝜔1)
∆𝐿 = 𝐼(
𝑣
𝑟
− [−
𝑢
𝑟
]) = 𝐼(
𝑣 + 𝑢
𝑟
)
dengan momen inersia bola ( 𝐼 =
2
5
𝑚𝑟2
), maka :
∆𝐿 = 𝐼(
𝑣 + 𝑢
𝑟
) =
2
5
𝑚𝑟( 𝑣 + 𝑢)
persamaan hukum kekekalan momentum sudut
𝑚[( 𝑣 + 𝑢)(ℎ − 𝑟)] = −
2
5
𝑚𝑟(𝑣 + 𝑢)
ℎ = 𝑟 −
2
5
𝑟 ∴ ℎ =
3
5
𝑟
ℎ
𝑢
𝑟
𝜔 𝜔
𝑣
ℎ

2013(kab/kota)
6. Pembahasan
garis yang menghubungkan kedua rel sebagai sumbu sesaat
rotasi (AB)
dengan menggunakan dalil pythagoras diperoleh :
(
𝑟
4
)
2
+ ℎ2
= 𝑟2
maka nilai h diperoleh sebesar :
ℎ2
= 𝑟2
− (
𝑟
4
)
2
ℎ =
𝑟√15
4
a. dari data diatas, bahwa gambar tampak depan dan samping
bola yang menggelinding pada dua rel sejajar dan garis AB
sebagai sumbu rotasi sesaat. bahwa ketinggian h diperoleh
sebesar :
∴ ℎ =
𝑟√15
4
dari hasil tersebut bahwa titik yang memiliki kecepatan
maksimum terdapat pada titik yang berjarak terjauh dari
sumbu sesaat. Titik tersebut adalah titik puncak bola.
b. besar kecepatan maksimum diatas jika pusat massa bola
memiliki kecepatan v
kecepatan pusat massa bola adalah v
𝑣 = 𝑣𝑝𝑚
sehingga kecepatan sudut bola menjadi
𝜔 =
𝑣𝑝𝑚
ℎ
=
4𝑣
𝑟√15
𝑟 ℎ
𝑣 𝑚𝑎𝑘𝑠
𝑣𝑝𝑚𝑟
ℎ
𝐴 𝐵
𝑟/4 𝑠𝑎𝑚𝑝𝑖𝑛𝑔𝑑𝑒𝑝𝑎𝑛

2013(kab/kota)
kecepatan sudut di atas selalu sama dengan kecepatan sudut
di puncak bola, maka kecepatan maksimum menjadi :
𝑣 𝑚𝑎𝑘𝑠 = 𝜔(𝑟 + ℎ)
𝑣 𝑚𝑎𝑘𝑠 =
4𝑣
𝑟√15
(𝑟 + 𝑟
√15
4
)
𝑣 𝑚𝑎𝑘𝑠 = (
4 + √15
√15
)𝑣
∴ 𝑣 𝑚𝑎𝑘𝑠 = (4√15+ 1)𝑣
7. Pembahasan
jari-jari setengah bola yang kasar ( 𝑅)
jari-jari bola kecil ( 𝑟) ( 𝑅 > 𝑟)
a. besar kelajuan bola tersebut pada titik terendah, Jika bola
mula-mula diam di titik A dan kemudian menggelinding ke
bawah pada permukaan setengah bola.
dengan ancuan titik dasar bola, energi potensial bernilai nol.
energi mekanik bola di titik A
𝐸𝐴 = 𝑚𝑔𝑅
sudut yang ditempuh oleh bola yang menggelinding adalah
( 𝜙), maka kecepatan bola pada titik terendah ( 𝜙̇), sehingga
kecepatan linier bola titik terendah adalah :
𝑣 = 𝑟𝜙̇
momen inersia bola ( 𝐼 =
2
5
𝑚𝑟2
)
energi potensial bola titik terendah
𝐸 𝑃[𝑟] = 𝑚𝑔𝑟
energi kinetik translasi bola titik terendah
𝐸 𝑘[𝑡𝑟𝑎𝑛𝑠] =
1
2
𝑚𝑣2
=
1
2
𝑚𝑟2
𝜙̇2
energi kinetik rotasi bola titik terendah
𝑠
𝜃
𝑟
𝑅
𝐵 𝐴
𝜙

2013(kab/kota)
𝐸 𝑘[𝑟𝑜𝑡] =
1
2
𝐼𝜙̇2
=
2
5
𝑚𝑟2
𝜙̇2
energi mekanik bola titik terendah adalah :
𝐸 𝑇 = 𝑚𝑔𝑟 +
1
2
𝑚𝑣2
+
1
2
𝐼𝜙̇2
𝐸 𝑇 = 𝑚𝑔𝑟 +
1
2
𝑚𝑣2
+
1
5
𝑚𝑣2
= 𝑚𝑔𝑟 +
7
10
𝑚𝑣2
persamaan hukum kekekalan energi mekanik menjadi
𝑚𝑔𝑅 = 𝑚𝑔𝑟 +
7
10
𝑚𝑣2
𝑔(𝑅 − 𝑟) =
7
10
𝑣2
∴ 𝑣 = √
10𝑔(𝑅 − 𝑟)
7
b. besar periode osilasi, bila berosilasi di sekitar titik terendah
dari pembahasan no. a,
ketika bola berada di titik terendah energi potensial titik
pusat bola sama dengan nol.
panjang busur S yang ditempuh bola adalah
( 𝑅 − 𝑟) 𝜃 = 𝑟 𝜙
𝜙 =
( 𝑅 − 𝑟)
𝑟
𝜃
𝜙̇ =
( 𝑅 − 𝑟)
𝑟
𝜃̇
persamaan energi mekanik ketika membentuk sudut ( 𝜃)
𝐸 𝑇 = 𝑚𝑔ℎ +
1
2
𝑚𝑟2
𝜙̇2
+
2
5
𝑚𝑟2
𝜙̇2
nilai h diperoleh dari jarak titik pusat lingkaran ke titik pusat
bola pada titik terendah
ℎ = ( 𝑅 − 𝑟) − ( 𝑅 − 𝑟) 𝑐𝑜𝑠𝜃 = (𝑅 − 𝑟)(1 − 𝑐𝑜𝑠𝜃)
sehingga :
𝐸 = 𝑚𝑔(𝑅 − 𝑟)(1 − 𝑐𝑜𝑠𝜃) +
1
2
𝑚𝑟2
𝜙̇2
+
2
5
𝑚𝑟2
𝜙̇2
𝐸 = 𝑚𝑔(𝑅 − 𝑟)(1 − 𝑐𝑜𝑠𝜃) +
7
10
𝑚𝑟2
(
( 𝑅 − 𝑟)
𝑟
𝜃̇)
2
𝐸 = 𝑚𝑔(𝑅 − 𝑟)(1 − 𝑐𝑜𝑠𝜃) +
7
10
𝑚( 𝑅 − 𝑟)2
𝜃̇2

2013(kab/kota)
defferensial energi terhadap waktu, sama dengan nol
𝑑𝐸
𝑑𝑡
= 0
𝑑
𝑑𝑡
{ 𝑚𝑔(𝑅 − 𝑟)(1 − 𝑐𝑜𝑠𝜃) +
7
10
𝑚( 𝑅 − 𝑟)2
𝜃̇2} = 0
𝑔(𝑅 − 𝑟)𝑠𝑖𝑛𝜃 +
7
5
( 𝑅 − 𝑟)2
𝜃̈ = 0
pada simpangan sudut kecil ( 𝑠𝑖𝑛𝜃 = 𝜃)
𝑔𝜃 +
7
5
( 𝑅 − 𝑟) 𝜃̈ = 0
𝜃̈ +
5𝑔
7( 𝑅 − 𝑟)
𝜃 = 0
𝜃̈ + 𝜔2
𝜃 = 0
kecepatan sudut yang diperoleh menjadi
𝜔2
=
5𝑔
7( 𝑅 − 𝑟)
∴ 𝜔 = √
5𝑔
7( 𝑅 − 𝑟)
periode osilasi karena bola bergerak sebagai persamaan
gerak harmonis adalah :
∴ 𝑇 = 2𝜋√
7( 𝑅 − 𝑟)
5𝑔
atau frekuensi osilasinya
∴ 𝑓 =
1
2𝜋
√
5𝑔
7( 𝑅 − 𝑟)

2013(kab/kota)
8. Pembahasan
peristiwa di atas bahwa tidak ada torsi luar atau gangguan dari
luar terhadap sistem, maka momentum sudut awal sama
dengan nol
𝐿 𝑎𝑤𝑎𝑙 = 0
( 𝑚 𝐿) adalah massa lokomotif mainan dengan kecepatan
lokomotif relatif terhadap tanah ( 𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ )
( 𝑚 𝑇) adalah massa total lintasan melingkar (pelek) dengan
kecepatan linier relatif terhadap tanah ( 𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ )
sehingga momentum akhir adalah :
𝐿 𝑎𝑘ℎ𝑖𝑟 = 𝐼 𝑇 𝜔 𝑇 + 𝐼𝐿 𝜔𝐿
𝐿 𝑎𝑘ℎ𝑖𝑟 = 𝐼 𝑇 (
𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ
𝑅
) + 𝐼𝐿 (
𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ
𝑅
)
dengan ( 𝐼 𝑇 = 𝑚 𝑇 𝑅2
𝑑𝑎𝑛 𝐼𝐿 = 𝑚 𝐿 𝑅2
)
maka :
𝐿 𝑎𝑘ℎ𝑖𝑟 = 𝑚 𝑇 𝑅2
(
𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ
𝑅
)+ 𝑚 𝐿 𝑅2
(
𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ
𝑅
)
𝐿 𝑎𝑘ℎ𝑖𝑟 = 𝑚 𝑇 𝑅𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ + 𝑚 𝐿 𝑅𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ
hukum kekekalan momentum sudut menjadi
𝑚 𝑇 𝑅𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ + 𝑚 𝐿 𝑅𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ = 0

2013(kab/kota)
kecepatan total sistem terhadap tanah adalah ( 𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ ) jumlah
aljabar dari kecepatan lokomotif mainan terhadap tanah
( 𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ) dan kecepatan akhir lokomotif terhadap lintasan
𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ = 𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ + 𝑣
sehingga :
𝑚 𝑇 𝑅𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ + 𝑚 𝐿 𝑅𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ = 0
∴ 𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ = −
𝑚 𝑇 𝑣
( 𝑚 𝑇 + 𝑚 𝐿)
kecepatan akhir lokomofit relatif terhadap lantai ( 𝑣𝑓) sama
dengan kecepatan lokomotif relatif terhadap tahan ( 𝑣 𝑇.𝑡𝑎𝑛𝑎ℎ ),
maka :
∴ 𝑣𝑓 = 𝑣 𝐿.𝑡𝑎𝑛𝑎ℎ = −
𝑚 𝑇 𝑣
( 𝑚 𝑇 + 𝑚 𝐿)
bertanda negatif karena arah gerak lokomotif berlawanan
dengan arah gerak rel

2013 osnk fisika (tkunci)

More Related Content

What's hot

Similar to 2013 osnk fisika (tkunci)

More from SMA Negeri 9 KERINCI

Recently uploaded

2013 osnk fisika (tkunci)