The document by Saad Haj Bakry provides an extensive overview of basic statistics applicable to system studies, covering topics such as statistical distributions, random number generation, and confidence intervals. It elaborates on different statistical measures including mean, mode, median, variance, and distributions like binomial and normal. Additionally, it includes practical algorithms and software functions necessary for data processing and analysis in statistics.

1. 1
SAAD HAJ BAKRY, PhD, CEng, FIEESAAD HAJ BAKRY, PhD, CEng, FIEE
BASIC STATISTICS
FOR SYSTEM STUDIES
BASIC STATISTICS
FOR SYSTEM STUDIES

2. 2
OBJECTIVES / CONTENTSOBJECTIVES / CONTENTS
Saad Haj Bakry
STATISTICAL DISTRIBUTIONSSTATISTICAL DISTRIBUTIONS
GENERATION OF RANDOM NUMBERSGENERATION OF RANDOM NUMBERS
CONFIDENCE INTERVALSCONFIDENCE INTERVALS
Basic Statistics
REQUIRED DEVELOPMENTREQUIRED DEVELOPMENT

3. 3
FREQUENCY DISTRIBUTION: 1/3FREQUENCY DISTRIBUTION: 1/3
Saad Haj Bakry
Statistical Distributions
INPUT: raw data “a set of (N) values”INPUT: raw data “a set of (N) values”
ORGANIZE: values in ascending / descending
order
ORGANIZE: values in ascending / descending
order
DETERMINE: the range of raw data / valuesDETERMINE: the range of raw data / values
DIVIDE: the range into sub-rangesDIVIDE: the range into sub-ranges
Basic Statistics

4. 4
FREQUENCY DISTRIBUTION: 2/3FREQUENCY DISTRIBUTION: 2/3
Saad Haj Bakry
Statistical Distributions
FIND: number of values per sub-range “frequency”FIND: number of values per sub-range “frequency”
RESULT: frequency distributionRESULT: frequency distribution
DIVIDE: frequency of each sub-range by (N)DIVIDE: frequency of each sub-range by (N)
RESULT: relative frequency distribution
“probability density”
RESULT: relative frequency distribution
“probability density”
Basic Statistics

5. 5
FREQUENCY DISTRIBUTION: 3/3FREQUENCY DISTRIBUTION: 3/3
Saad Haj Bakry
Statistical Distributions
ADD: frequencies sub-range by sub-rangeADD: frequencies sub-range by sub-range
RESULT: cumulative frequency distributionRESULT: cumulative frequency distribution
ADD: relative frequencies sub-range by sub-rangeADD: relative frequencies sub-range by sub-range
RESULT: relative cumulative frequency
distribution “cumulative probability”
RESULT: relative cumulative frequency
distribution “cumulative probability”
Basic Statistics

6. 6
FREQUENCY DISTRIBUTION: ProblemFREQUENCY DISTRIBUTION: Problem
Saad Haj Bakry
Statistical Distributions
Given: “N values” raw data
(N is very large for probability considerations(
Find
(Graphs to
Illustrate(
Frequency Distribution
Relative Frequency Distribution:
(Probability Density(
Cumulative Frequency Distribution
Relative Cumulative Frequency
Distribution
(Cumulative Probability(
Basic Statistics

7. 7
Saad Haj Bakry
MEAN : AVERAGE : EXPECTATIONMEAN : AVERAGE : EXPECTATION
Statistical Distributions
Definition Arithmetic mean
Raw Data Given values: x[1], x[2], …. x[N[
Mean m=
Raw Data
Given ranges: y[1], y[2], ….y[n[
Frequencies: f[1], f[2], …. f[n[
Weighted
Mean
m= :
Problem Write and test computer functions /
Give Illustrations
][].[
1
1
∑
=
=
nj
j
jyjf
N
∑
=
=
Ni
i
ix
N 1
][
1
∑
=
=
=
nj
j
Njf
1
][
Basic Statistics

8. 8
Saad Haj Bakry
MODE / MEDIANMODE / MEDIAN
Statistical Distributions
Median Middle value
Mode Value with highest frequency
Raw Data Given values: x[1], x[2], …. x[N]
Median
For ODD N: m = x[(N+1)/2]
EVEN: m = (1/2) {x[N/2]+x[(N/2)+1]}
Mode
Find frequency distribution:
m = x[k] : f[k] highest frequency
Problem Write and test computer functions /
Give Illustrations
Basic Statistics

9. 9
Saad Haj Bakry
DEVIATION / VARIANCEDEVIATION / VARIANCE
Statistical Distributions
Deviation
Deviation from the “mean”
d[i] = |x[i] – m|
Mean
Deviation
Variance /
Standard
Deviation
Standard
Score
Standardized Variables: z[i] = d[i] / s
Problem Write and test computer functions /
Give Illustrations
∑
=
=
=
Ni
i
id
N
d
1
][
1
∑=
=
n
j
jdjf
n
d
1
][].[
1
∑
=
=
=
nj
j
Njf
1
][
∑
=
=
=
Ni
i
idN
v
1
2
][
1
vs =
Basic Statistics

10. 10
Saad Haj Bakry
UNIFORM DISTRIBUTIONUNIFORM DISTRIBUTION
Statistical Distributions
Features
Range
“min”: Minimum number
“max”: Maximum number
Principle All numbers “x[i] : x” are equally likely
Probability Density p(x,min,max) = 1 / (max-min(
Mean m = (max + min) / 2
Variance v = (max - min)2
/ 12
Problem Write and test computer functions /
Give Illustrations
Basic Statistics

11. 11
Saad Haj Bakry
BINOMIAL DISTRIBUTIONBINOMIAL DISTRIBUTION
Statistical Distributions
Features
N Number of trials
p Probability of success
q Probability of failure: q = 1 - p
x Number of successful trials in N
Probability Density
Mean m = N . p
Variance v = N . p . q
Problem Write and test computer functions /
Give Illustrations
qpC
xNxN
x
pNxp
−
=(,,(
Basic Statistics

12. 12
Saad Haj Bakry
POISSON DISTRIBUTIONPOISSON DISTRIBUTION
Statistical Distributions
Features
r Rate of arrivals: mean
t Time interval, may be “t=1 time unit”
x Possible number of arrivals during “t”
Probability Density
Mean m = r
Variance v = r
Problem Write and test computer functions /
Give Illustrations
rt
x
e
x
rt
trxp −
=
!
((
(,,(
Basic Statistics

13. 13
Saad Haj Bakry
EXPONENTIAL DISTRIBUTIONEXPONENTIAL DISTRIBUTION
Statistical Distributions
Features
r Rate of arrivals
w Waiting time for next arrival: Inter-arrival
Principle Distribution for the value of “w”
Probability Density
Mean m = 1 / r (Poisson inter-arrival mean(
Variance v = 1 / r2
Problem Write and test computer functions /
Give Illustrations
rw
errwp −
= .(,(
Basic Statistics

14. 14
Saad Haj Bakry
NORMAL DISTRIBUTIONNORMAL DISTRIBUTION
Statistical Distributions
Features
Range - (infinity) < x < + (infinity)
m Average value: mean / median / mode
v Variance: v = s2
x Possible value
Principle Usually a measurement process
Probability Density
Standard form:
Problem Write and test computer functions /
Give Illustrations
2
2
((
2
1
2
1
(,,(
mx
s
e
s
smxp
−−
=
π
2
2
1
2
1
(1,0,(
z
ezp
−
=
π
Basic Statistics

15. 15
Saad Haj Bakry
t DISTRIBUTIONt DISTRIBUTION
Statistical Distributions
Features
Range - (infinity) < t < + (infinity)
m mean / median / mode at “zero”
f Degree of freedom: 0 < f < + (infinity(
Principle Used for estimation: small sample
t Distribution variable: variance unknown
Probability Density
Gamma Function
Problem Write and test computer functions /
Give Illustrations
2/(1(
2
(1(
(2/(
]2/(1[(
(,( +−
+
Γ
+Γ
= f
f
t
ff
f
ftp
π
(!1(((
0
1
−==Γ −
∞
−
∫ fdxexf xf
Basic Statistics

16. 16
Saad Haj Bakry
COMPUTATION TIPS: 1/2COMPUTATION TIPS: 1/2
Statistical Distributions
Integer Factorial
0 ! = 1
(i+1) ! = i! (i+1(
Real Factorial
Sterling Formula:
Gamma Function Useful for its computation
Problem Write and test computer functions /
Give Illustrations
ii
eiii −
≈ π2!
Basic Statistics

17. 17
Saad Haj Bakry
Statistical Distributions
i
iN
CC N
i
N
i
)1(
1
+−
=+
Combination
Poisson
Integration Trapezoid Rule: Summation in small steps
Problem Write and test computer functions /
Give Illustrations
1
!0
0
=
A
10 =N
C
)1(!)!1(
1
+
=
+
+
i
A
i
A
i
A ii
COMPUTATION TIPS: 2/2COMPUTATION TIPS: 2/2
Basic Statistics

18. 18
RNGS: WHYRNGS: WHY
Saad Haj Bakry
SYSTEM
MODELING /
SIMULATION
SYSTEM
MODELING /
SIMULATION
SAMPLINGSAMPLING
NUMERICAL ANALYSISNUMERICAL ANALYSISRANDOM
PROCESSES
RANDOM
PROCESSES
TESTING
COMPUTER
ALGORITHMS
TESTING
COMPUTER
ALGORITHMS
DECISION
MAKING
DECISION
MAKING
OTHER REASONSOTHER REASONS
Generation of Random NumbersBasic Statistics

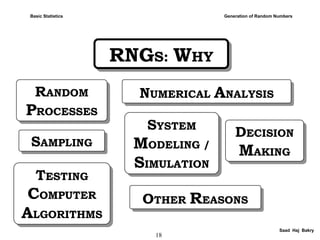
19. 19
Saad Haj Bakry
UNIFORM RNG: U (0,1)UNIFORM RNG: U (0,1)
Features
m
Modulus factor: large (st) prime number within
memory cell size (for wide repeated sequence cycle(
m = 231
- 1 = 2,147,483,674 (for 32 bit cell(
a Multiplier: a = 314,159,269
b Increment: b = 453,806,245
X[0[ Starting value: X[0] = 577,215,665 (the seed)
X[i-1[ “)ith-1)” value: seed for X[i[
Uniform: X (0,m( X[i] = {a . X[i-1] + b} MOD m
Uniform: U (0,1( U[i] = X[i] / m
Problem Write and test computer functions /
Give Illustrations
Generation of Random NumbersBasic Statistics

20. 20
Saad Haj Bakry
UNIFORM RNG: U (min , max)UNIFORM RNG: U (min , max)
Integer
Range
min Required minimum integer value
max Required maximum integer value
U (min, max( min + TRUNC [(max – min + 1) . U (0, 1([
Problem Write and test computer functions /
Give Illustrations
Test
100,000“runs”: Test
• Frequency Distribution
• Mean
• Variance & Standard Deviation
)Relative to theoretical expectations(
Note Every new set of runs should start with
a different seed: X[0]
Generation of Random NumbersBasic Statistics

21. 21
Saad Haj Bakry
EXPONENTIAL RNG: E (m)EXPONENTIAL RNG: E (m)
Required “mean”:
“inter-event” Poisson
m
E (mean( - )m) . Ln [U(0, 1([
Problem Write and test computer
functions / Give Illustrations
Test
100,000“runs”: Test
• Frequency Distribution
• Mean
• Variance & Standard Deviation
)Relative to theoretical
expectations(
Generation of Random NumbersBasic Statistics

22. 22
Saad Haj Bakry
NORMAL RNG: N (m, s)NORMAL RNG: N (m, s)
Features
m Required “mean” of the normal RNG
s Required “standard deviation”
STEPS
1
V[1] = 2 . { U(0,1)[1] } – 1
V[2] = 2 . { U(0,1)[2] } – 1
2 SUM = V2
[1] + V2
[2[
3 IF SUM >= 1 GO TO STEP 1
4
5 N (m,s) = m + s . Y
Standard Normal N (0,1) = Y
Problem Write and test computer functions /
Give Illustrations
SUMSUMLnVY /)](.2[].2[ −=
Generation of Random NumbersBasic Statistics

23. 23
Saad Haj Bakry
ConfidenceBasic Statistics
MEASUREMENTS & ESTIMATIONSMEASUREMENTS & ESTIMATIONS
MEASUREMENTS: Experiments on real
systems / models / Simulation
MEASUREMENTS: Experiments on real
systems / models / Simulation
Confidence
for
“Mean”
ESTIMATION
THEORY
ESTIMATION
THEORY
SET OF VALUES: Sample of results (N)SET OF VALUES: Sample of results (N)
Confidence
for
“Sample”
Large Sample: N >= 30 Small Sample: N < 30

24. 24
Saad Haj Bakry
EVALUATION ALGORITHM: GeneralEVALUATION ALGORITHM: General
Confidence IntervalsBasic Statistics
INPUT: Measurements: N & x[1], x[2],….,x[N]
Required “confidence level” : L (%)
INPUT: Measurements: N & x[1], x[2],….,x[N]
Required “confidence level” : L (%)
MEAN: |MEAN: | ∑
=
=
=
Ni
i
ix
N
m
1
][
1
STANDARD DEVIATION:|STANDARD DEVIATION:| ∑
=
=
−
−
=
ni
i
mix
N
s
1
2
}][{
1
1
AREA UNDER CURVE: | a = 1 – (L/100)AREA UNDER CURVE: | a = 1 – (L/100)

25. 25
Saad Haj Bakry
NORMAL DISTRIBUTIONNORMAL DISTRIBUTION
Confidence IntervalsBasic Statistics
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
3.9 -3 -2 -1 -0.5 0 0.5 1 2 3 3.9
Probability
Density
Mean
Standard
Deviations
68.27 %
95.45 %
- z (a/2) + z (a/2)
Standard
Deviations

26. 26
Saad Haj Bakry
EVALUATION ALGORITHM: N >=30EVALUATION ALGORITHM: N >=30
Confidence IntervalsBasic Statistics
| m – (Z (a/2) . S) < sample < m – (Z (a/2) . S)| m – (Z (a/2) . S) < sample < m – (Z (a/2) . S)
CONFIDENCE COEFFICIENT: Z (a/2)
|
CONFIDENCE COEFFICIENT: Z (a/2)
| ∫
−
=
−
)2/(
2
0
2
2
2
2
1
aZ z
dze
a
π
|| N
S
Zmmean
N
S
Zm aa )2/()2/( +<<−

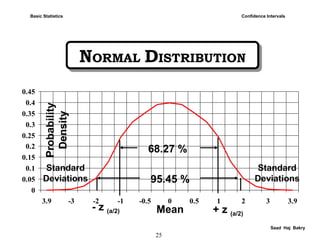
27. 27
Saad Haj Bakry
EVALUATION ALGORITHM: N < 30EVALUATION ALGORITHM: N < 30
Confidence IntervalsBasic Statistics
| m – (T (a/2) . S) < sample < m – (T (a/2) . S)| m – (T (a/2) . S) < sample < m – (T (a/2) . S)
|| ∫
−
−
+
−−Γ
Γ
=
−
)2/(
0
)2/(
2
)
1
1(
)1(]2/)1[(
)2/(
2
1
aT
N
dt
N
t
NN
Na
π
|| N
S
Tmmean
N
S
Tm aa )2/()2/( +<<−
|| )!1(.)(
0
1
−==Γ ∫
∞
−−
fdxexf xf

28. 28
SOFTWARE FUNCTIONS: 1/4SOFTWARE FUNCTIONS: 1/4
Saad Haj Bakry
Basic Statistics Required Development
SUBJECT FUNCTION INPUT OUTPUT
Frequency Distribution
(Raw Data: Empirical
Distributions(
“N: Integer”: Number of values
“Array of N values: Real Array”
“n: Integer”: Number of ranges
“Array of n ranges: Real Array”
Array of n frequencies:
Integer Array”
Central
Measures
Mean “N: Integer”: Number of values
“Array of N values: Real Array”
)Can also be considered with
frequency ranges(
“Mean value: Real”
Median “Median: Real”
Mode “Mode: Real”
Dispersion
Measures
Mean
Deviation As above
)May be with Mean: Real(
)It can also be: Variance for
Standard Deviation and Vice
Versa(
“Average Deviation:
Real”
Variance “Variance: Real”
Standard
Deviation
“Standard Deviation:
Real”

29. 29
SOFTWARE FUNCTIONS: 2/4SOFTWARE FUNCTIONS: 2/4
Saad Haj Bakry
Basic Statistics Required Development
SUBJECT FUNCTION INPUT OUTPUT
Binomial
Distribution
Combination
“N: Integer”: Number of values
(objects / independent trails)
“X: Integer”: Number of selected
values (success)
“Value of
Combination:
Real”
Probability
Density
As above plus:
“p: Real”: probability of success
“Probability of X
successes: Real”
Cumulative
Probability
“N, p”: As above.
“X1-X2: integers”: Range values
“Sum of
probabilities
(range): Real”
Poisson
Distribution
Probability
Density
“X: Integer”: Number of (arrivals(
“m: Real”: Mean number of (arrivals(
“Probability of X
arrivals: Real”
Cumulative
Probability
“m”: As above.
“X1-X2: Integers”: Range values
“Sum of
probabilities
(range): Real”

30. 30
SOFTWARE FUNCTIONS: 3/4SOFTWARE FUNCTIONS: 3/4
Saad Haj Bakry
Basic Statistics Required Development
SUBJECT FUNCTION INPUT OUTPUT
Standard
Normal
Distribution
Probability
Density
“z: Real”: Random variable
(measurement(
“Probability of value
z: Real”
Cumulative
Probability
“z1-z2: Real”: Range of values
“Sum of probabilities
(range): Real”
Gamma
Function
“f: Integer”: Degree of freedom “Value of
gamma function:
Real”
“f: Real”: Degree of freedom
“f: Integer or Real”: Degree of freedom
T-
Distribution
Probability
Density
“f: Integer or Real”
“t: Real”: Random variable
“Probability of value
t: Real”
Cumulative
Probability
“f1-f2: Real”: Range of values
“Sum of probabilities
(range): Real”

31. 31
SOFTWARE FUNCTIONS: 4/4SOFTWARE FUNCTIONS: 4/4
Saad Haj Bakry
Basic Statistics Required Development
SUBJECT FUNCTION INPUT OUTPUT
Confidence
Co-efficient
For Large
Sample
“L: Real”: Level of
Confidence (%)
Z(a/2): Real
For Small
Sample
“L”: As above.
“N: Integer”: Sample size
T(a/2): Real
Random
Number
Generators
Uniform “Seed: Real / Integer” :
According to requirements
“Uniform random value
(0-1): Real”
U (min, max( “Min, Max: Integers”:
Range
“Uniform random value
in the range: Integer”
E (m( “m: Real”: Mean value
(duration(
“Exponential random
value of mean m: Real”
N (m, s(
“m: Real”: Mean value
(measure(
“s: Real”: Standard
deviation
“Normal random value
of mean m, and standard
deviation s: Real”

32. 32
REFERENCESREFERENCES
Saad Haj Bakry
Seq.
Authors /
References
Title Publication
1 Murray R Spiegel Statistics
Schaum’s Outline Series,
McGraw-Hill, 1972
2
Ronald E. Walpole
Raymond H. Myers
Probability and Statistics for
Engineers & Scientists
Collier Macmillan, 1972
Donald E. Knuth
The Art of Computer Programming,
Vol.2
Addison-Wesley, 1969
4
Saad Haj Bakry and
Mustafa Shatila
Pascal Functions for the
Generation of Random Numbers
Journal of Computer,
Mathematics & Applications,
Vol. 15, No. 11, pp. 969-973,
1988 Pergamon Press, UK
5
Saad Haj Bakry and
Mustafa Shatila
A Computer Algorithm for Comp
the Confidence Limits of Measured
Factors
Journal of Engineering
Science, KSU, Vol. 2,
1990, pp. 195-200
6
Averill M. Law
W. David Kelton
Simulation Modeling and Analysis McGraw-Hill, 2000
Basic Statistics