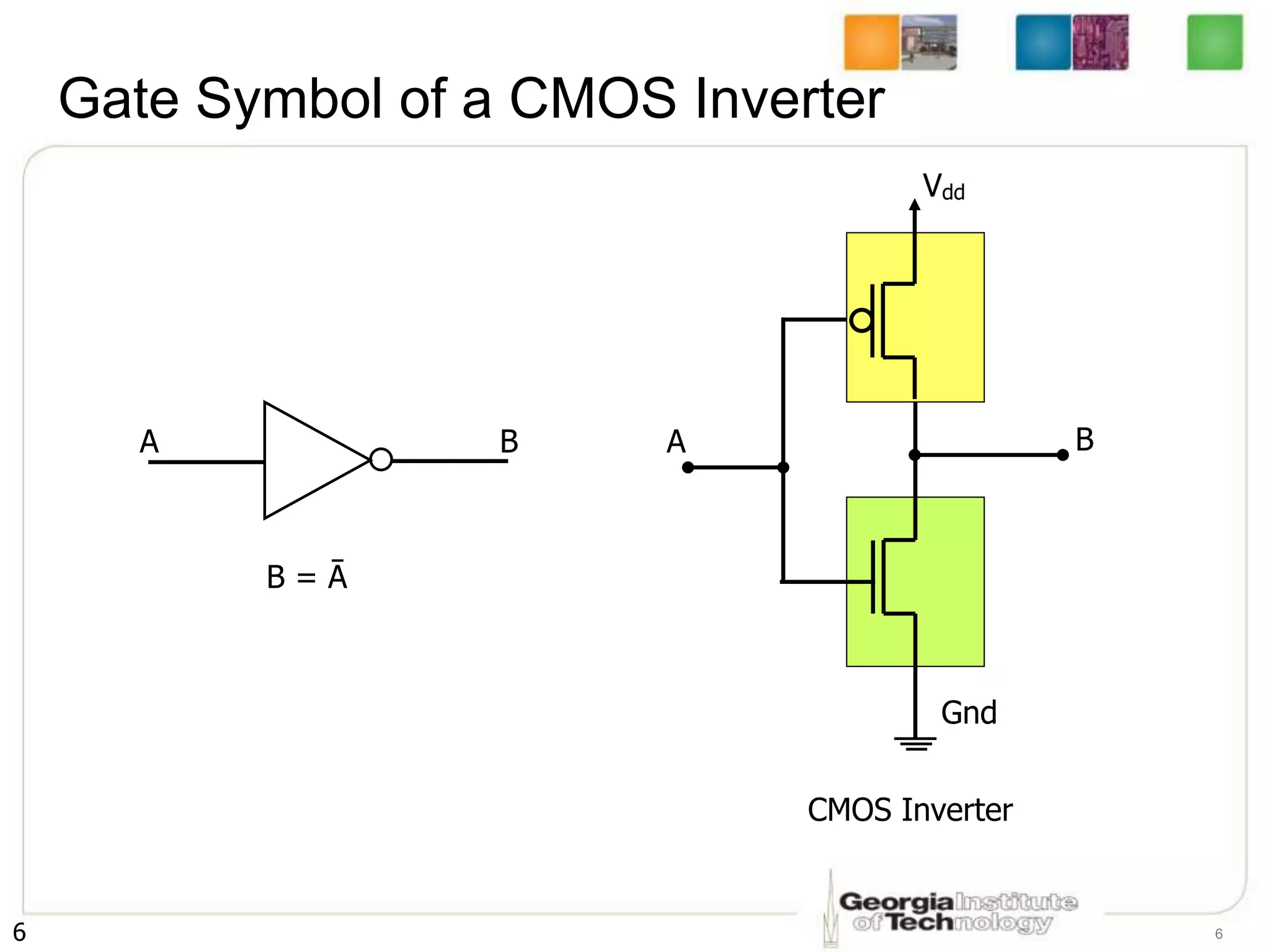
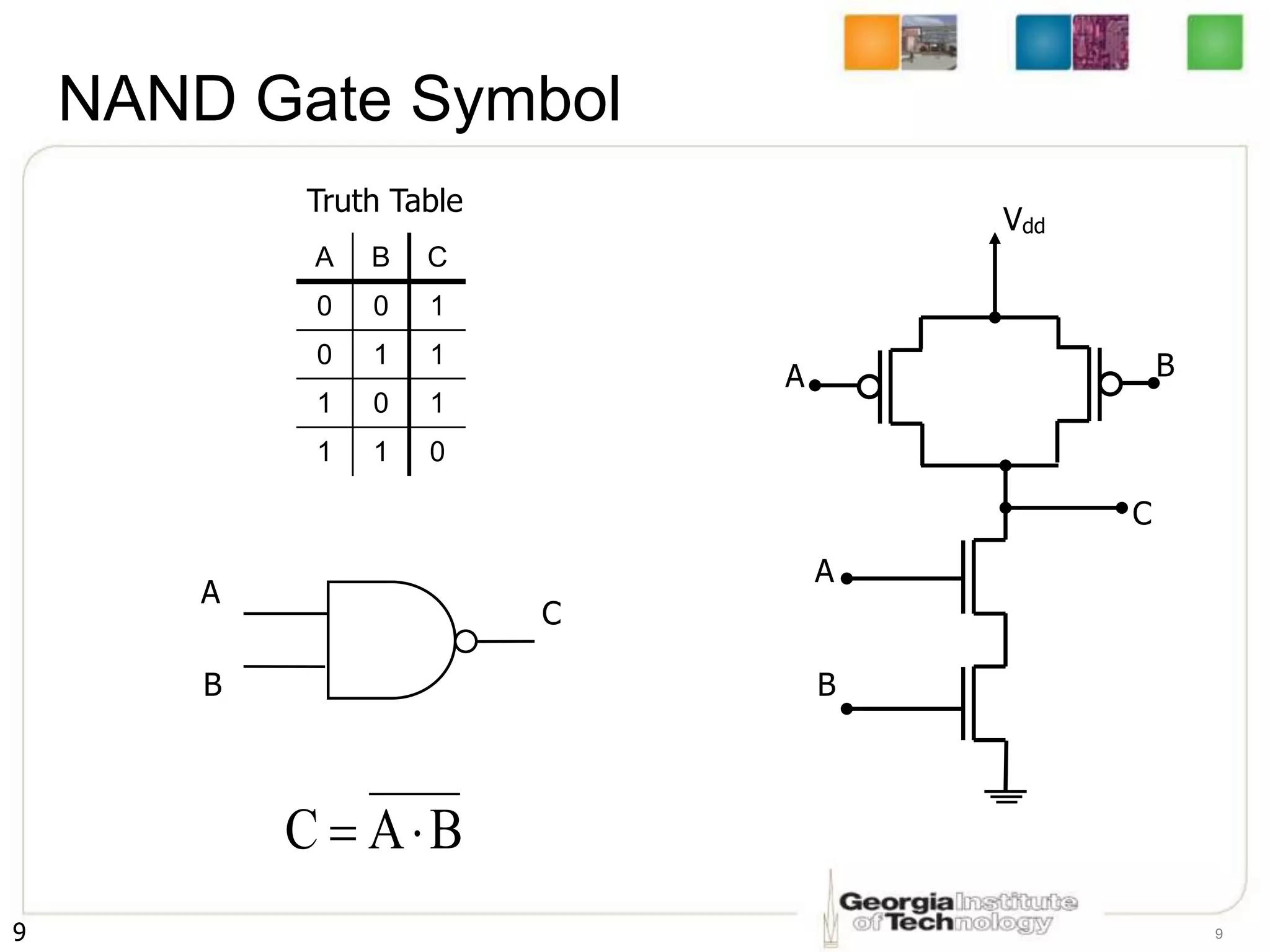
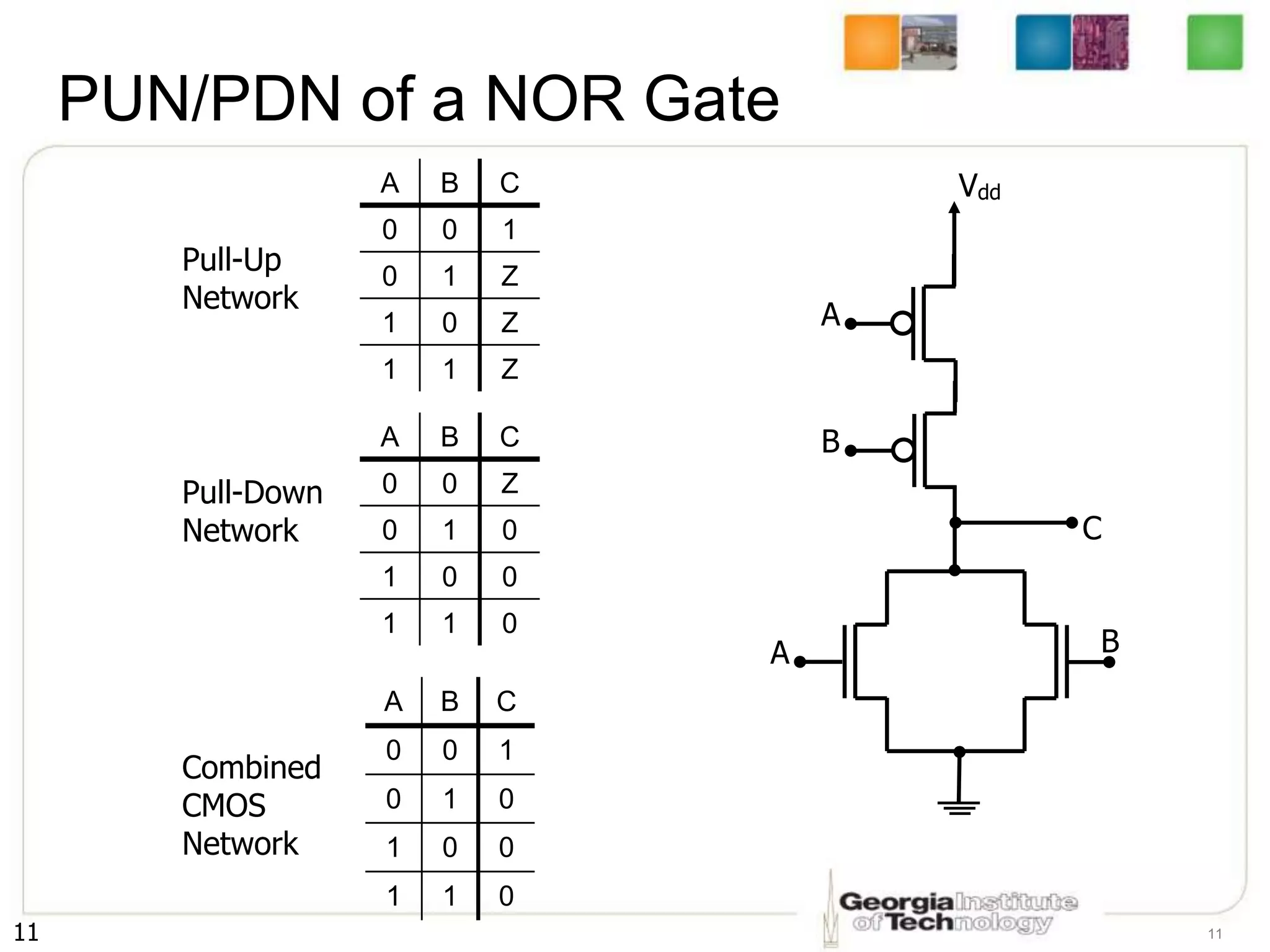
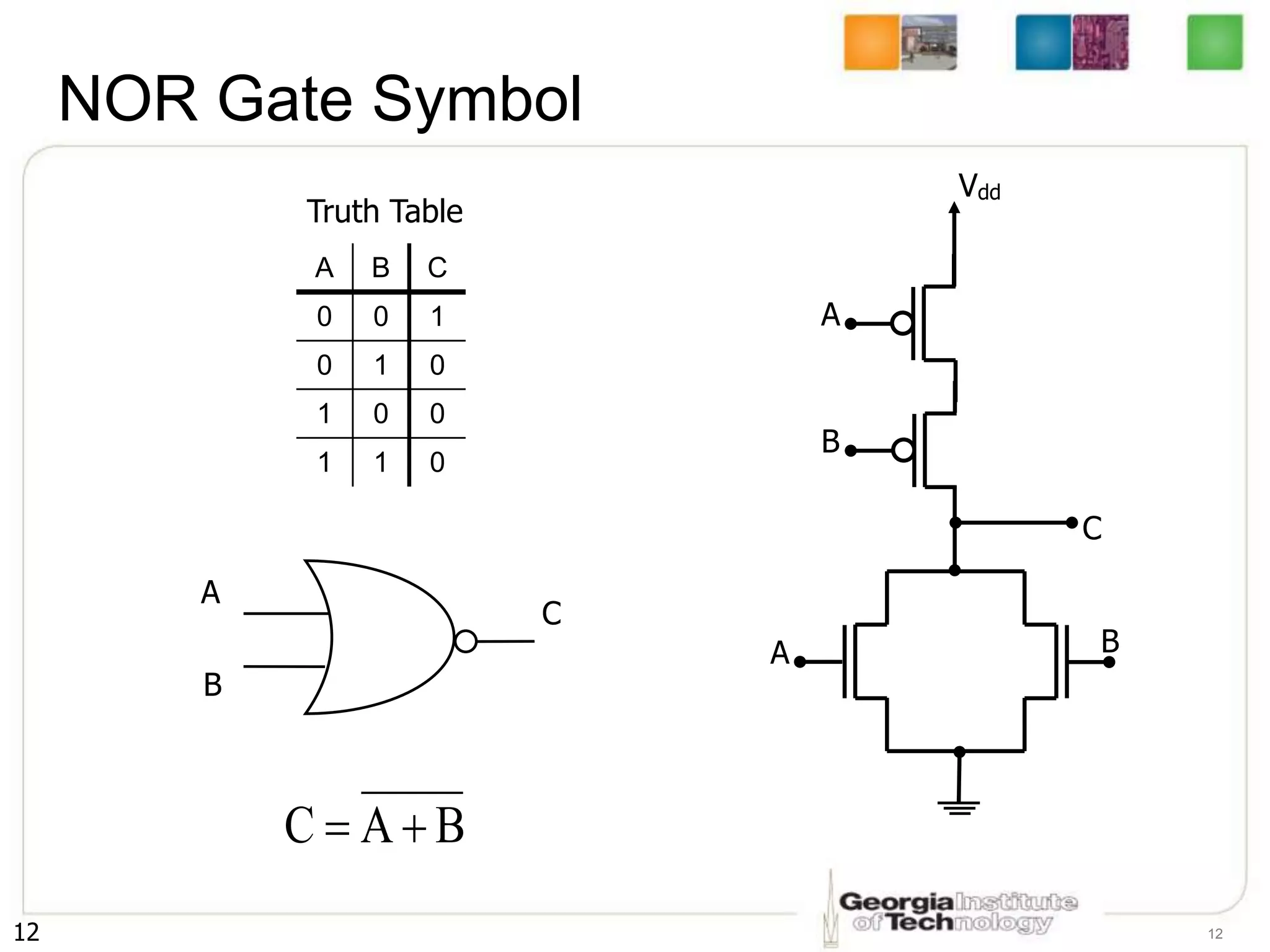
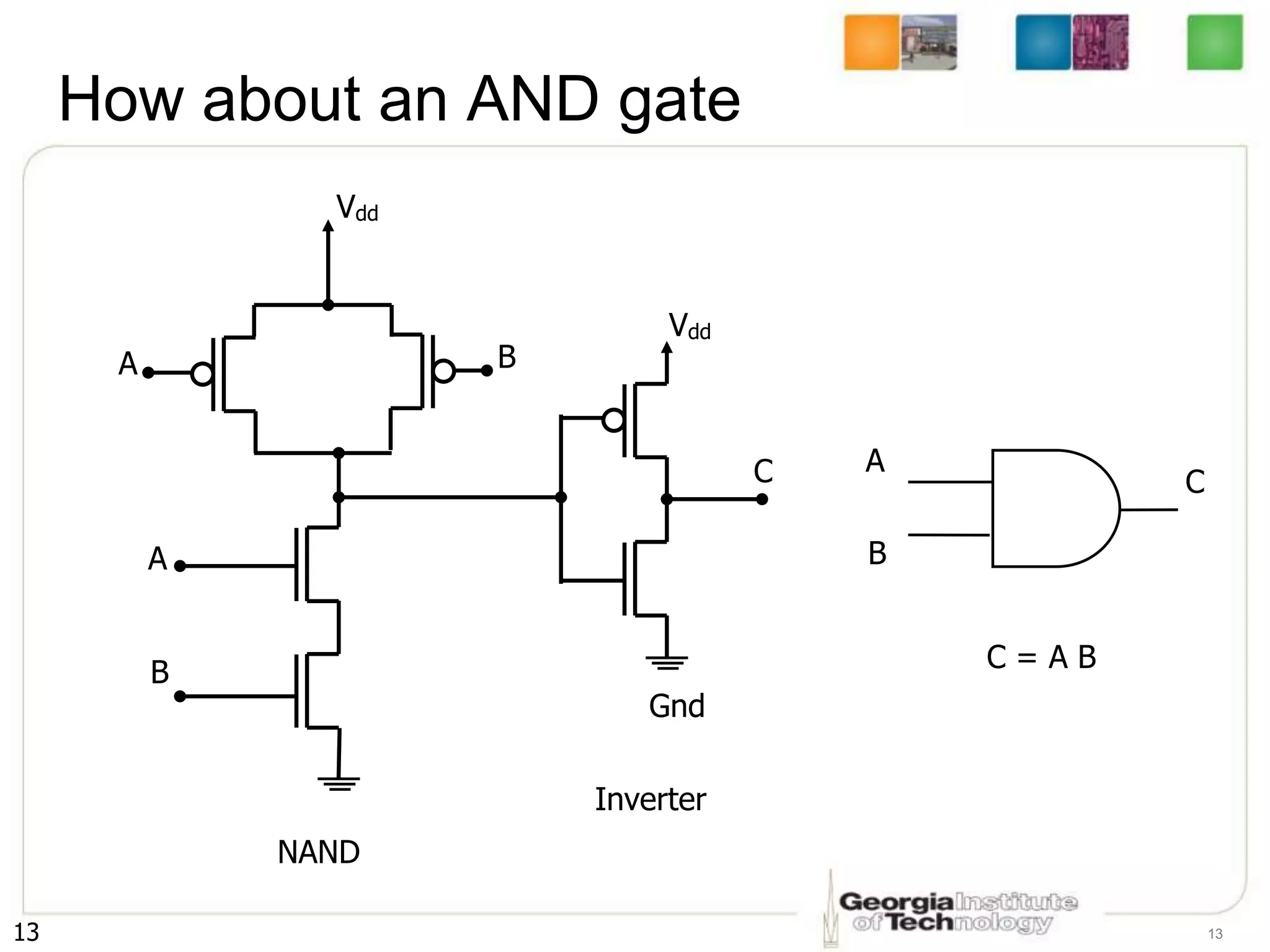
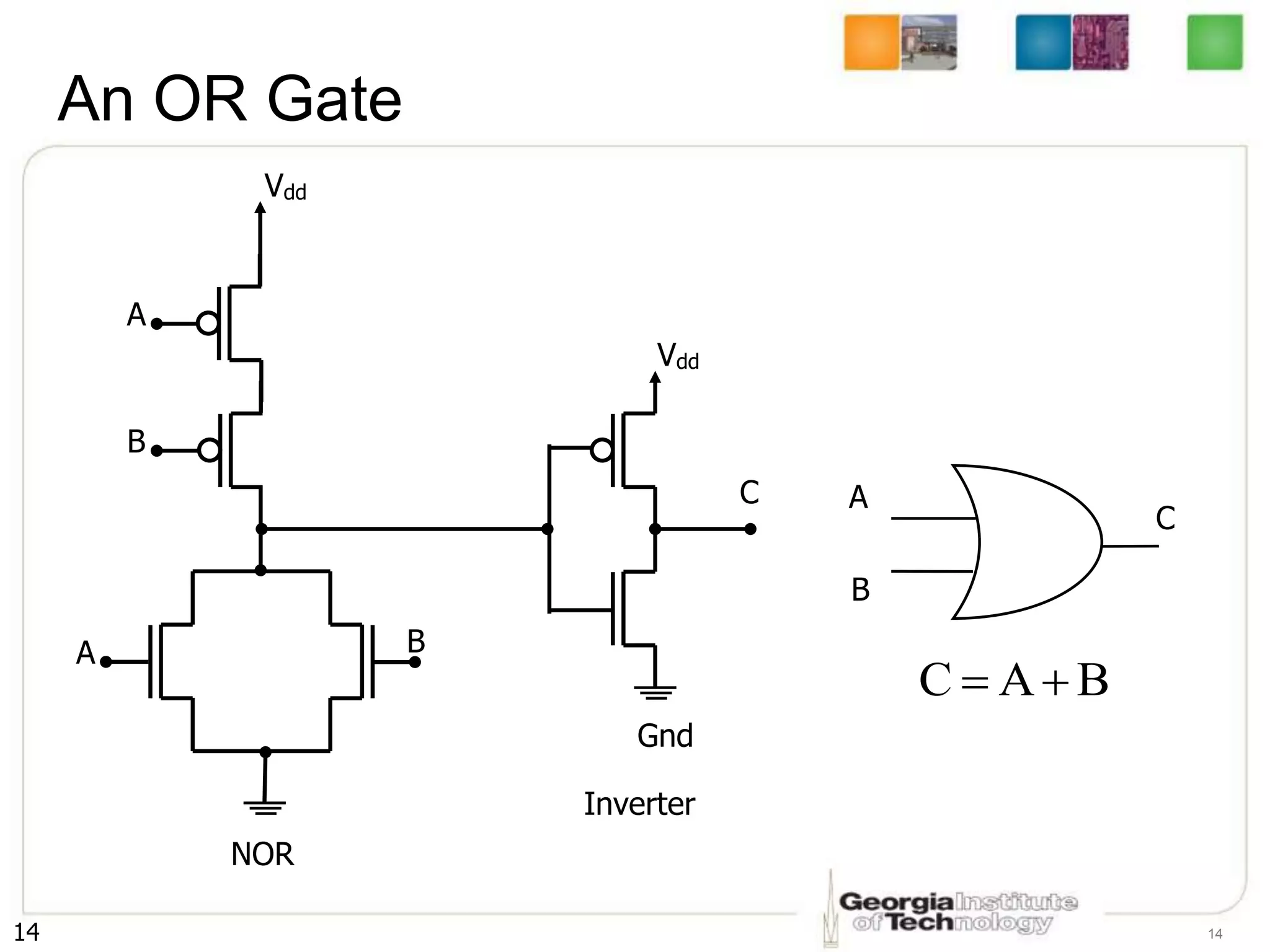
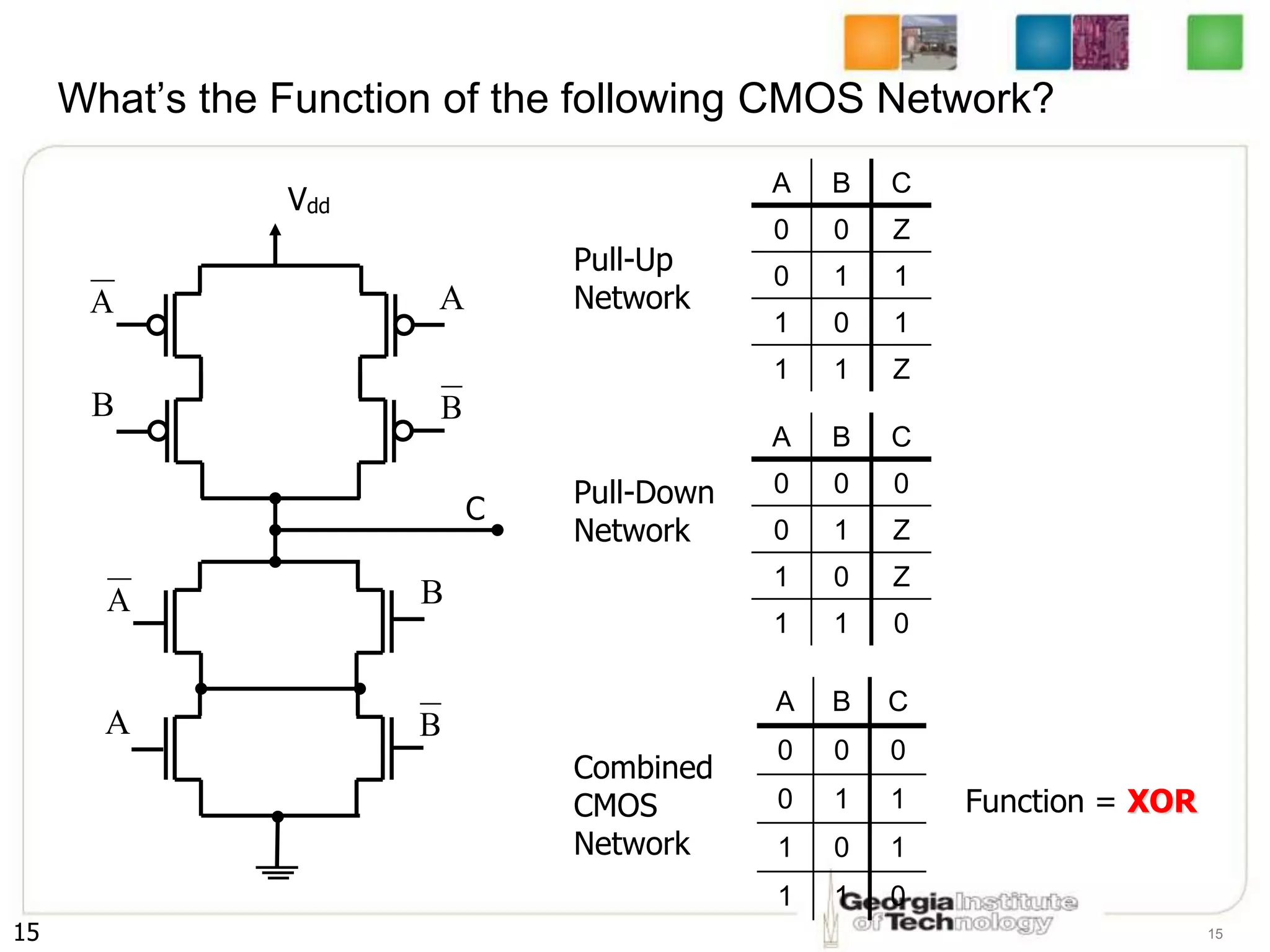
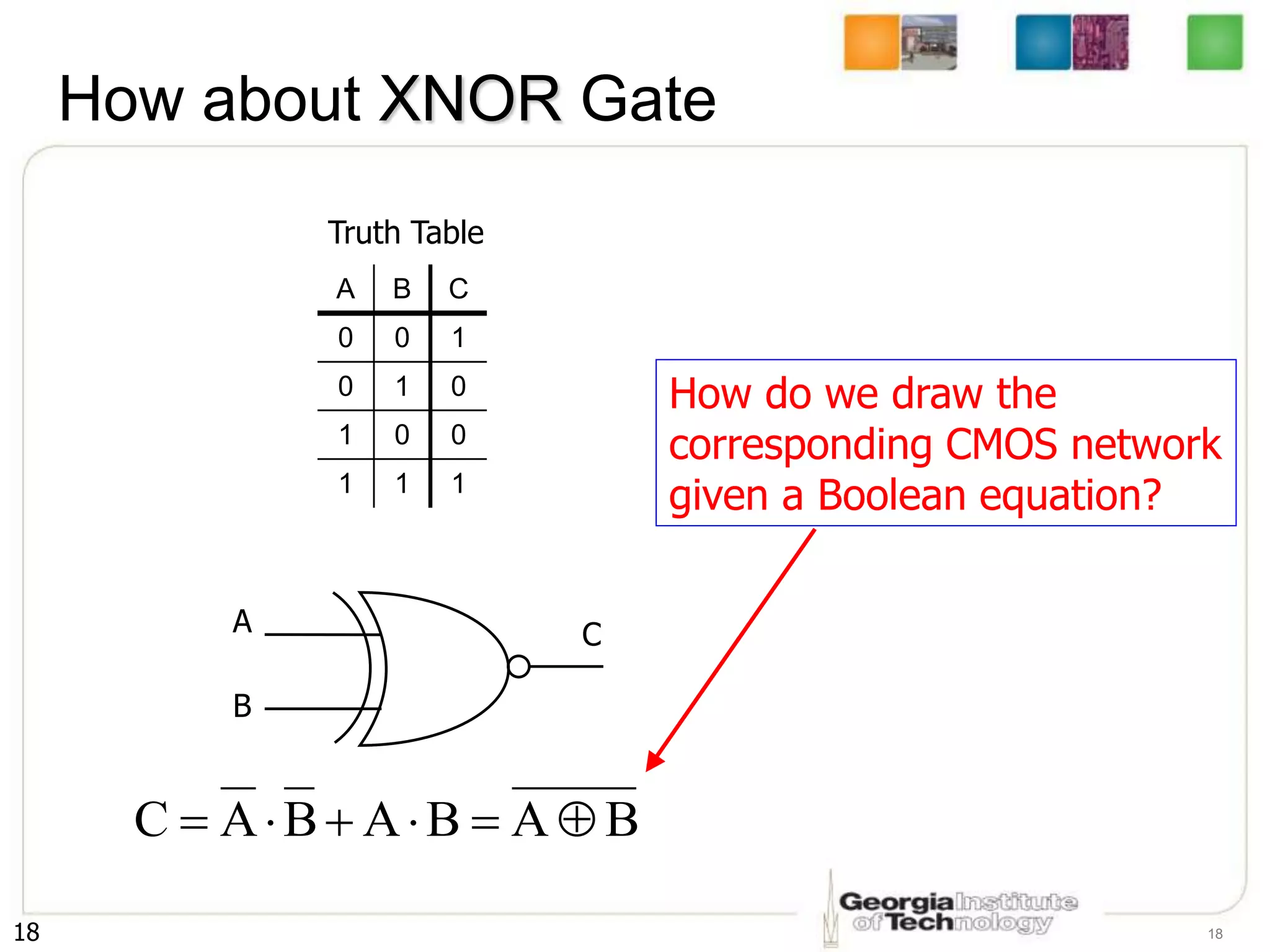
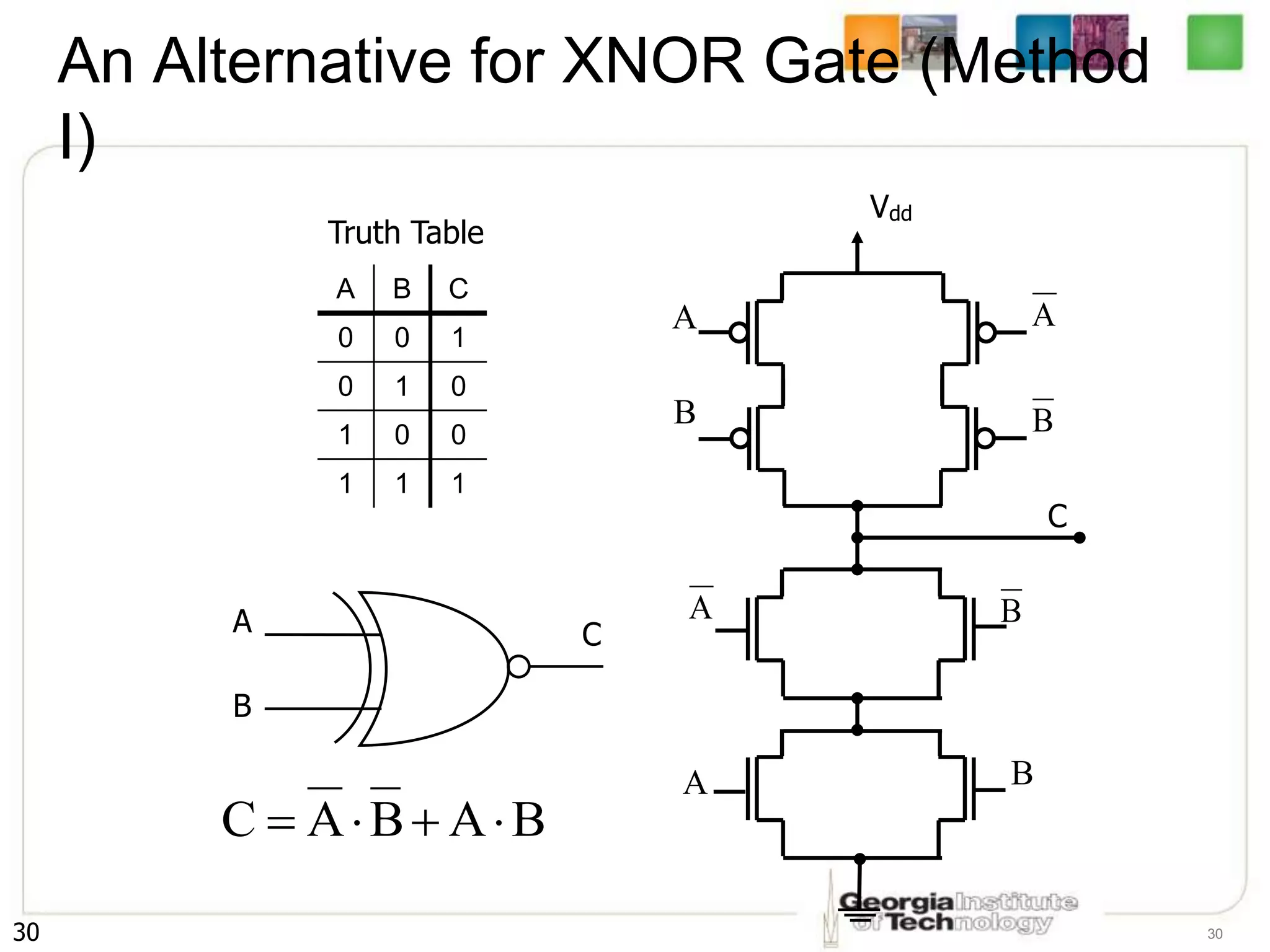
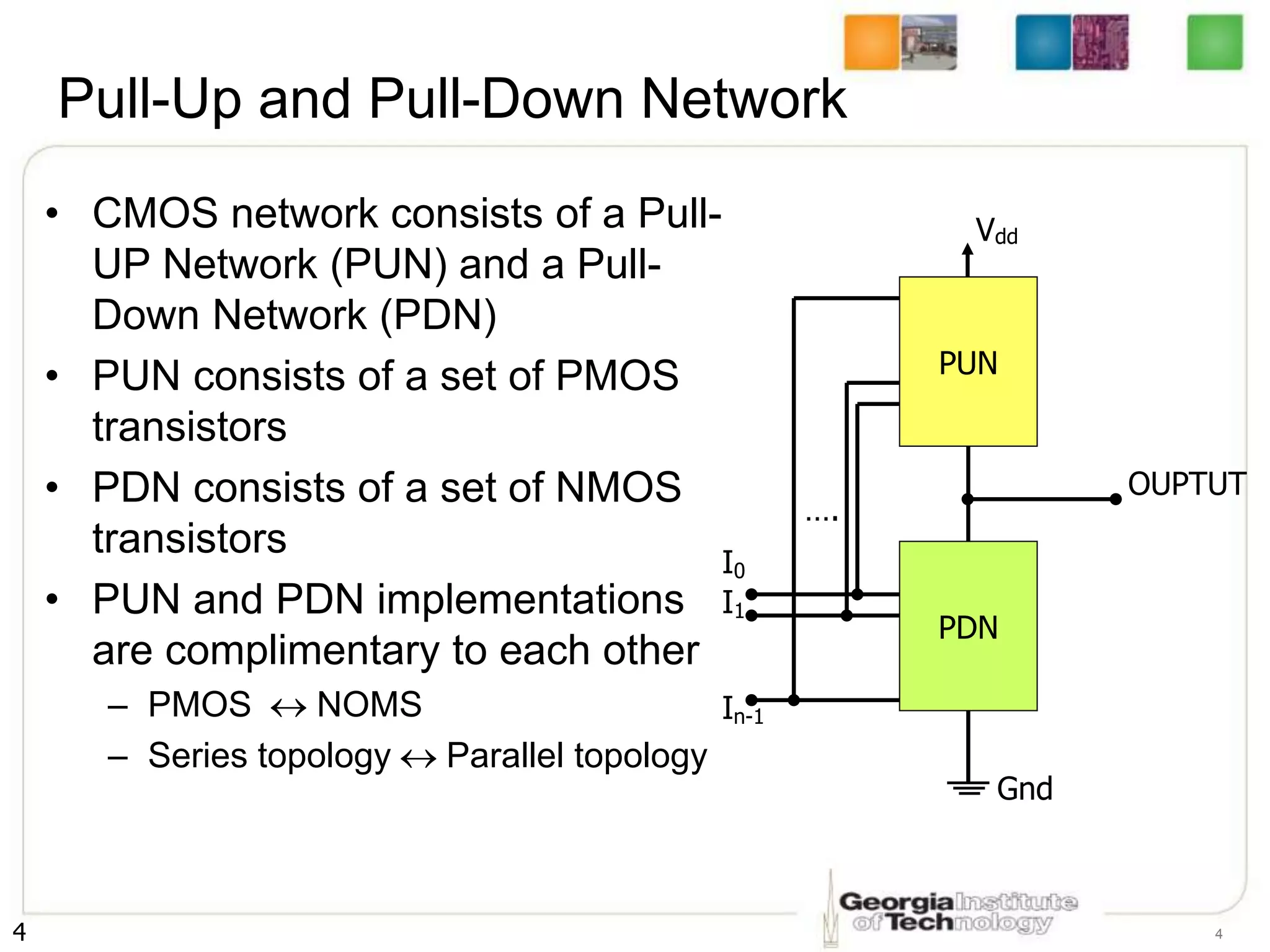
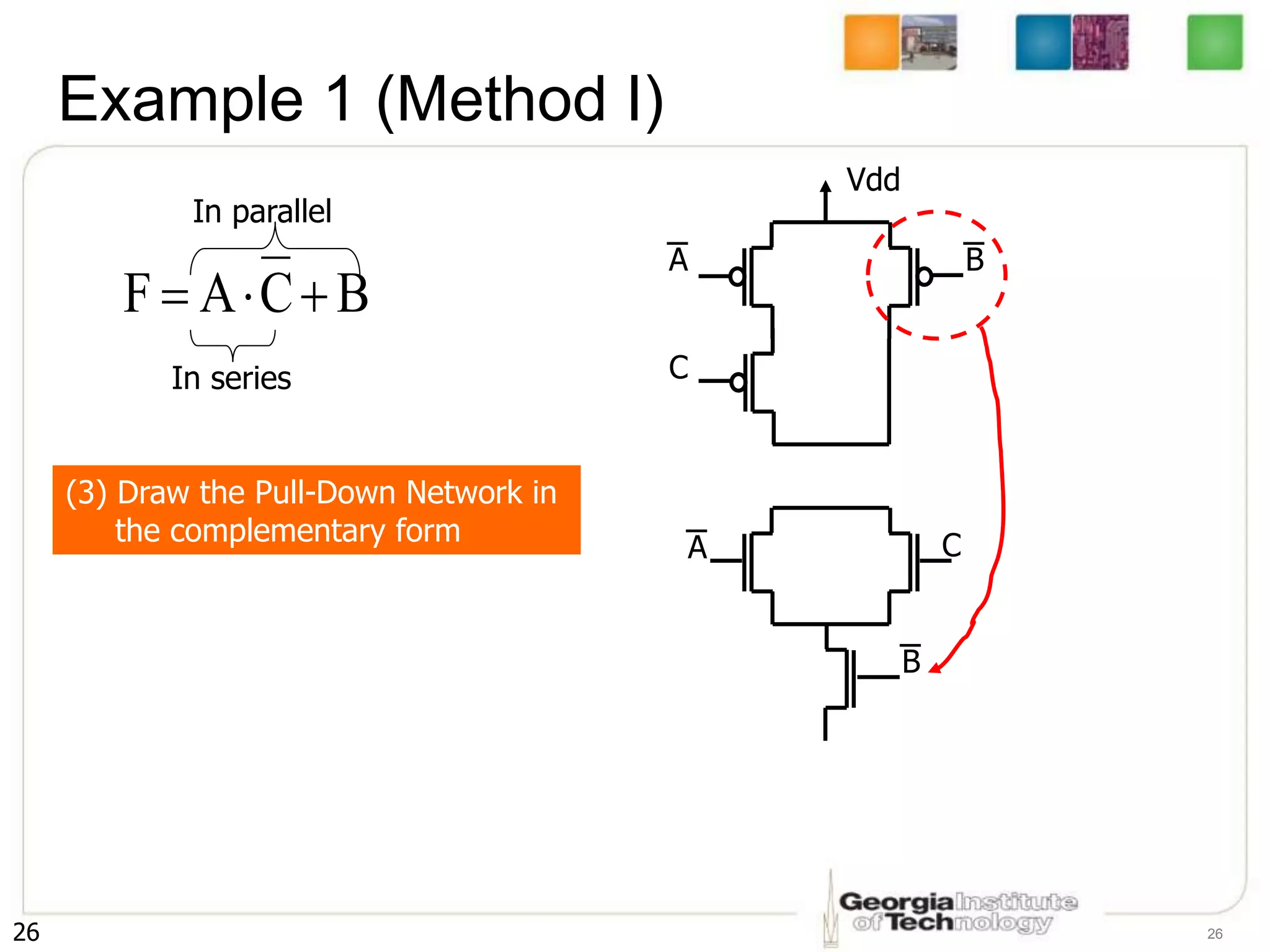
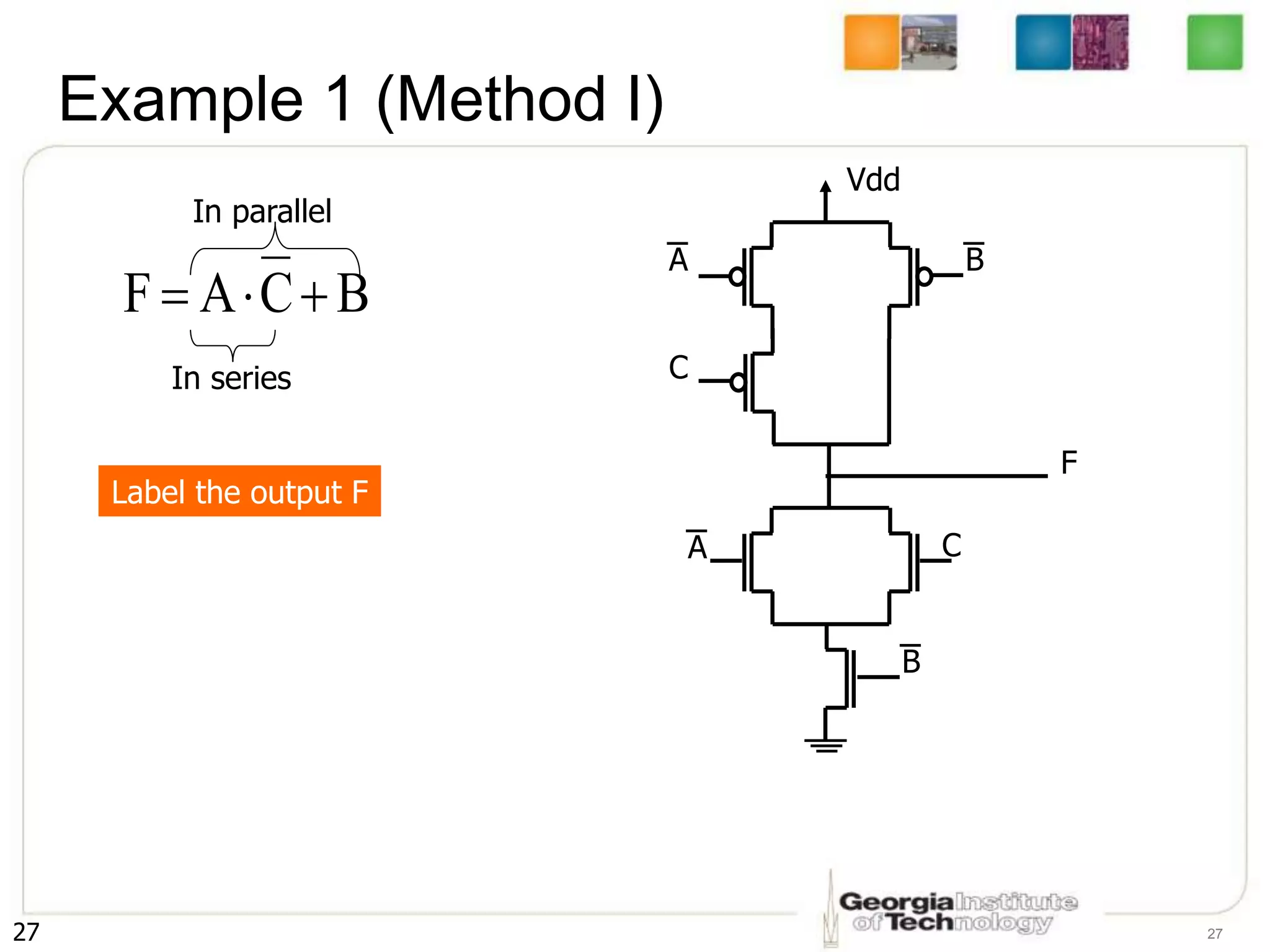
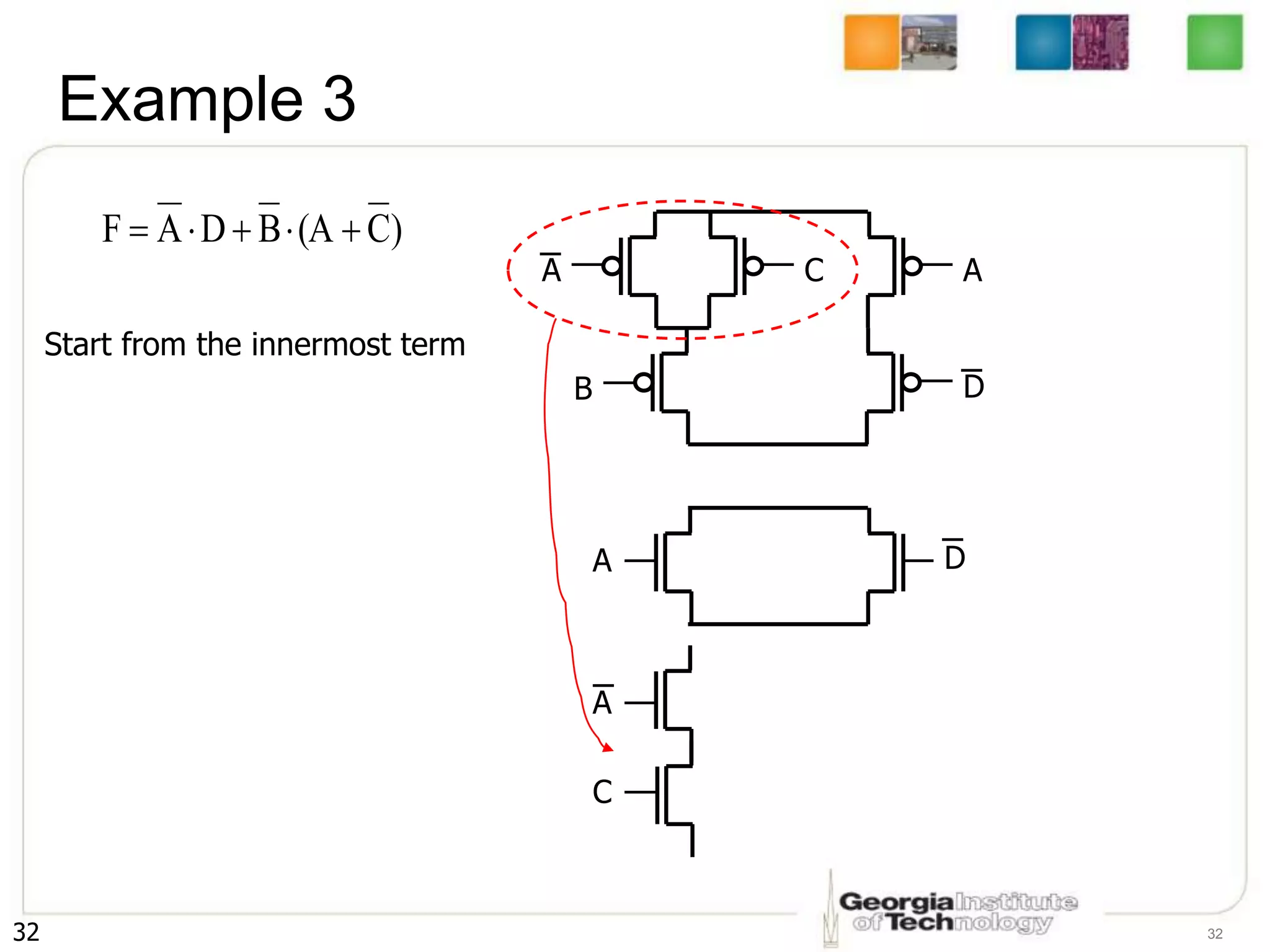
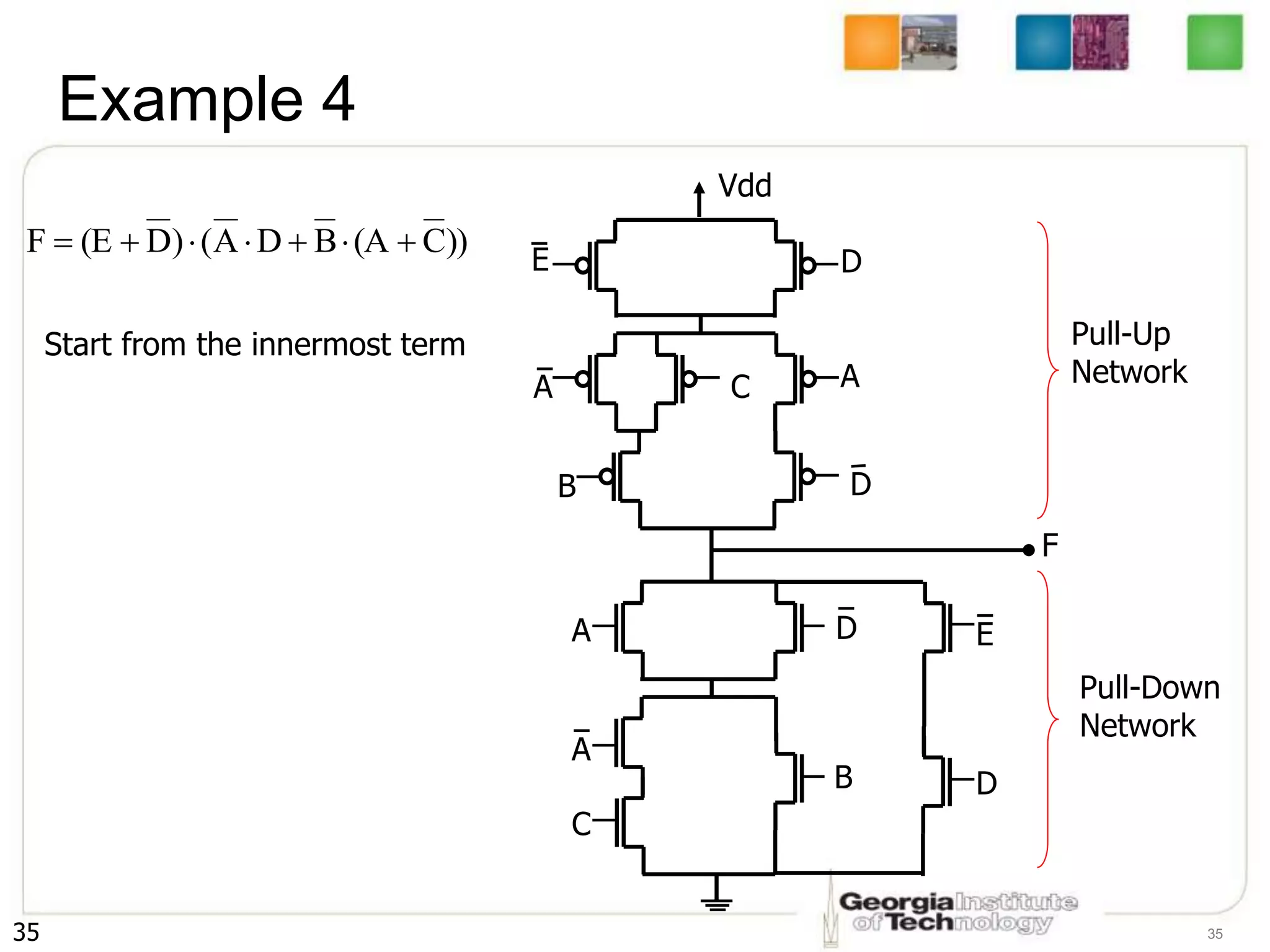
1. The document discusses CMOS inverters and basic gates like NAND and NOR. 2. It describes how to systematically design the pull-up network and pull-down network that make up a CMOS circuit from a Boolean equation. 3. The key steps are to represent each variable as a transistor, connect transistors in series for AND and parallel for OR, and ensure the pull-up and pull-down networks are complements of each other.

1. ECE2030
Introduction to Computer Engineering
Lecture 4: CMOS Network
Prof. Hsien-Hsin Sean Lee
School of Electrical and Computer Engineering
Georgia Tech

2. 2 2
CMOS Inverter
• Connect the following terminals of a PMOS and an
NMOS
– Gates
– Drains
Vin Vout
Vdd
Gnd
Vout
Vin
Vin
Vin = HIGH
Vout = LOW (Gnd)
ON
OFF
Vdd
Gnd
Vout
Vin
Vin
Vin = LOW
Vout = HIGH (Vdd)
ON
OFF
Vdd
PMOS
Ground
NMOS

3. 3 3
CMOS Voltage Transfer Characteristics
Vdd
Gnd
Vin Vout
PMOS
NMOS
OFF: V_GateToSource < V_Threshold
LINEAR (or OHMIC): 0< V_DrainToSource < V_GateToSource - V_Threshold
SATURATION: 0 < V_GateToSource - V_Threshold < V_DrainToSource
Note that in the CMOS Inverter  V_GateToSource = V_in

4. 4 4
Pull-Up and Pull-Down Network
• CMOS network consists of a Pull-
UP Network (PUN) and a Pull-
Down Network (PDN)
• PUN consists of a set of PMOS
transistors
• PDN consists of a set of NMOS
transistors
• PUN and PDN implementations
are complimentary to each other
– PMOS  NOMS
– Series topology Parallel topology
….
I0
I1
In-1
OUPTUT
Vdd
PUN
Gnd
PDN

5. 5 5
PUN/PDN of a CMOS Inverter
A B
0 1
1 Z
A B
0 Z
1 0
A B
0 1
1 0
Pull-Up
Network
Pull-Down
Network
Combined
CMOS
Network
Vdd
A
Gnd
B
CMOS Inverter

6. 6 6
Gate Symbol of a CMOS Inverter
Vdd
A
Gnd
B
CMOS Inverter
A B
B = Ā

7. 7 7
PUN/PDN of a NAND Gate
A B C
0 0 1
0 1 1
1 0 1
1 1 Z
A B C
0 0 Z
0 1 Z
1 0 Z
1 1 0
Pull-Up
Network
Pull-Down
Network
Vdd
A
B
A B
C

8. 8 8
PUN/PDN of a NAND Gate
A B C
0 0 1
0 1 1
1 0 1
1 1 Z
A B C
0 0 Z
0 1 Z
1 0 Z
1 1 0
A B C
0 0 1
0 1 1
1 0 1
1 1 0
Pull-Up
Network
Pull-Down
Network
Combined
CMOS
Network
Vdd
A
B
A B
C

9. 9 9
NAND Gate Symbol
A B C
0 0 1
0 1 1
1 0 1
1 1 0
Vdd
A
B
A B
C
A
B
C
Truth Table
B
A
C 


10. 10 10
PUN/PDN of a NOR Gate
A B C
0 0 1
0 1 Z
1 0 Z
1 1 Z
A B C
0 0 Z
0 1 0
1 0 0
1 1 0
Pull-Up
Network
Pull-Down
Network
Vdd
A
C
B
A B

11. 11 11
PUN/PDN of a NOR Gate
A B C
0 0 1
0 1 Z
1 0 Z
1 1 Z
A B C
0 0 Z
0 1 0
1 0 0
1 1 0
A B C
0 0 1
0 1 0
1 0 0
1 1 0
Pull-Up
Network
Pull-Down
Network
Combined
CMOS
Network
A
C
B
A B
Vdd

12. 12 12
NOR Gate Symbol
A B C
0 0 1
0 1 0
1 0 0
1 1 0
A
B
C
Truth Table
A
C
B
A B
B
A
C 

Vdd

13. 13 13
How about an AND gate
Vdd
A
B
A
Vdd
Gnd
C
NAND
Inverter
B
C = A B
A
B
C

14. 14 14
An OR Gate
A
B
A B
Vdd
Vdd
Gnd
C
Inverter
NOR
A
B
C
B
A
C 


15. 15 15
What’s the Function of the following CMOS Network?
A B C
0 0 Z
0 1 1
1 0 1
1 1 Z
A B C
0 0 0
0 1 Z
1 0 Z
1 1 0
A B C
0 0 0
0 1 1
1 0 1
1 1 0
Pull-Up
Network
Pull-Down
Network
Combined
CMOS
Network
Function = XOR
Vdd
A
B
A
A
A
B
B
B
C

16. 16 16
Yet Another XOR CMOS Network
Vdd
A
B
A A
A
B
B
B
C
A B C
0 0 Z
0 1 1
1 0 1
1 1 Z
A B C
0 0 0
0 1 Z
1 0 Z
1 1 0
A B C
0 0 0
0 1 1
1 0 1
1 1 0
Pull-Up
Network
Pull-Down
Network
Combined
CMOS
Network
Function = XOR

17. 17 17
Exclusive-OR (XOR) Gate
Vdd
A
B
A A
A
B
B
B
C
A B C
0 0 0
0 1 1
1 0 1
1 1 0
A
B
C
Truth Table
B
A
B
A
B
A
C 






18. 18 18
How about XNOR Gate
A B C
0 0 1
0 1 0
1 0 0
1 1 1
A
B
C
Truth Table
B
A
B
A
B
A
C 





How do we draw the
corresponding CMOS network
given a Boolean equation?

19. 19 19
How about XNOR Gate
A B C
0 0 1
0 1 0
1 0 0
1 1 1
A
B
C
Truth Table
B
A
B
A
C 



Vdd
A
B
A A
A
B
B
B
C
Vdd
XOR
Inverter

20. 20 20
A Systematic Method (I)
Start from Pull-Up Network
• Each variable in the given Boolean eqn
corresponds to a PMOS transistor in PUN and an
NMOS transistor in PDN
• Draw PUN using PMOS based on the Boolean eqn
– AND operation drawn in series
– OR operation drawn in parallel
• Invert each variable of the Boolean eqn as the gate
input for each PMOS in the PUN
• Draw PDN using NMOS in complementary form
– Parallel (PUN) to series (PDN)
– Series (PUN) to parallel (PDN)
• Label with the same inputs of PUN
• Label the output

21. 21 21
A Systematic Method (II)
Start from Pull-Down Network
• Each variable in the given Boolean eqn corresponds to a
PMOS transistor in PUN and an NMOS transistor in PDN
• Invert the Boolean eqn
• With the Right-Hand Side of the newly inverted equation,
Draw PDN using NMOS
– AND operation drawn in series
– OR operation drawn in parallel
• Label each variable of the Boolean eqn as the gate input for
each NMOS in the PDN
• Draw PUN using PMOS in complementary form
– Parallel (PUN) to series (PDN)
– Series (PUN) to parallel (PDN)
• Label with the same inputs of PUN
• Label the output

22. 22 22
Systematic Approaches
• Note that both methods lead to exactly the same
implementation of a CMOS network
• The reason to invert Output equation in (II) is
because
– Output (F) is conducting to “ground”, i.e. 0, when there
is a path formed by input NMOS transistors
– Inversion will force the desired result from the equation
• Example
– F=Ā·C + B: When (A=0 and C=1) or B=1, F=1.
However, in the PDN (NMOS) of a CMOS network,
F=0, i.e. an inverse result.
– Revisit how a NAND CMOS network is implemented
• Inverting each PMOS input in (I) follow the same
reasoning

23. 23 23
Example 1 (Method I)
B
C
A
F 


In series
In parallel
Vdd
(1) Draw the Pull-Up Network

24. 24 24
Example 1 (Method I)
B
C
A
F 


In series
In parallel
Vdd
(2) Assign the complemented input
A
C
B

25. 25 25
Example 1 (Method I)
B
C
A
F 


In series
In parallel
Vdd
(3) Draw the Pull-Down Network in
the complementary form
A
C
B
A C

26. 26 26
Example 1 (Method I)
B
C
A
F 


In series
In parallel
Vdd
(3) Draw the Pull-Down Network in
the complementary form
A
C
B
A C
B

27. 27 27
Example 1 (Method I)
B
C
A
F 


In series
In parallel
Vdd
Label the output F
A
C
B
A C
B
F

28. 28 28
Example 1 (Method I)
B
C
A
F 


In series
In parallel
Vdd
A
C
B
A C
B
F
A B C F
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1
Truth Table

29. 29 29
Drawing the Schematic using Method II
B
C
A
F 


B
C)
A
(
F
B
C
A
F
B
C
A
F









Vdd
A
C
B
A C
B
F
This is exactly the same
CMOS network with the
schematic by Method I

30. 30 30
An Alternative for XNOR Gate (Method
I)
A B C
0 0 1
0 1 0
1 0 0
1 1 1
A
B
C
Truth Table
B
A
B
A
C 



Vdd
A
B
A
B
A
A B
B
C

31. 31 31
Example 3
)
C
(A
B
D
A
F 




Start from the innermost term
A
B D
A
C
A D

32. 32 32
Example 3
)
C
(A
B
D
A
F 




Start from the innermost term
A
B D
A
C
A D
A
C

33. 33 33
Example 3
)
C
(A
B
D
A
F 




Start from the innermost term
A
B D
A
C
A D
A
C
B

34. 34 34
Example 3
)
C
(A
B
D
A
F 




Start from the innermost term
A
B D
A
C
A D
A
C
B
Vdd
F
Pull-Up
Network
Pull-Down
Network

35. 35 35
Example 4
))
C
(A
B
D
A
(
)
D
(E
F 






Start from the innermost term
A
B D
A
C
A D
A
C
B
Vdd
F
E D
E
D
Pull-Down
Network
Pull-Up
Network

36. 36 36
Another Example
B
C
A
F 

 How ??