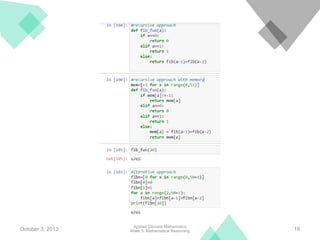
The document discusses recursive definitions, which define an object in terms of itself. It provides examples of recursively defined sequences, functions, and sets. Recursion is related to mathematical induction. Recursive algorithms solve problems by reducing them to smaller instances of the same problem. While recursive definitions and algorithms are elegant, iterative equivalents are typically more efficient in terms of time and space usage.