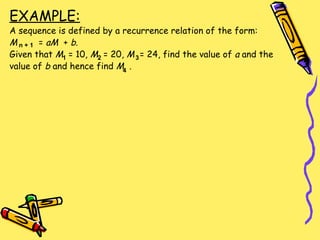
The document discusses sequences, which are sets of terms in a definite order obtained by some rule. It provides examples of finite and infinite sequences and discusses notation for representing sequences. It also covers finding the formula for the terms of a sequence using recurrence relations, which define the initial terms and the relationship between successive terms. The document gives examples of identifying patterns in sequences and finding subsequent terms.

2. SEQUENCES

3. A sequence is a set of terms, in a definite order, where the terms are obtained by some rule. A finite sequence ends after a certain number of terms. An infinite sequence is one that continues indefinitely.

4. For example: 1, 3, 5, 7, … (This is a sequence of odd numbers) 1st term = 2 x 1 – 1 = 1 2nd term = 2 x 2 – 1 = 3 3rd term = 2 x 3 – 1 = 5 nth term = 2 x n – 1 = 2 n - 1 . . . . . . + 2 + 2

5. NOTATION 1st term = u 2nd term = u 3rd term = u n th term = u . . . . . . 1 2 3 n

6. OR 1st term = u 2nd term = u 3rd term = u n th term = u . . . . . . 0 1 2 n-1

7. FINDING THE FORMULA FOR THE TERMS OF A SEQUENCE

8. A recurrence relation defines the first term(s) in the sequence and the relation between successive terms.

9. u = 5 u = u +3 = 8 u = u +3 = 11 u = u +3 = 3 n + 2 . . . 1 2 3 n+1 For example: 5, 8, 11, 14, … 1 2 n

10. What to look for when looking for the rule defining a sequence

11. Constant difference: coefficient of n is the difference 2 nd level difference: compare with square numbers ( n = 1, 4, 9, 16, …) 3 rd level difference: compare with cube numbers ( n = 1, 8, 27, 64, …) None of these helpful: look for powers of numbers (2 = 1, 2, 4, 8, …) Signs alternate: use (-1) and (-1) -1 when k is odd +1 when k is even k k 2 3 n - 1

12. EXAMPLE: Find the next three terms in the sequence 5, 8, 11, 14, …

13. EXAMPLE: The nth term of a sequence is given by x = Find the first four terms of the sequence. b) Which term in the sequence is ? c) Express the sequence as a recurrence relation. 1 __ 2 n n 1 1024 ____

14. EXAMPLE: Find the nth term of the sequence +1, -4, +9, -16, +25, …

15. EXAMPLE: A sequence is defined by a recurrence relation of the form: M = aM + b . Given that M = 10, M = 20, M = 24, find the value of a and the value of b and hence find M . n + 1 1 3 2 4