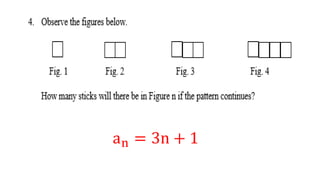
The given document discusses arithmetic sequences and their properties. It defines an arithmetic sequence as a sequence where each term is obtained by adding a fixed number (called the common difference) to the preceding term. It provides the formula for calculating the nth term of an arithmetic sequence as an = a1 + d(n - 1), where a1 is the first term and d is the common difference. Examples are provided to determine if a sequence is arithmetic or not based on this definition and formula. The document also contains practice problems asking users to find missing terms, identify patterns, and calculate specific terms of arithmetic sequences.

1. 3. Twice the sum a number and six is
twenty-four. What is the number?
2. A number minus seven yields ten.
Find the number.
1. Five more than a number is eight.
What is the number?
Drill: Solve each problem through mental calculation.
Explain your answer.

2. Evaluating Algebraic Expression
1. Evaluate 2𝑛 + 7 when 𝑛 = −4.
2. Evaluate 𝑚2
+ 4 when 𝑚 = 2.

3. SEQUENCE
Prepared by: Reno Lope

4. After going through this module, you are expected to
generate and describe patterns.
Objective:

5. Do you believe that our universe
is full of patterns? Why?

6. 1.What is the next number?
What is the 10th number?
0, 4, 8, 12, 16, ______
20
10th number: 36
The pattern is
adding 4 to the
previous value.

7. 2. What is the next number?
What is the 8th number?
9, 4, -1, -6, -11, ______
-16
8th number: -26
The pattern is
adding -5 to the
previous value.

8. 3. What is the next number?
What is the 12th number?
1, 3, 9, 27, 81, ______
243
12th number: 177, 147
The pattern is
multiplying 3 to the
previous value.

9. 4. What is the next number?
What is the 7th number?
160, 80, 40, 20, 10, _____
5
7th number:
5
2
The pattern is
dividing 2 or
multiplying
1
2
to
the previous
value.

10. 5. Observe the number of squares on each figure
below. How many squares will there be in the next
Figure? In Figure 8?
Figure 4: 9 squares
Figure 8: 17 squares
The pattern is
adding 2 squares
to the item.

11. State the pattern.

12. A Sequence is an ordered
list of values/objects which
follows a definite pattern.

14. After going through this lesson, you are expected to:
1. find the first five terms of a sequence given its nth
term.
Objectives:

15. A Sequence is an ordered
list of values/objects which
follows a definite pattern.

16. Each value in a sequence is called a term
with 𝒂𝟏 the first term, 𝒂𝟐 the second term,
and 𝑎𝑛 the nth term.

18. A sequence is either finite or infinite.
A finite sequence has a first term and last term.
Example: 3, 9, 15, 21, 27
An infinite sequence has first term but has no last term.
Example: 26, 19, 12, 5, -2, …
The sequence has 5 terms. The first
term 𝑎1 is 3. The last term which
the fifth term 𝑎5 is 27.
The sequence has endless terms. The
first term 𝑎1 is 26. The three dots
means that the sequence continues
forever.

19. The expression 𝒂𝒏 , which defines the
sequence, is called the general term of the
sequence.
Note: The general term of a sequence is the equation
or function that describe the sequence.
Function is an expression, rule, or law that defines a
relationship between one variable (the independent variable)
and another variable (the dependent variable).

20. (a) Calculate the first five terms
of the sequence described by the
formula 𝑎𝑛 = 2𝑛 + 3.
𝑎𝑛 = 2𝑛 + 3
n=1
𝑎1 = 2 1 + 3 = 5
n=2
𝑎2 = 2 2 + 3 = 7
n=3
𝑎3 = 2 3 + 3 = 9
n=4
𝑎4 = 2(4) + 3=11
n=5
𝑎5 = 2 5 + 3 = 13
The sequence is 5, 7, 9, 11, 13.
(b) What is the difference between the
terms of the sequence?
5, 7, 9, 11, 13
2 2 2 2
The difference between the terms of
the sequence is 2.
(c) Explain where does the difference
between the terms appears in the formula?
Formula: 𝑎𝑛 = 2𝑛 + 3
The difference between the terms appears as
the numerical coefficient of the variable n.

21. 2. Find the first five terms of the sequence
describes by the function 𝑎𝑛 = −3 𝑛
.
Domain: 1,2,3,4,5
n=1 𝑎1 = −3 1
= −3
n=2 𝑎𝑛 = −3 2
= 9
n=3 𝑎𝑛 = −3 3
= −27
n=4 𝑎𝑛 = −3 4
= 81
n=5 𝑎𝑛 = −3 5
= −243
𝑇ℎ𝑒 𝑠𝑒𝑞𝑢𝑒𝑛𝑐𝑒 𝑖𝑠
− 3, 9, −27, 81, −243

22. Group Activity: notebook
1. A sequence is defined by the formula .
(a) Calculate the first 5 terms of the sequence.
(b) What is the difference between the terms of the sequence?
2. A sequence is defined by the formula .
(a) Calculate the first 5 terms of the sequence.
(b) What is the difference between the terms of the sequence?
(c) Explain where the difference appears in the formula for the terms.
3. A sequence is defined by the formula .
(a) Calculate the first 5 terms of the sequence.
(b) What is the difference between terms for the sequence?
(c) How does this difference relate to the formula?
(d) Calculate the 20th term of the sequence.
an = 6n − 2
an = 8n + 2
an = 82 − 4n

23. Quiz: notebook
1. Calculate the 100th term of the sequence given by .
2. Calculate the 25th term of the sequence given by .
3. Calculate the 200th term of the sequence given by .
4. Calculate the 58th term of the sequence defined by .
an = 8n − 5
an = 11n − 3
an = 3n + 22
an = 1000 − 5n

24. After going through this lesson, you are expected to:
1. write the general or nth term of a sequence.
Objectives:

25. What is the general or nth term for each sequence?
1. 3,7,11,15,19,…
2. 4,1,-2,-5,…
3.
1
11
,
1
15
,
1
19
,
1
23
, …
an = 4n − 1
an = −3n + 7
an =
1
4n + 7
The pattern is adding the previous term by 4.
The first term is one less than the difference of the two successive
terms of the sequence.
The pattern is adding the previous term by – 3. The first term is
seven more that the difference of the two successive terms of the
sequence.
The pattern is the denominator of each term of
the sequence is increased by 4.
Note: To generate patterns, you
should be observant. Make sure
that you check all the terms in the
sequence before deciding what the
pattern is.

26. an = 3n + 1

27. In Bangkal High School, suspension of classes
is announced through text brigade. One stormy
day, the principal announces the suspension of
classes to two teachers, each of whom send this
message to two other teachers, and so on. How
many text messages were sent after n rounds?
an = 2n

28. Seatwork:
Write the nth term for each sequence below.
1. 2, 5, 8, 11, 14, …
2. 1, 2, 4, 8, 16, 32, …
3. 1,
1
2
,
1
3
,
1
4
,
1
5

29. 1. Find the missing term in the following sequence: 8, __, 16, __, 24,
28, 32.
2. What is the value of n in the following number sequence?
16, 21, n, 31, 36
3. It is an ordered list of numbers (or other elements like geometric
objects) that often follows a specific pattern or function.
4. What is the nth term of the sequence 7, 9, 11, 13, 15, 17…?
5. What is the 10th term of the sequence whose nth term is 𝑎𝑛 =
𝑛2−1
𝑛2+1
?
Answer each question. Write your answer/solution below each number.

30. 6. Find the missing terms in the following sequence:
12, 17, 22, 27, 32, ___, ___
7. What is the value of n in the following number sequence?
5, 15, 45, n, 405
8. What is the nth term of the sequence 7, 11, 15, 19, 23, 27, . . . ?
9. What is the next two terms of the sequence
1
11
,
1
15
,
1
19
,
1
23
, …?
10. What is the nth term of the sequence
1
2
,
1
4
,
1
6
,
1
8
, … ?

31. Arithmetic Sequence

32. An Arithmetic sequence is a sequence of numbers in
which each term after the first is obtained by adding a
fixed number called common difference, d, to the
preceding term. The nth term of an arithmetic
sequence is defined as
𝒂𝒏 = 𝒂𝟏 + 𝒅(𝒏 − 𝟏)
where 𝑎1 = the first term
𝑎𝑛 = the nth term
d = the common difference

33. Determine whether each of the sequences is
Arithmetic or not. If it is, find the common difference
d and the next 2 terms.
1.3, 10, 17, 24, …
2. 9.5, 7.5, 5.5, 3.5, …
3. 12
, 22
, 32
, 42
, 52
, 62
, 72
, …
4. 3, -6, 12, -24, …
Arithmetic, d=7, 31 and 38
Arithmetic, d= - 2, 1.5 and -0.5
Not Arithmetic
Not Arithmetic

34. 5. 1,
1
2
, 0, −
1
2
, …
6. 1, 2, 3, 4, 5, 8, …
7.
1
2
,
1
3
,
1
4
,
1
5
…
8. 20, 15, 10, 5, 0, -5, -10, …
Arithmetic, d= −
1
2
, −1𝑎𝑛𝑑 −
3
2
Not Arithmetic
Not Arithmetic
Arithmetic, d= - 5, -15 and -20

35. What is the fifth term of an arithmetic sequence if the first
term is 3 and the common difference is 7? Use the formula
𝒂𝒏 = 𝒂𝟏 + 𝒅(𝒏 − 𝟏).
Solution:
Given: 𝑎1 = 3 𝑑 = 7 𝑎5 =?
𝑎𝑛 = 𝑎1 + 𝑑(𝑛 − 1) Formula
𝑎5 = 3 + 7(5 − 1) Substitute n by 5, 𝑎1 by 3 and d by 7.
𝑎5 = 3 + 7(4) Simplify
𝑎5 = 3 + 28
𝑎5 = 31
The fifth term of the arithmetic sequence is 31.