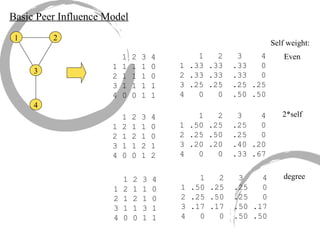
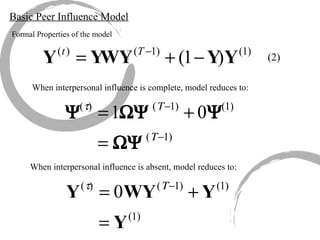
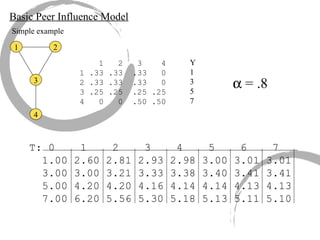
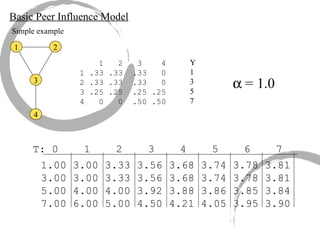
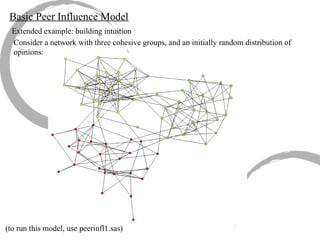
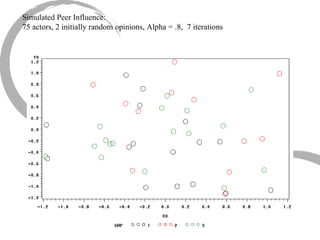
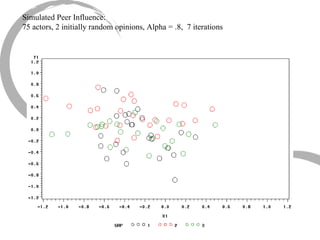
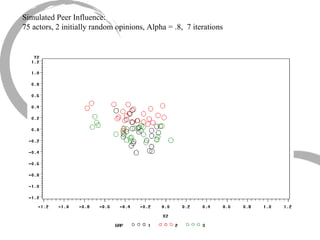
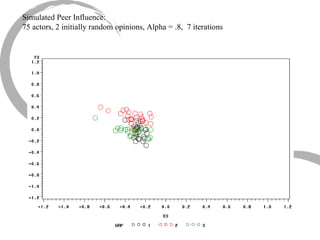
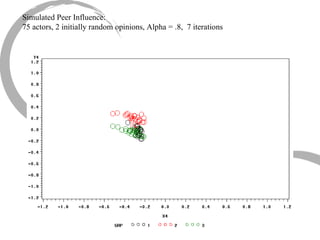
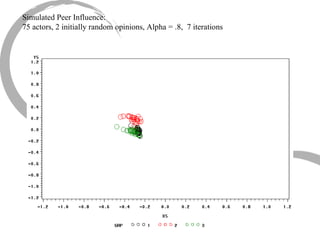
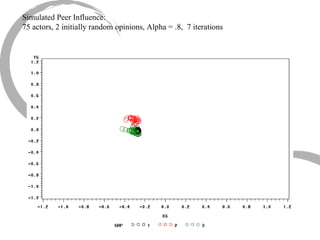
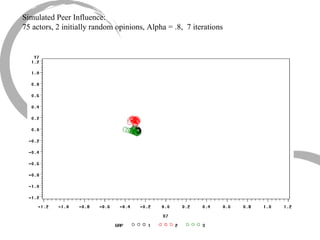
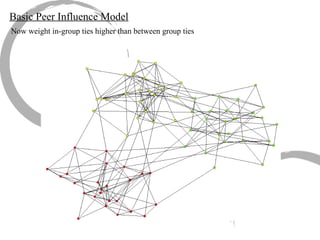
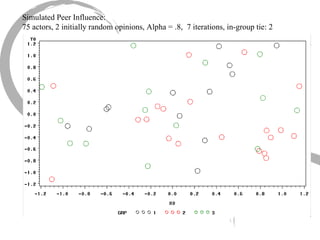
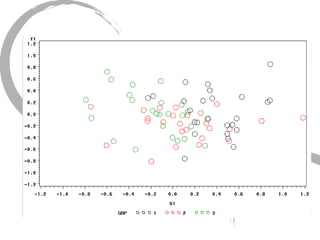
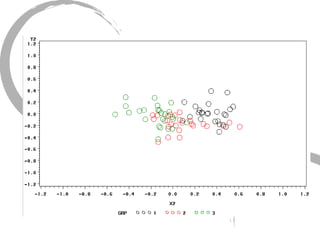
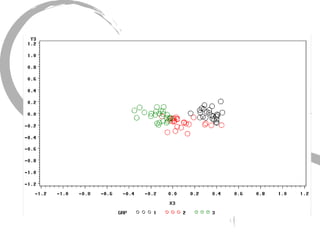
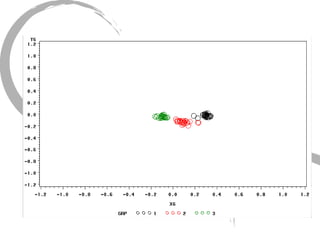
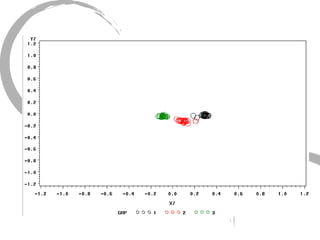
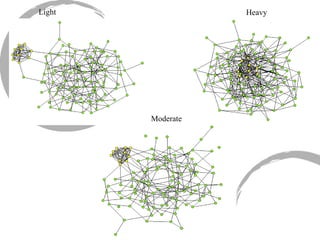
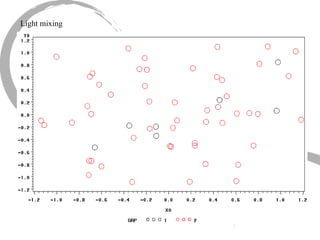
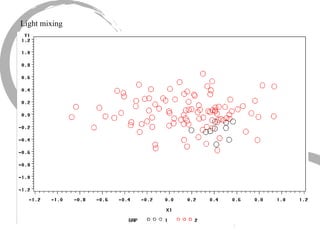
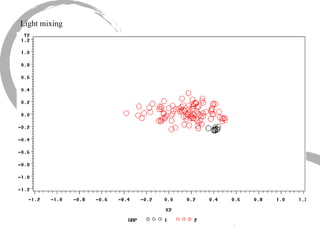
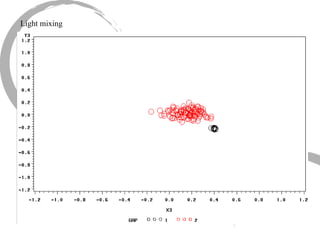
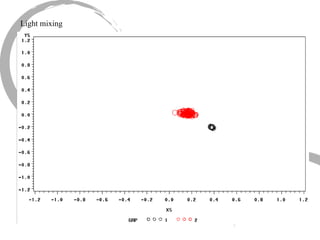
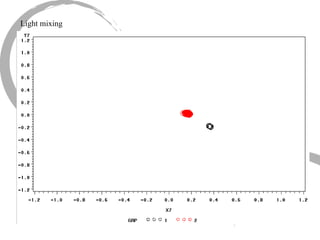
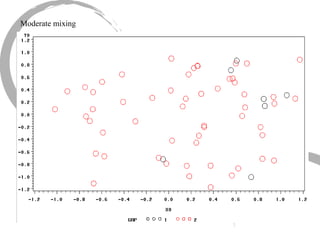
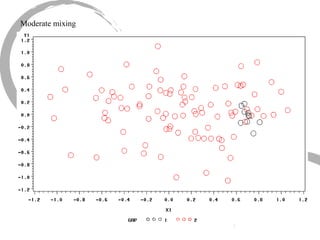
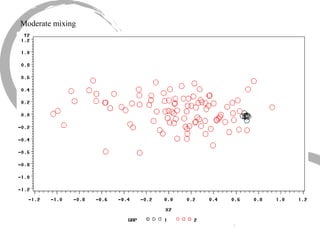
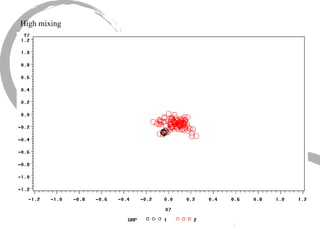
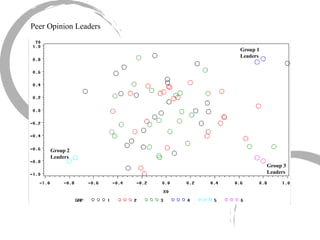
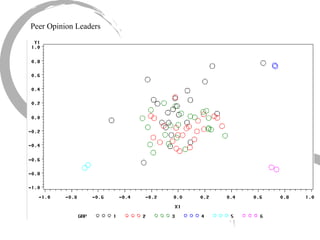
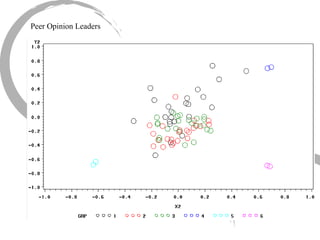
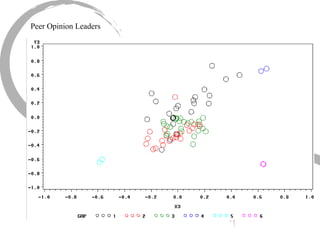
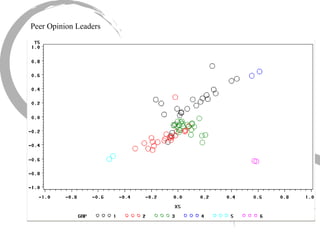
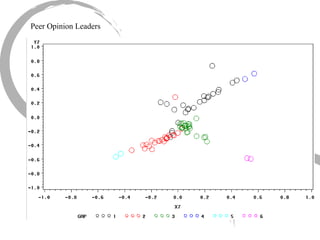
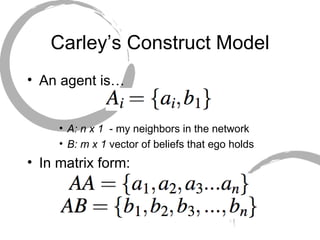
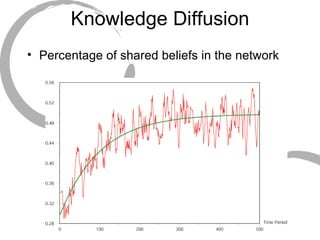
The document discusses how social networks and individual attitudes influence each other through two related processes: social contagion and homophily. Social contagion refers to the diffusion of attributes through a social network based on its structure, while homophily refers to the formation of social networks based on shared attributes among individuals. The document outlines Friedkin's model of social influence, which models how individuals' opinions are shaped both by their own characteristics and by interpersonal influences within their social network over multiple time periods.

1. How Networks Shape Attitudes and Attitudes Shape Networks Diffusion and Contagion

2. GridWorlds

3. Net Worlds

4. Contagion and Diffusion We choose our friends, and our friends choose us We learn from them, they learn from us Thus… Formation of networks and formation of attitudes are inextricably linked

5. Cont… We shall observe two processes that shape dynamic networks: Social contagion = diffusion of attributes shaped by network structure Formation of homophily groups = network structure shaped by attributes

6. Friedkin Contagion Model Peer influence models assume that individuals’ opinions are formed in a process of interpersonal negotiation and adjustment of opinions. Can result in either consensus or disagreement Looks at interaction among a system of actors Assumption that a network is static, but individuals change

7. Basic Peer Influence Model Attitudes are a function of two sources: a) Individual characteristics Gender, Age, Race, Education, Etc. Standard sociology b) Interpersonal influences Actors negotiate opinions with others

8. Freidkin claims in his Structural Theory of Social Influence that the theory has four benefits: Relaxes the simplifying assumption of actors who must either conform or deviate from a fixed consensus of others (public choice model) Does not necessarily result in consensus, but can have a stable pattern of disagreement Is a multi-level theory: micro level: cognitive theory about how people weigh and combine other’s opinions macro level: concerned with how social structural arrangements enter into and constrain the opinion-formation process Allows an analysis of the systemic consequences of social structures Basic Peer Influence Model

9. Influenfce Model in English Every agents’ beliefs are affected by the beliefs of agents he is connected to At time t+1 Ego belief= weight *Ego belief at time t + Sum( weight * belief of alter) For all alters connected to ego

10. The same, in Matrix Form (1) (2) Y (1) = an N x M matrix of initial opinions on M issues for N actors X = an N x K matrix of K exogenous variable that affect Y B = a K x M matrix of coefficients relating X to Y  = a weight of the strength of endogenous interpersonal influences (how much is ego influenced by alters) W = an N x N matrix of interpersonal influences

11. Basic Peer Influence Model Formal Model (1) This is the standard sociology model for explaining anything: the General Linear Model. It says that a dependent variable (Y) is some function (B) of a set of independent variables (X). At the individual level, the model says that: Usually, one of the X variables is  , the model error term.

12. Basic Peer Influence Model (2) This part of the model taps social influence. It says that each person’s final opinion is a weighted average of their own initial opinions And the opinions of those they communicate with (which can include their own current opinions)

13. Basic Peer Influence Model The key to the peer influence part of the model is W , a matrix of interpersonal weights. W is a function of the communication structure of the network, and is usually a transformation of the adjacency matrix. In general: Various specifications of the model change the value of w ii , the extent to which one weighs their own current opinion and the relative weight of alters.

14. Basic Peer Influence Model 1 2 3 4 1 2 3 4 1 1 1 1 0 2 1 1 1 0 3 1 1 1 1 4 0 0 1 1 1 2 3 4 1 .33 .33 .33 0 2 .33 .33 .33 0 3 .25 .25 .25 .25 4 0 0 .50 .50 1 2 3 4 1 .50 .25 .25 0 2 .25 .50 .25 0 3 .20 .20 .40 .20 4 0 0 .33 .67 Even 2*self 1 2 3 4 1 .50 .25 .25 0 2 .25 .50 .25 0 3 .17 .17 .50 .17 4 0 0 .50 .50 degree Self weight: 1 2 3 4 1 2 1 1 0 2 1 2 1 0 3 1 1 2 1 4 0 0 1 2 1 2 3 4 1 2 1 1 0 2 1 2 1 0 3 1 1 3 1 4 0 0 1 1

15. Basic Peer Influence Model Formal Properties of the model When interpersonal influence is complete, model reduces to: When interpersonal influence is absent, model reduces to: (2)

16. Basic Peer Influence Model Simple example 1 2 3 4 1 2 3 4 1 .33 .33 .33 0 2 .33 .33 .33 0 3 .25 .25 .25 .25 4 0 0 .50 .50 Y 1 3 5 7  = .8 T: 0 1 2 3 4 5 6 7 1.00 2.60 2.81 2.93 2.98 3.00 3.01 3.01 3.00 3.00 3.21 3.33 3.38 3.40 3.41 3.41 5.00 4.20 4.20 4.16 4.14 4.14 4.13 4.13 7.00 6.20 5.56 5.30 5.18 5.13 5.11 5.10

17. Basic Peer Influence Model Simple example 1 2 3 4 1 2 3 4 1 .33 .33 .33 0 2 .33 .33 .33 0 3 .25 .25 .25 .25 4 0 0 .50 .50 Y 1 3 5 7  = 1.0 1.00 3.00 3.33 3.56 3.68 3.74 3.78 3.81 3.00 3.00 3.33 3.56 3.68 3.74 3.78 3.81 5.00 4.00 4.00 3.92 3.88 3.86 3.85 3.84 7.00 6.00 5.00 4.50 4.21 4.05 3.95 3.90 T: 0 1 2 3 4 5 6 7

18. Basic Peer Influence Model Extended example: building intuition Consider a network with three cohesive groups, and an initially random distribution of opinions: (to run this model, use peerinfl1.sas)

19. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

20. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

21. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

22. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

23. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

24. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

25. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

26. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations

27. Basic Peer Influence Model Now weight in-group ties higher than between group ties

28. Simulated Peer Influence: 75 actors, 2 initially random opinions, Alpha = .8, 7 iterations, in-group tie: 2

34. Consider the implications for populations of different structures. For example, we might have two groups, a large orthodox population and a small heterodox population. We can imagine the groups mixing in various levels: Heterodox: 10 people Orthodox: 100 People

35. Light Heavy Moderate

36. Light mixing

37. Light mixing

38. Light mixing

39. Light mixing

40. Light mixing

41. Light mixing

42. Moderate mixing

43. Moderate mixing

44. Moderate mixing

45. Moderate mixing

46. Moderate mixing

47. Moderate mixing

48. High mixing

49. High mixing

50. High mixing

51. High mixing

52. High mixing

53. High mixing

54. Size Matters In an unbalanced situation (small group vs large group) the extent of contact can easily overwhelm the small group. Applications of this idea are evident in: Missionary work (Must be certain to send missionaries out into the world with strong in-group contacts) Overcoming deviant culture (I.e. youth gangs vs. adults)

55. Factoring in Trust In recent extensions (Friedkin, 1998), Friedkin generalizes the model so that alpha varies across people. We can extend the basic model by (1) simply changing  to a vector ( A ), which then changes each person’s opinion directly, and (2) by linking the self weight (w ii ) to alpha. Were A is a diagonal matrix of endogenous weights, with 0 < a ii < 1. A further restriction on the model sets w ii = 1-a ii This leads to a great deal more flexibility in the theory, and some interesting insights. Consider the case of group opinion leaders with unchanging opinions (I.e. many people have high a ii , while a few have low):

56. Group 1 Leaders Group 2 Leaders Group 3 Leaders Peer Opinion Leaders

57. Peer Opinion Leaders

58. Peer Opinion Leaders

59. Peer Opinion Leaders

60. Peer Opinion Leaders

61. Peer Opinion Leaders

62. Extensions of the Model Time dependent  : people likely value other’s opinions more early than later in a decision context Can be done in context of simulated annealing; Randomization in  Interact  with XB: people’s self weights are a function of their behaviors & attributes

63. Make W dependent on structure of the network (weight transitive ties greater than intransitive ties, for example) Time dependent W : The network of contacts does not remain constant, but is dynamic, meaning that influence likely moves unevenly through the network Extensions of the Model

64. Friedkin & Cook One piece in a long standing research program. Other cites include: Friedkin, N. E. 1984. &quot;Structural Cohesion and Equivalence Explanations of Social Homogeneity.&quot; Sociological Methods and Research 12:235-61. ——— . 1998. A Structural Theory of Social Influence . Cambridge: Cambridge. Friedkin, N. E. and E. C. Johnsen. 1990. &quot;Social Influence and Opinions.&quot; Journal of Mathematical Sociology 15(193-205). ——— . 1997. &quot;Social Positions in Influence Networks.&quot; Social Networks 19:209-22.

65. So we know… … Attitudes and knowledge are affected by the network structure But is the network affected by the attitudes?

66. Carley’s Construct Model An agent is… A: n x 1 - my neighbors in the network B: m x 1 vector of beliefs that ego holds In matrix form:

67. Knowledge Network …or any 2-mode network “People x Attribute” “People x Resource” “People x Organization” …etc

68. How networks form Agents tend to communicated with either: People similar to them (I.e. with similar observed beliefs or attributes) Or People that can provide useful information

69. Need for Communicative Ease Relative similarity RS ij = how much I shares with J divided by how much I shares with all others B ik is belief network ( i knows information k ) Expected interaction based on relative similarity “ A ratio of what ego shares with alter to what ego shares with everybody else”

70. Need to Know Relative expertise RE ij = how much I thinks J knows that I does not know divided by how much I thinks all others know that I does not know S ik is knowledge network I knows information k Expected interaction based on relative expertise

71. What do we get from this… RS and RE are equivalent to probability of interaction At each time, agents get a chance to interact based on the probabilities An interaction=creation of a network tie Ties decay with time if not reactivated

72. Structural Evolution

73. Knowledge Diffusion Percentage of shared beliefs in the network

74. Summary Friedkin’s Contagion Model derives belief structures from network structures Carley’s Construct Model derives network structures from belief structures Construct allows simultaneous manipulation of beliefs and network structure