This document outlines a short course on opinion dynamics in networks, focusing on various models such as threshold models, adaptive voter models, and bounded-confidence models. It discusses how these models can explain the spread of opinions and misinformation in social networks while considering the impact of network structure on dynamics. The text highlights key studies, examples, and potential future research directions in the field.

1. Opinion Dynamics on Networks
Mason A. Porter (@masonporter)
Department of Mathematics, UCLA

3. Talks, Tutorials, Panels, and Slides from
our Short Course
•https://zerodivzero.com/short_course/aaac8c66007a4d23a7aa14857a3b778
c/titles

4. Spread of “Fake News” on Social Networks

5. Outline
• Introduction
• Threshold models
• Adaptive voter models
• Bounded-confidence models
• Conclusions

6. Introduction

7. Social Networks
• Typically (but not always), nodes represent individuals
• Depending on the application, edges can represent one (or more) of various types
of social connections: offline interactions, phone calls, Facebook ‘friendships’,
Twitter followership, etc.
• Notions of actual social ties, but also notions of communication
• Different things propagate on different types of networks
• For example: information spreading versus disease spreading
• Complicated mixture of regular and ‘random’ structures
• Good random-graph models provide baselines for comparison

8. Dynamical Processes on Networks
•Incorporate which individuals (nodes) interact with which other
individuals via their ties (edges).
•This yields a dynamical system on a network.
•Basic question: How does network structure affect dynamics (and
vice versa)?
•MAP & J. P Gleeson [2016], “Dynamical Systems on Networks: A
Tutorial”, Frontiers in Applied Dynamical Systems: Reviews and
Tutorials, Vol. 4

9. A General Note About Time Scales and Modeling
Dynamical Systems on Dynamical Networks
• Relative time scales of evolution of states versus evolution of network structure
• States change much faster than structure?
• Faster: Dynamical systems on static networks (“quenched”)
• MUCH faster (too rapidly): Can only trust statistical properties of states
• Structure changes much faster than states?
• Faster: Temporal networks
• MUCH faster (too rapidly): Can only trust statistical properties of network structure (“annealed”)
• Comparable time scales?
• “Adaptive” networks (aka “coevolving” networks)
• Dynamics of states of network nodes (or edges) coupled to dynamics of network structure

10. Spreading and Opinion Models
•There are many types of models, and the goal of my talk is to introduce
three types of them.
• Threshold models
• A type of model with discrete states (usually two of them) that models social
reinforcement in contagious spreading processes in a minimalist way
• Voter models
• Discrete-valued opinions, although not really a model for “voters”
• Bounded-confidence models
• Continuous-valued opinions

11. Threshold Models
Example: Watts Threshold Model
• D. J.Watts, PNAS, 2002
• Each node j has a (frozen) threshold Rj drawn from some distribution and can be in one of two states (0 or 1)
• Choose a seed fraction ρ(0) of nodes (e.g. uniformly at random) to initially be in state 1 (“infected”,“active”,
etc.)
• Updating can be either:
• Synchronous: discrete time; update all nodes at once
• Asynchronous:“continuous” time; update some fraction of nodes in time step dt (e.g., using a Gillespie
algorithm)
• Update rule: Compare fraction of infected neighbors (m/kj) to Rj. Node j becomes infected if m/kj ≥ Rj.
Otherwise no change.
• Variant (Centola–Macy): Look at number of active neighbors (m) rather than fraction of active neighbors
• Monotonicity: Nodes in state 1 stay there forever.
J. P. Gleeson, PRX,Vol. 3, 021004 (2013): has a table of more than 20 binary-state models (WTM, percolation models, etc.)

12. Steady-State Levels of Adoption

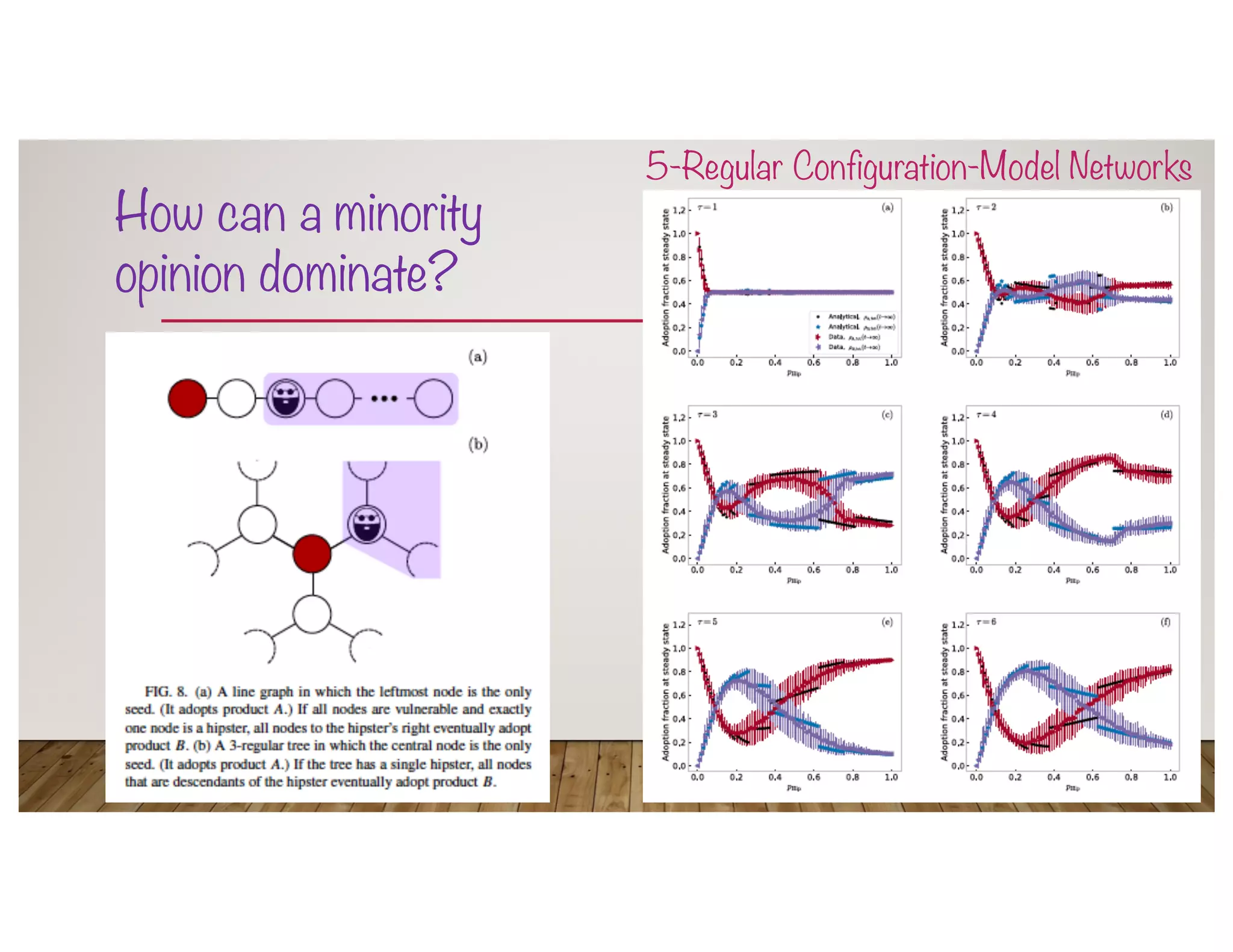
13. A Threshold Model with Hipsters
• J. S. Juul & MAP [2019], “ Hipsters on Networks: How a Minority Group of Individuals Can Lead to an
Antiestablishment Majority”, Physical Review E, Vol. 99: 022313
• WTM rules to adopt some product (A or B)
• Conformist node: Adopts majority opinion from local neighborhood
• Hipster node: Adopts minority opinion (from full network, like a best-seller list) from ! times ago

14. 5-Regular Configuration-Model Networks
How can a minority
opinion dominate?

15. Adaptive Voter Models

16. “The” Voter Model
• S. Redner [2019], “Reality Inspired Voter Models: A Mini-Review”, Comptes
Rendus Physique, Vol. 20:275–292
• In an update step, an individual updates their opinion based on the opinion of a
neighbor
• One choice: asynchronous versus synchronous updating
• Select a random node (e.g., uniformly at random) and then a random neighbor
• Another choice: node-based models versus edge-based models
• Select a random edge (or perhaps a random “discordant” edge)
• In Kureh & Porter (2020), we use asynchronous, edge-based updates.

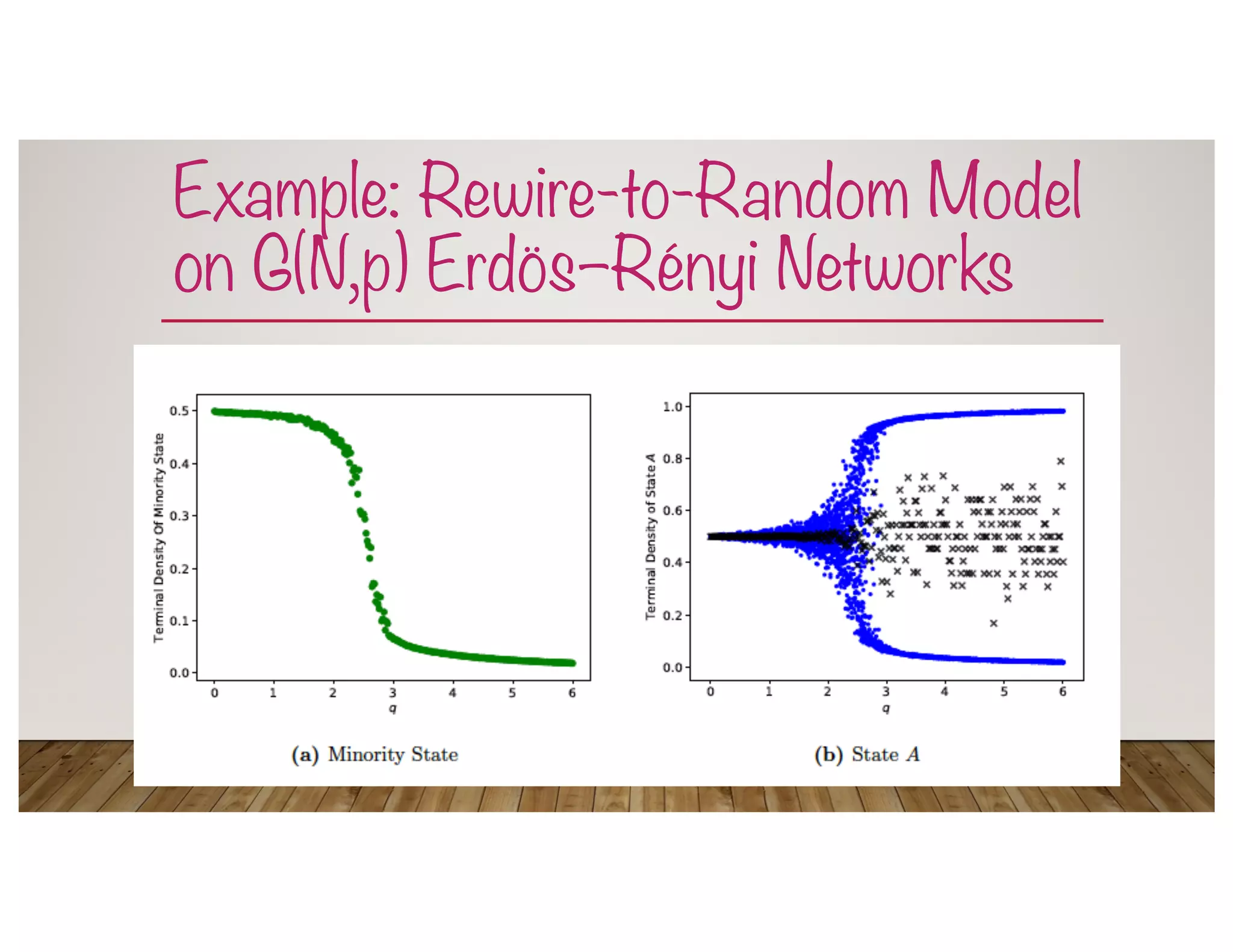
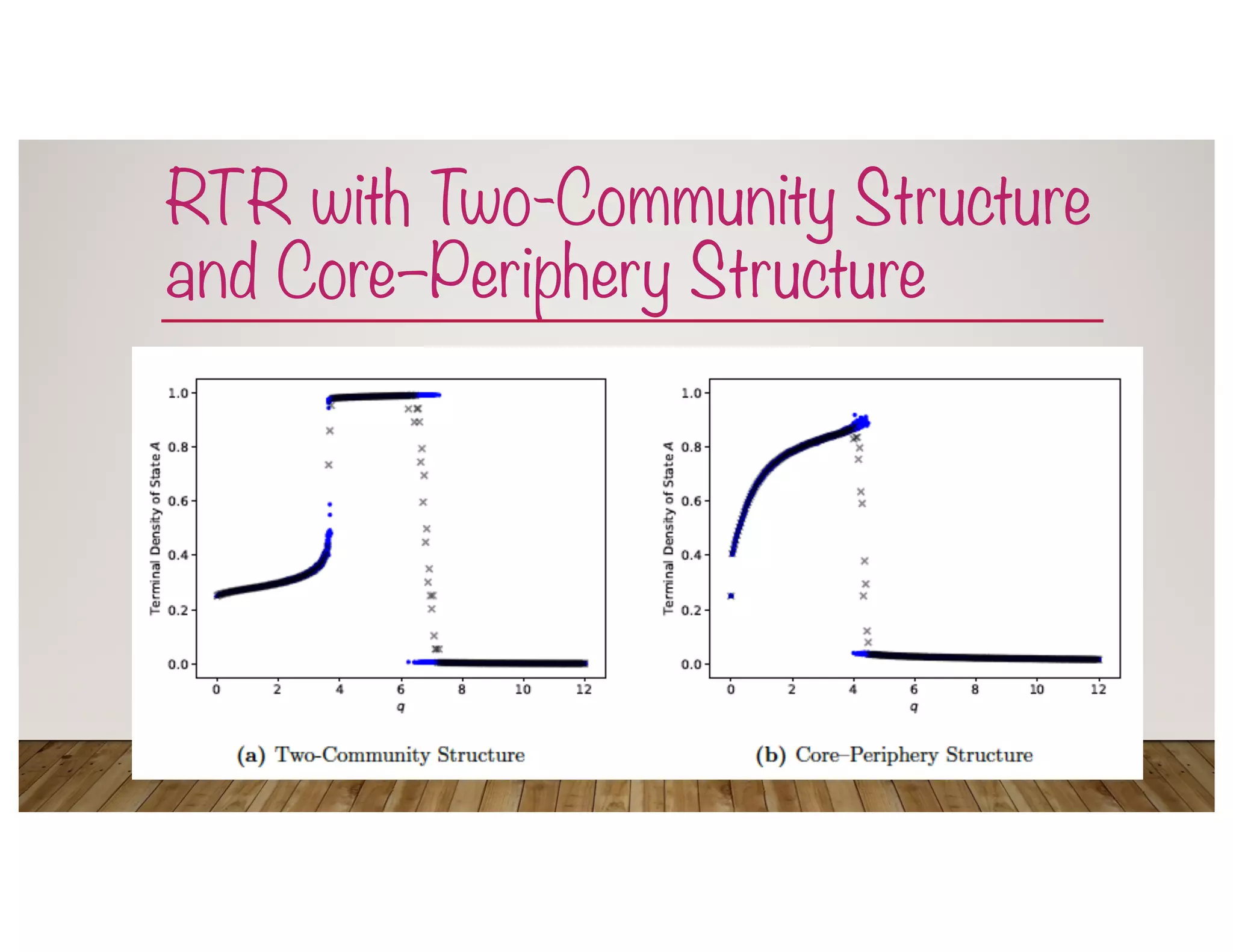
17. A Nonlinear Coevolving Voter Model
• Y. Kureh & MAP [2020], “Fitting In
and Breaking Up: A Nonlinear Version
of Coevolving Voter Models”, Physical
Review E, Vol. 101, No. 6: 062303
• We consider versions of the model with
three types of changes in network
structure.
• Each step: probability !q of rewiring
step and complementary probability 1 –
!q of opinion update
• q = nonlinearity parameter

18. A Schematic of One Step

19. Example: Rewire-to-Random Model
on G(N,p) Erdös–Rényi Networks

20. RTR with Two-Community Structure
and Core–Periphery Structure

21. Majority Illusion and Echo Chambers
• “Liberal Facebook” versus
“Conservative Facebook”:
http://graphics.wsj.com/blue-feed-
red-feed/
• “Majority illusion”: K. Lerman, X.
Yan, & X.-Z. Wu, PLoS ONE, Vol.
11, No. 2: e0147617 2016
• Such network structures form
naturally from homophily and are
exacerbated further by heated
arguments in contentious times.

22. “Majority Illusion” and “Minority
Illusion” in our Coevolving Voter Model

23. Bounded-Confidence Models

24. Bounded-Confidence Models
• Continuous-valued opinions on some space, such as [–1,1]
• When two agents interact:
• If their opinions are sufficiently close, they compromise by some amount
• Otherwise, their opinions don’t change
• Two best-known variants
• Deffuant et al. model: asynchronous updating of node states
• Hegselmann–Krause model: synchronous updating of node states
• Most traditionally studied without network structure (i.e., all-to-all coupling of agents) and with a
view towards studying consensus
• By contrast, original motivation — but barely explored in practice — of bounded-confidence models
was to examine how extremist ideas, even when seeded in a small proportion of a population, can take
root in a population

25. Bounded-Confidence Model on Networks
• X. Flora Meng, Robert A. Van Gorder, & MAP [2018], “Opinion Formation and Distribution in a Bounded-
Confidence Model on Various Networks”, Physical Review E, Vol. 97, No. 2: 022312
• Network structure has a major effect on the dynamics, including how many opinion groups form and how long they take to form
• At each discrete time, randomly select a pair of agents who are adjacent in a network
• If their opinions are close enough, they compromise their opinion by an amount proportional to the difference
• If their opinions are too far apart, they don’t change
• Complicated dynamics
• Does consensus occur? How many opinion groups are there at steady state? How long does it take to converge to steady state?
How does this depend on parameters and network structure?
• Example: Convergence time seems to undergo a critical transition with respect to opinion confidence bound (indicating
compromise range) on some types of networks

27. Example: G(N,p) ER Networks

28. Influence of Media
• Heather Z. Brooks & MAP [2020], “A Model for the Influence of Media on the Ideology of
Content in Online Social Networks”, Physical Review Research, Vol. 2, No. 2: 023041)
• Discrete events (sharing stories), but the probability to share them (and thereby influence
opinions of neighboring nodes) is based on a bounded-confidence mechanism
• Distance based both on location in ideology space and on the level of quality of the content that is
being spread
• Include “media nodes” that have only out-edges
• How easily can media nodes with extreme ideological positions influence opinions in a network?
• Future considerations: can also incorporate bots, sockpuppet accounts, etc.

30. Example using Hand-Curated Media
Locations in (Ideology, Quality) Space

31. Conclusions
• Lots of cool stuff to study in opinion and spreading models on networks
• Flavors of models include threshold models, voter models, bounded-confidence models, and others.
• How does network structure affect dynamics?
• Is there a consensus? How many opinion groups? How long does it take to converge to a steady state? Etc.
• Some very recent and upcoming papers
• A. Hickok, Y. H. Kureh, H. Z. Brooks, M. Feng, & MAP: “A Bounded-Confidence Model of Opinion
Dynamics on Hypergraphs”, arXiv:2104.00720
• H. Z. Brooks & MAP, “Spreading Cascades in Bounded-Confidence Dynamics on Networks”, in preparation
• M. Feng, H. Z. Brooks, Y. H. Kureh, A. Hickok, & MAP: “A Bounded-Confidence Model of Opinion
Dynamics on Multilayer Networks”
• U. Kanjanasaratool, M. Feng, & MAP: “An Adaptive Bounded-Confidence Model”, in preparation