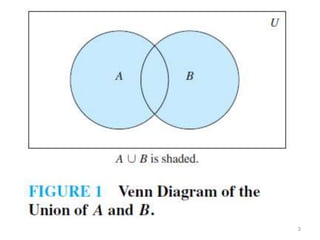
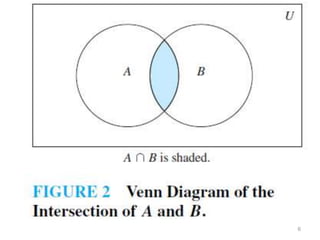
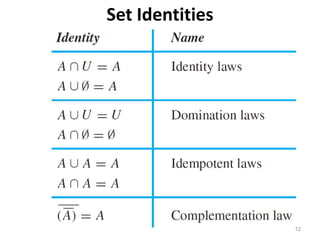
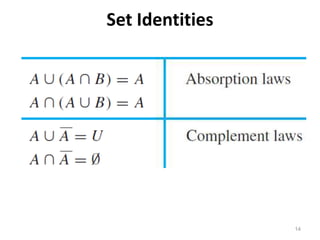
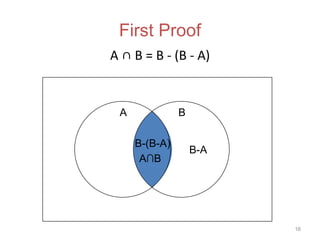
The document discusses set operations such as union, intersection, difference, and complement. It defines each operation formally and provides examples. Properties of each operation are described, such as the commutative, associative, identity and domination laws. Disjoint sets are defined as sets whose intersection is the empty set. The cardinality of the union and intersection of finite sets A and B is discussed. Methods for proving set identities are presented, including using basic set identities, subset proofs, and set builder notation.

1. CSC102 - Discrete Structures
(Discrete Mathematics)
Set Operations

2. Set operations: Union
Formal definition for the union of two sets:
A U B = { x | x  A or x  B } or
A U B = { x  U| x  A or x  B }
Further examples
 {1, 2, 3}  {3, 4, 5} = {1, 2, 3, 4, 5}
 {a, b}  {3, 4} = {a, b, 3, 4}
 {1, 2}   = {1, 2}
Properties of the union operation
 A   = A Identity law
 A  U = U Domination law
 A  A = A Idempotent law
 A  B = B  A Commutative law
 A  (B  C) = (A  B)  C Associative law
2

3. 3

4. Set presentation
4

5. Set operations: Intersection
Formal definition for the intersection of two sets:
A ∩ B = { x | x  A and x  B }
Examples
 {1, 2, 3} ∩ {3, 4, 5} = {3}
 {a, b} ∩ {3, 4} = 
 {1, 2} ∩  = 
Properties of the intersection operation
 A ∩ U = A Identity law
 A ∩  =  Domination law
 A ∩ A = A Idempotent law
 A ∩ B = B ∩ A Commutative law
 A ∩ (B ∩ C) = (A ∩ B) ∩ C Associative law
5

6. 6

7. Disjoint sets
Formal definition for disjoint sets:
Two sets are disjoint if their intersection is the
empty set
Further examples
 {1, 2, 3} and {3, 4, 5} are not disjoint
 {a, b} and {3, 4} are disjoint
 {1, 2} and  are disjoint
• Their intersection is the empty set
  and  are disjoint!
• Because their intersection is the empty set
7

8. Exercise
• What is the cardinality of AUB where A and B
are two finite sets?
• |A ∪ B| = |A| + |B| ???
• Incorrect
• |A ∪ B| = |A| + |B| − |A ∩ B|???
• Correct
8

9. Set operations: Difference
Formal definition for the difference of two sets:
A - B = { x | x  A and x  B }
Sometimes denoted by AB.
Further examples
 {1, 2, 3} - {3, 4, 5} = {1, 2}
 {a, b} - {3, 4} = {a, b}
 {1, 2} -  = {1, 2}
The difference of any set S with the empty set will be the set S
9

10. Exercise
• What is the cardinality of A∩B where A and B
are two finite sets?
• |A∩B | = |B| - |B - A|???
• Correct
• |A∩B | = |A| - |A - B|???
• Correct
• |A∩B | = |A| + |B| - (|A - B| + |B - A|)???
• Incorrect
10

11. Complement sets
Formal definition for the complement of a set:
A = { x | x  A } = Ac
 Or U – A, where U is the universal set
Further examples (assuming U = Z)
 {1, 2, 3}c = { …, -2, -1, 0, 4, 5, 6, … }
 {a, b}c = Z
Properties of complement sets
 (Ac)c = A Complementation law
 A  Ac = U Complement law
 A ∩ Ac =  Complement law
11

12. Set Identities
12

13. Set Identities
13

14. Set Identities
14

15. How to prove a set identity
For example: A ∩ B = B - (B - A)
Four methods:
1. Using the basic set identities
2. Proving that each set is a subset of each other
3. Using set builder notation and logical
equivalences
4. Using membership tables (we’ll not study it)
• Similar to truth tables
15

16. First Proof
A ∩ B = B - (B - A)
A B
A∩B
B-A
B-(B-A)
16

17. 1. Proof by Set Identities
A  B = A - (A - B) = B – (B – A)
Proof: A - (A - B)
= A - (A  Bc) A - B = A  Bc
= A  (A  Bc)c Same as above
= A  (Ac  B) De Morgan’s Law
= (A  Ac)  (A  B) Distributive Law
=   (A  B) Complement Law
= A  B Identity Law
17

18. 2. Showing each is a subset of the others
Second Example Proof
 (A  B)c = Ac  Bc
Proof: Want to prove that
(A  B)c  Ac  Bc and Ac  Bc  (A  B)c
(i) x  (A  B)c
 x  (A  B)
  (x  A  B)
  (x  A  x  B)
  (x  A)   (x  B)
 x  A  x  B
 x  Ac  x  Bc
 x  Ac  Bc
(ii) Similarly we show that Ac  Bc  (A  B)c
18

19. Same proof with Set builder Notation
(A ∩ B)c = Ac ∪ Bc
• (A ∩ B)c = {x | x  A ∩ B} Definition of complement
= {x |￢(x ∈ (A ∩ B))} Definition of does not belong symbol
= {x |￢(x ∈ A ∧ x ∈ B)} Definition of intersection
= {x | ￢(x ∈ A)∨￢(x ∈ B)} De Morgan’s law
= {x | x  A ∨ x  B} Definition of does not belong symbol
= {x | x ∈ Ac ∨ x ∈ Bc} Definition of complement
= {x | x ∈ Ac ∪ Bc} Definition of union
= Ac ∪ Bc meaning of set builder notation
19

20. 20

21. END
21