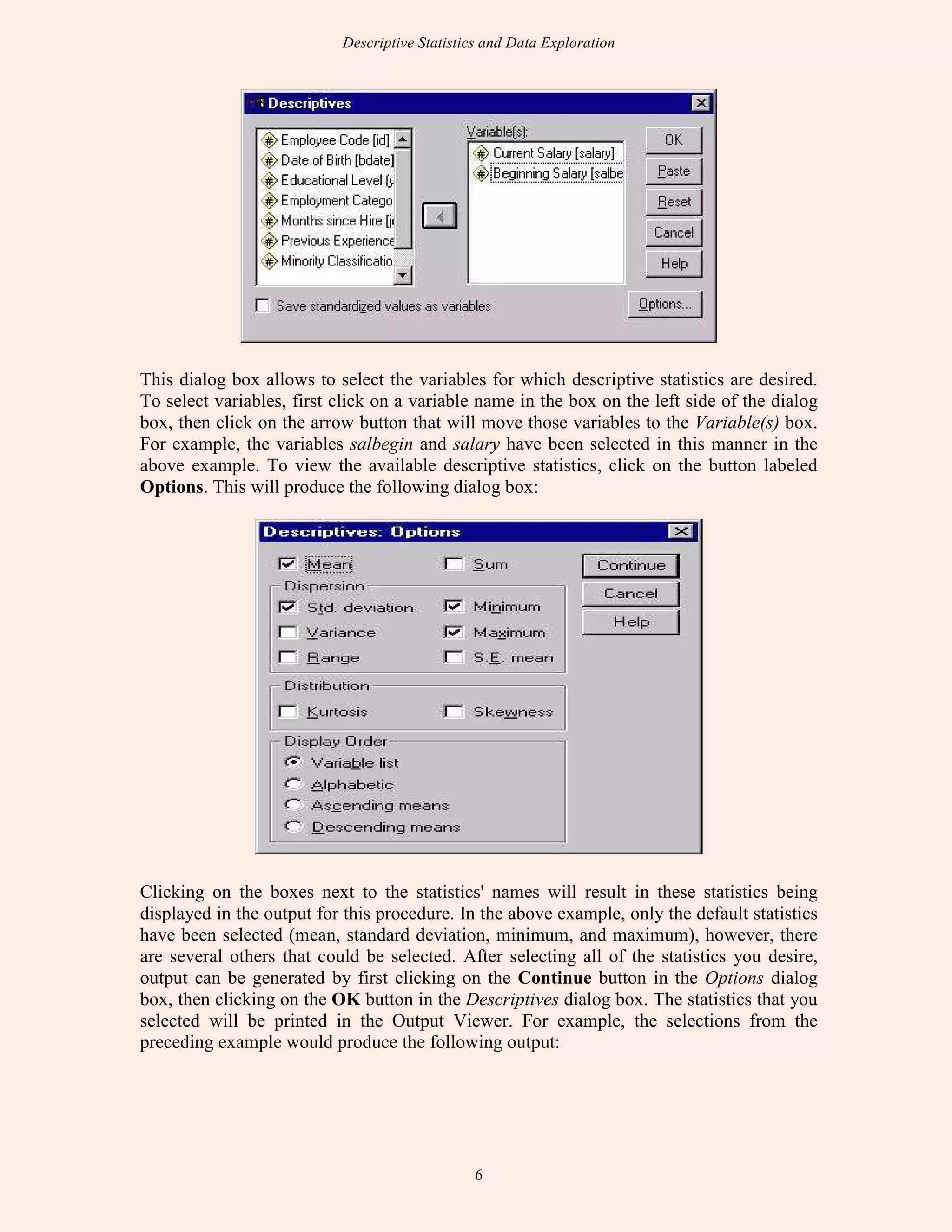
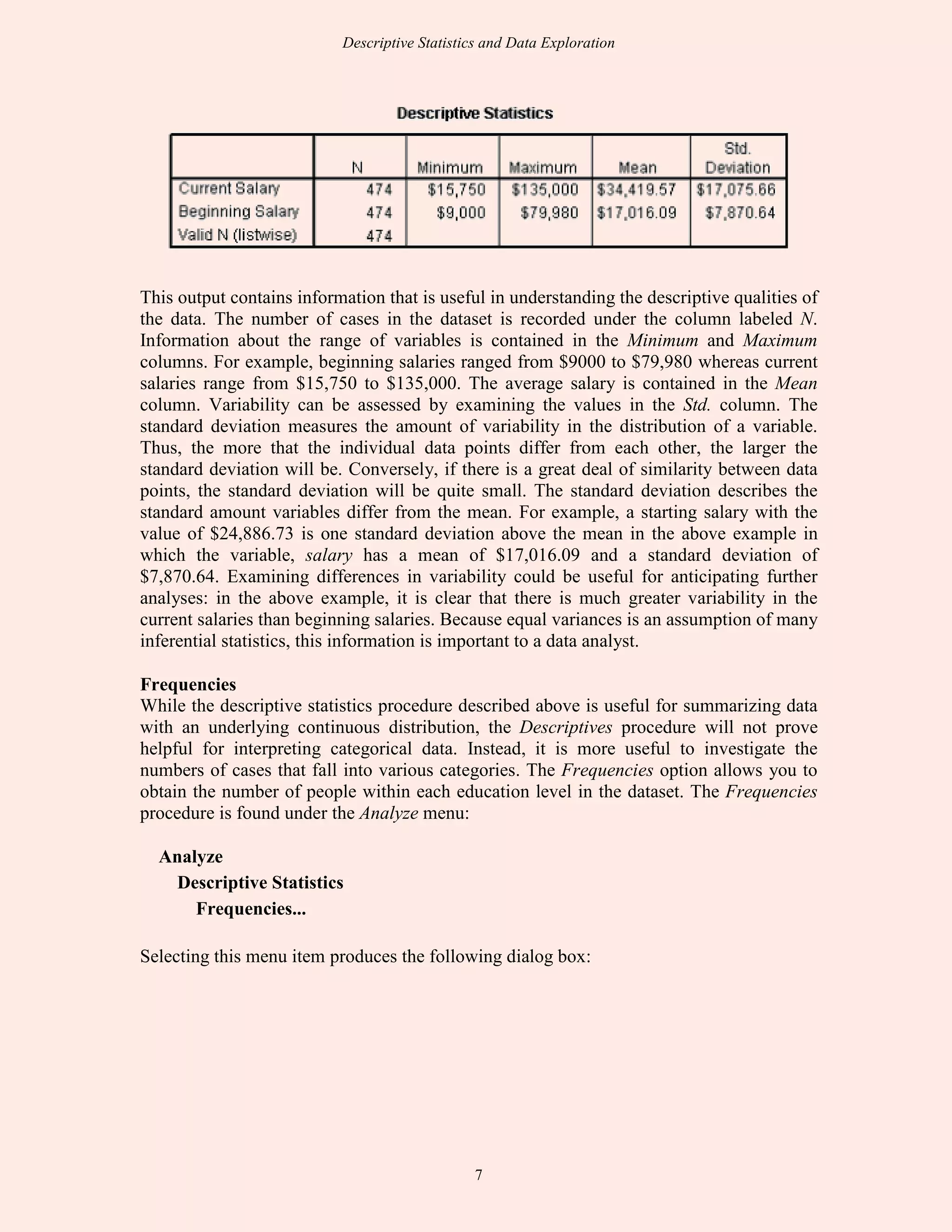
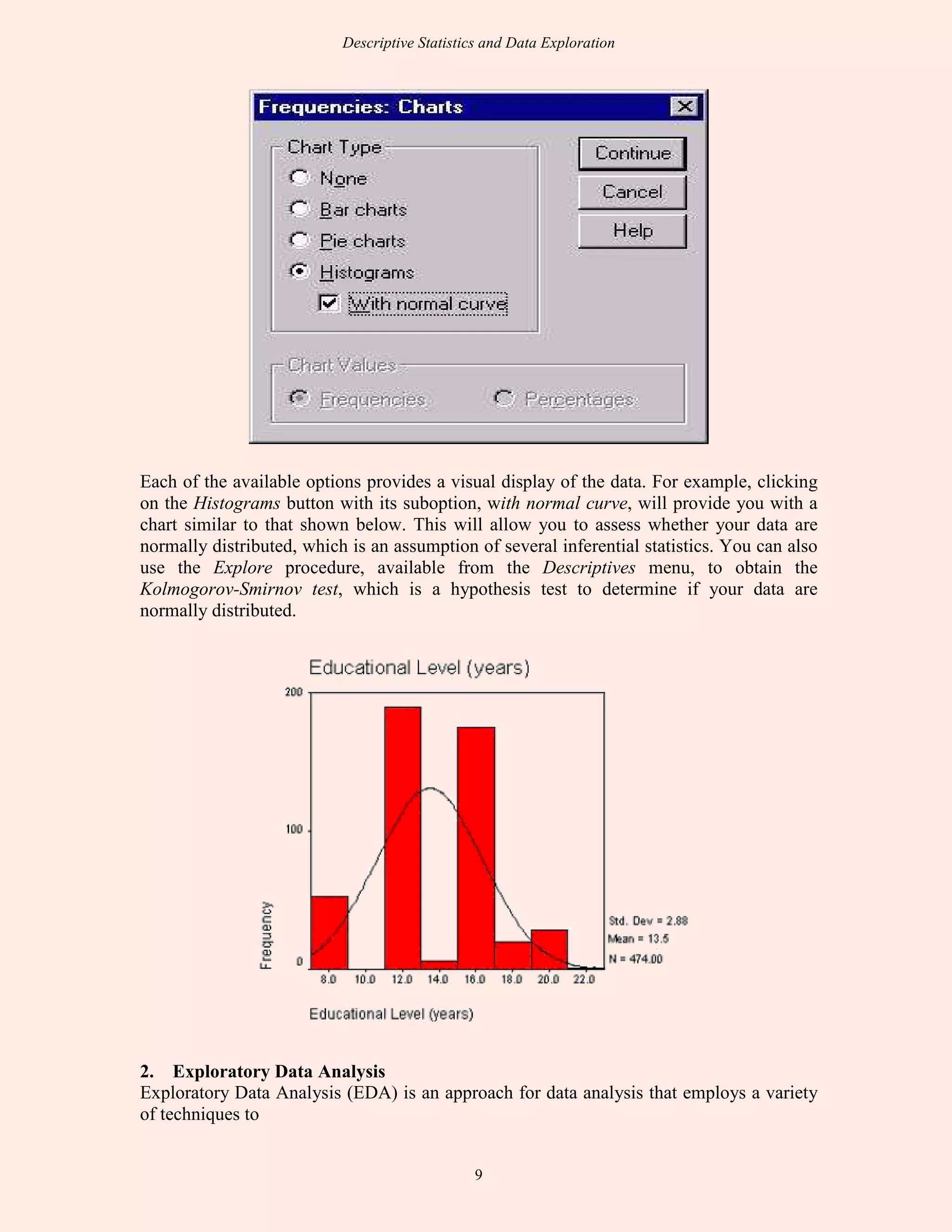
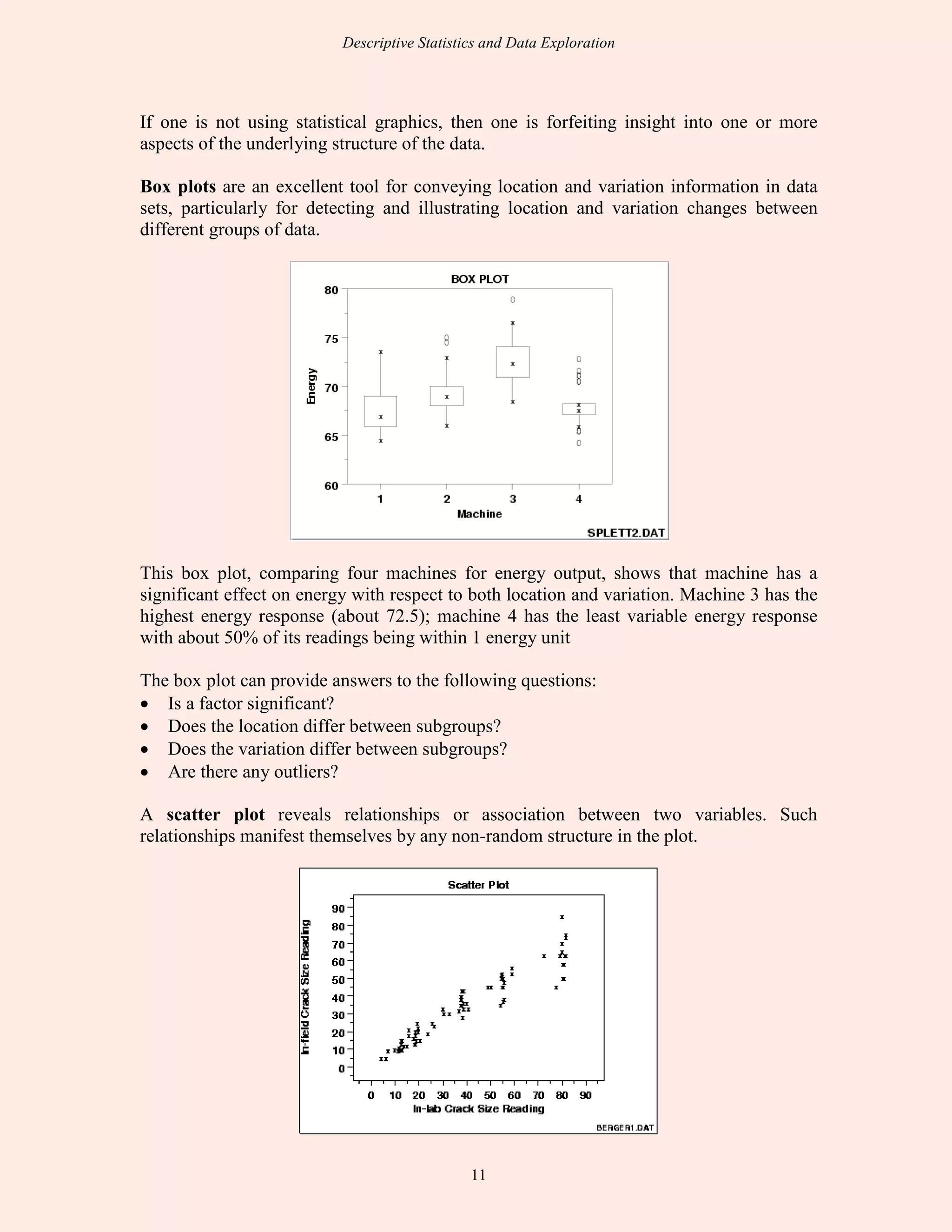
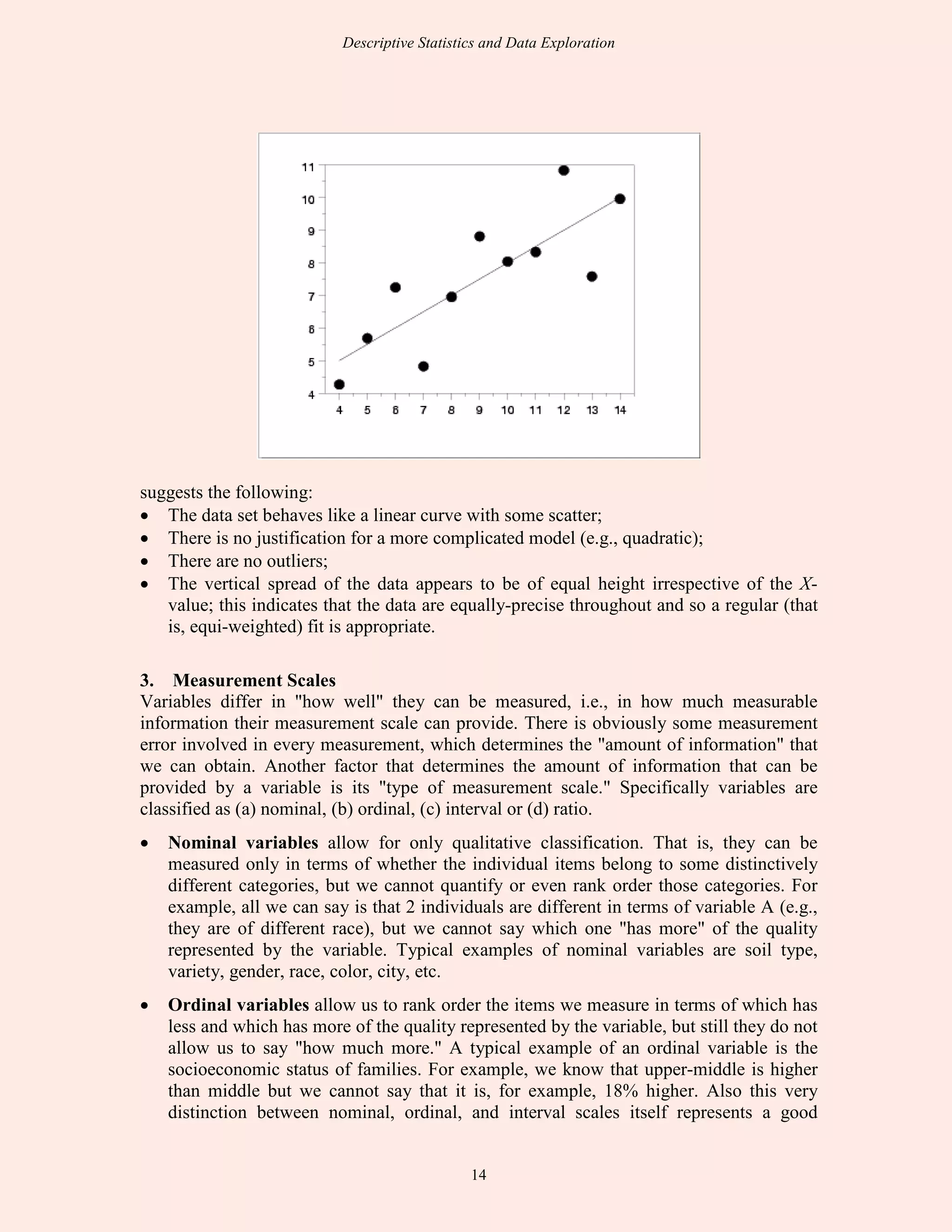
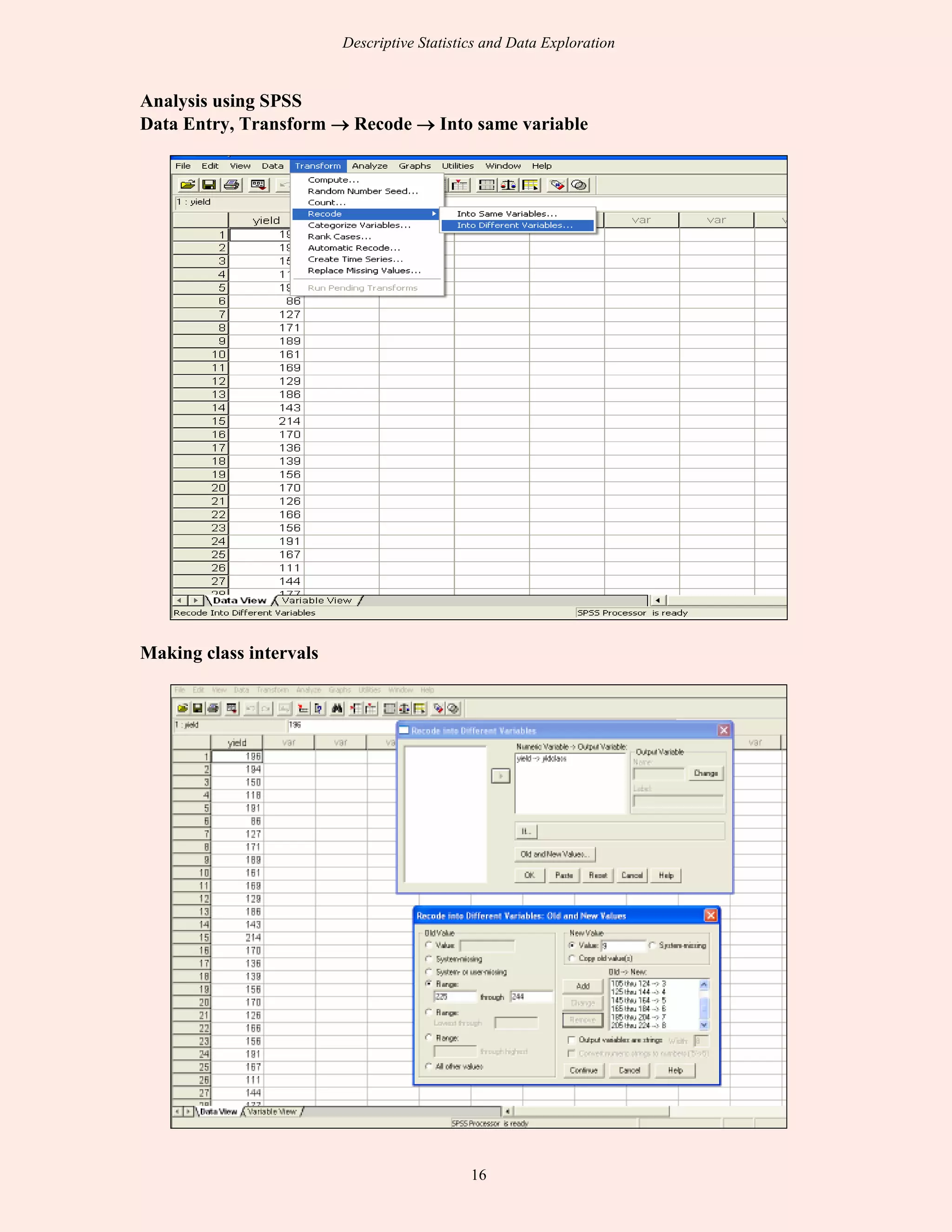
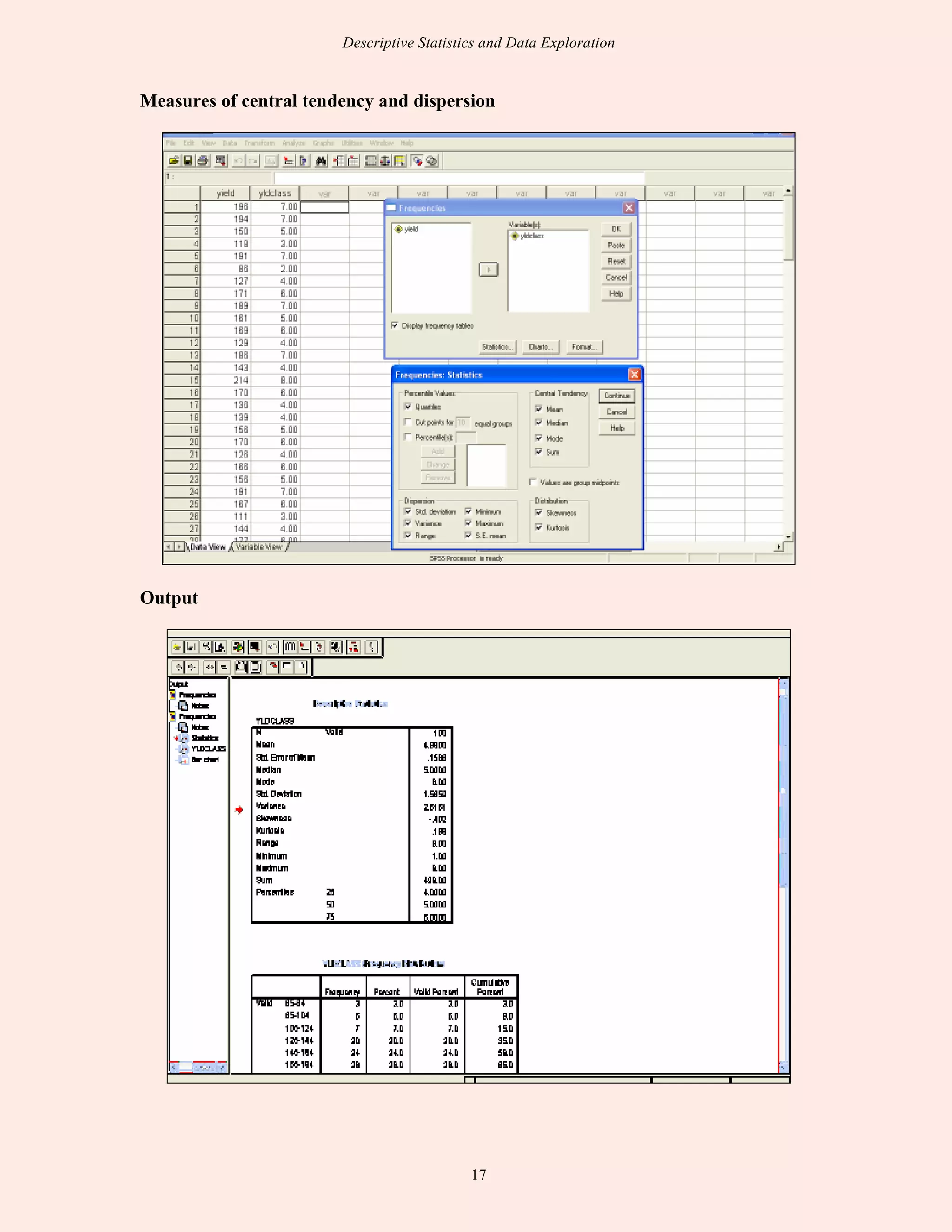
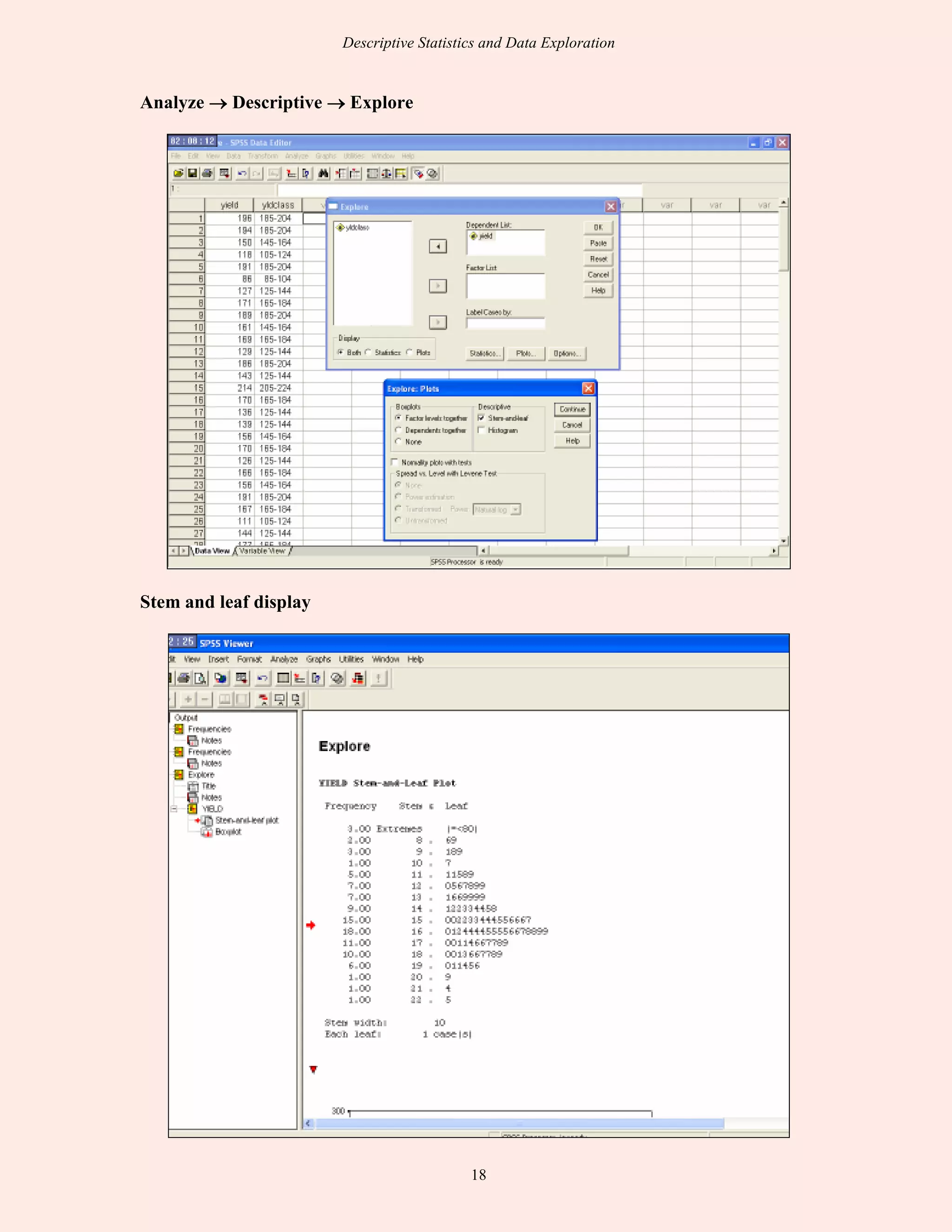
This document discusses descriptive statistics and exploratory data analysis. It defines descriptive statistics as procedures for summarizing quantitative data in a clear way, while exploratory data analysis involves examining data to understand its characteristics. The document outlines common descriptive statistics like the mean, median, mode, standard deviation, and frequency distributions. It also discusses examining distributions, central tendency, dispersion, and using SPSS to calculate descriptive statistics.